Standard deviation

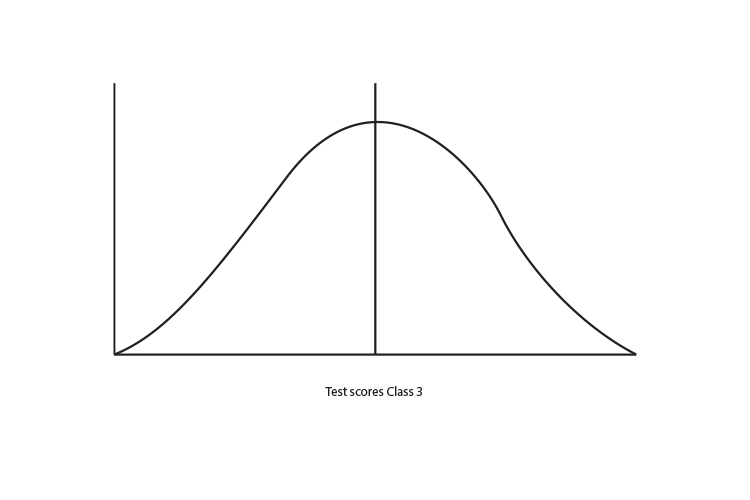
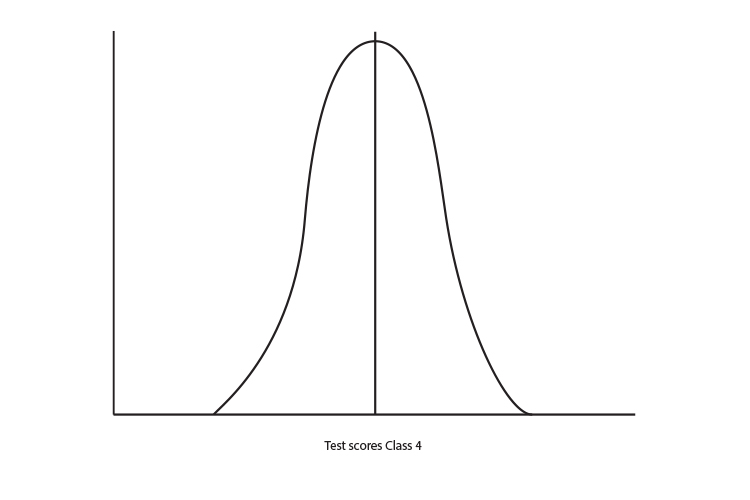
The graph below shows a thousand students taking a test in Class 3 and Class 4. You can see nearly 150 students got a score of between 80 and 90 marks in Class 3. In class 4 nearly 250 students got a score between 80 and 90.

Lets look at the mean (add up all the numbers and divide by the number of numbers) of the following graph.

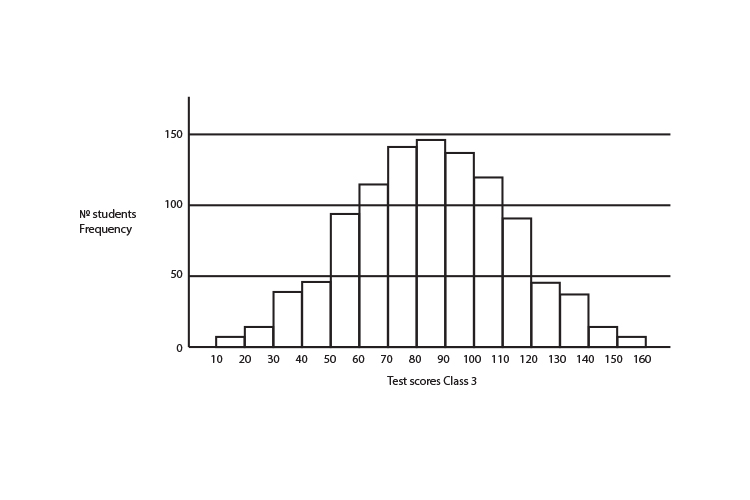
An example of students in class 3 got on an exam

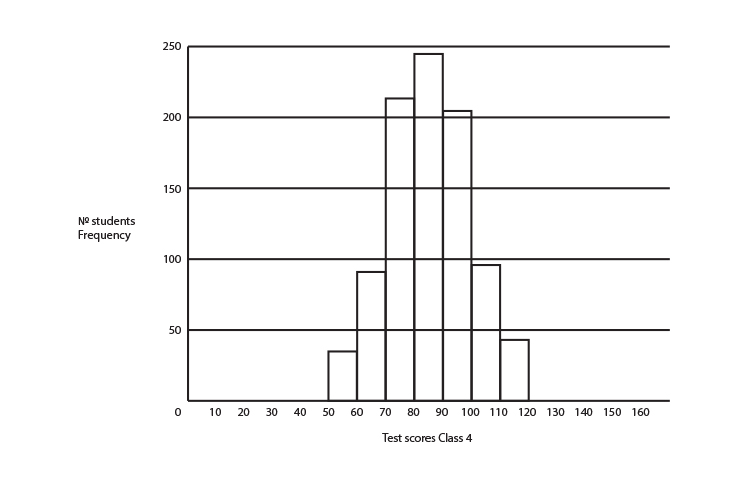The mean or middle of the graph separated The mean of the test scores for year 3 is 85 and the mean of the test scores of year 4 are also 85.

The graphs have the same mean value but very different distributions.

One way to show the differences in these graphs non graphically is to give you a number that tells you how far away 68% of all the data is from the mean (called 1 standard deviation).

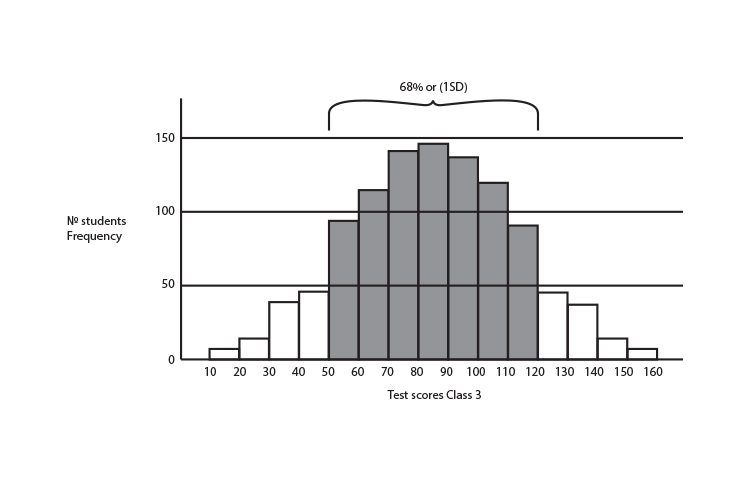
The 1SD of class 3 is between 50 and 120

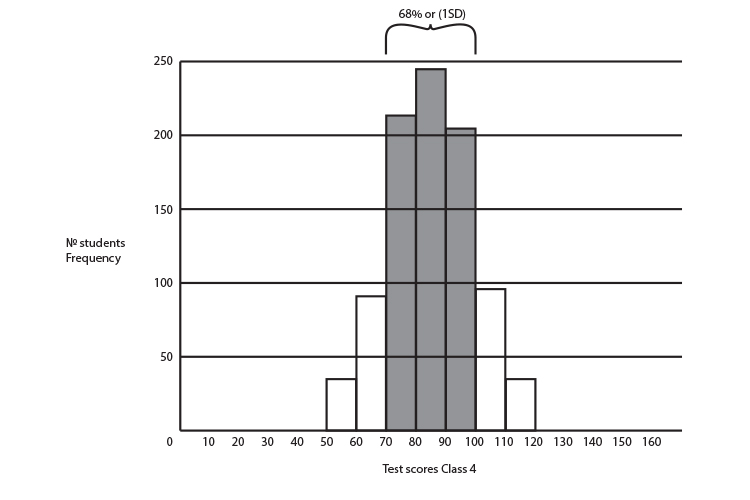
The 1SD of class 4 is between 70 and 100

This only works for graphs that have the shape of a bell, or a bell curve.

Normal distribution where measurements tend to cluster around the mean

The mathematical name for this bell curve is "normal distribution" where the measurements tend to cluster around the mean and tapper off at the edges.

So the curve of the two graphs above would look like:

Normal distribution of class 3

Normal distribution of class 4

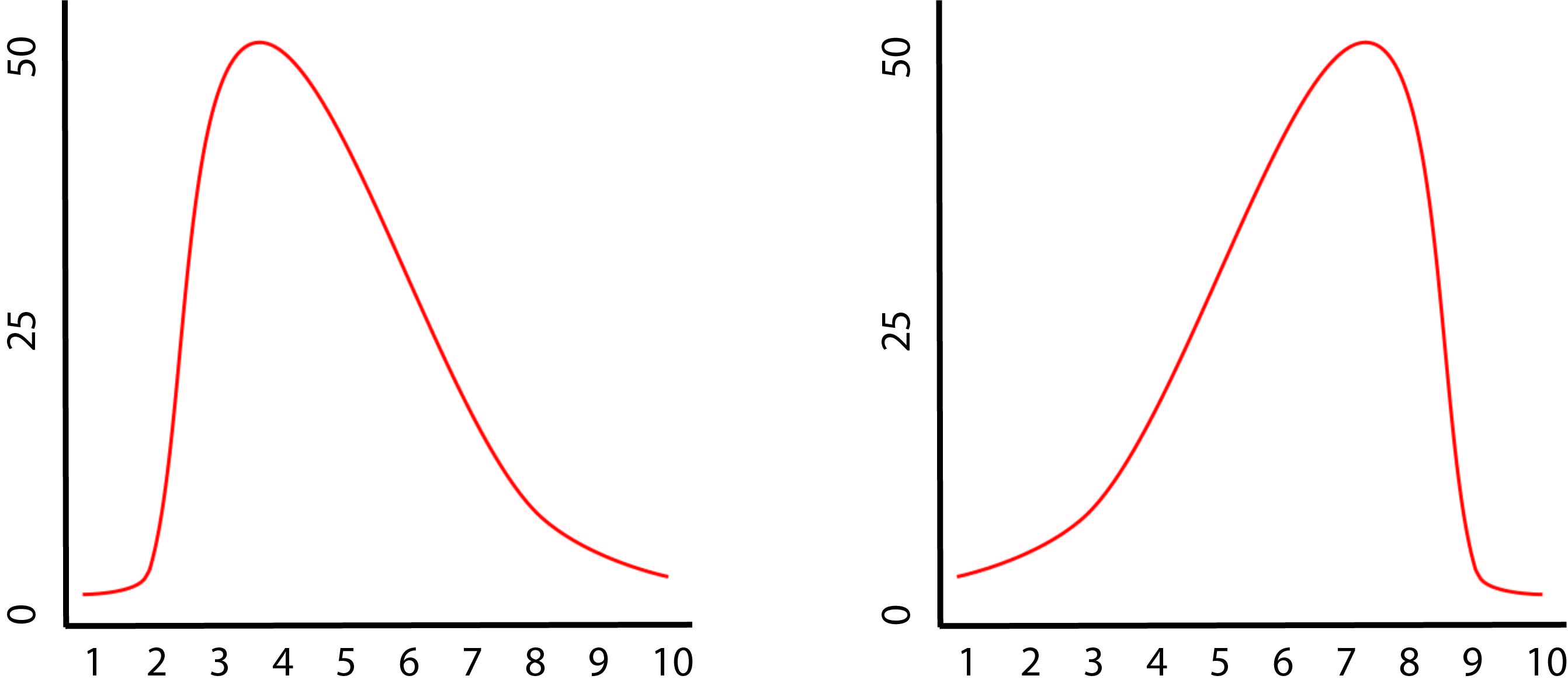
This form of expression using the words "standard deviation" only works for this normal distribution or bell curve. It would not work for any curve that was skewed as:

Standard deviation works only with a bell curve, if the curve is skewed it will not work

Or

Standard deviation wont work on this example

So taking the two graphs above and expressing them as a curve:

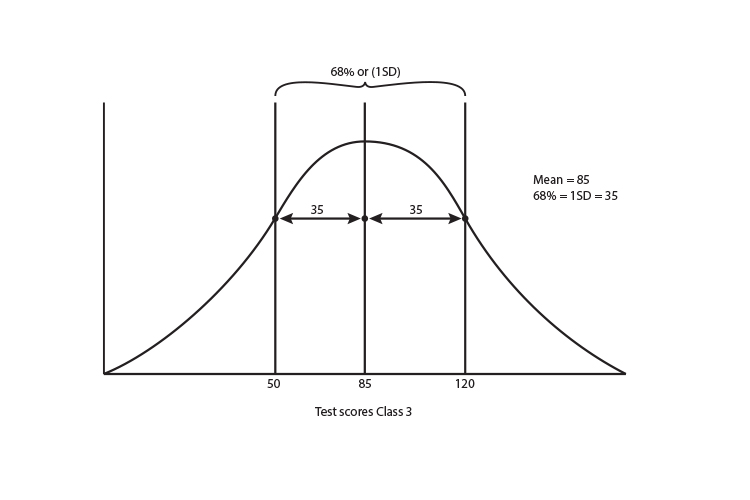
The 68% (1 standard deviation) of Class 3 = 35

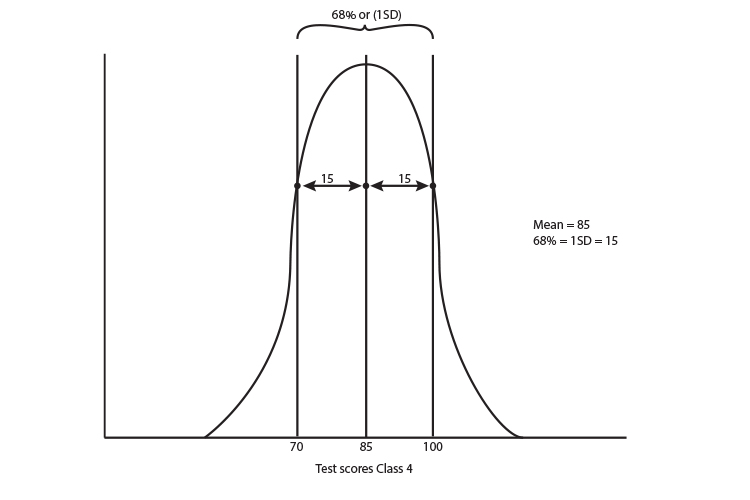
The 68% (1 standard deviation) of Class 4 = 15

As follows graphically:

If you half the mean the answer in this example will be 35

So if you compare

Class 3 mean = 85 and 1 SD (standard deviation) = 35

Class 4 mean = 85 and 1 SD (standard deviation) = 15

You can tell just from the numbers that class 4 has a much more concentrated cluster around the middle than class 3.

The teacher in class 3 may need some extra help for the wide spread of distribution of kids in her class.

More help may be needed for the not-so-highly scoring kids and even more help perhaps for the really smart kids who need extra help to push them on. The graph is so diverse they certainly can't be taught in the same way. Whereas with class 4, the teacher may have a better chance to bring all the kids through together.

All this just from the numbers.