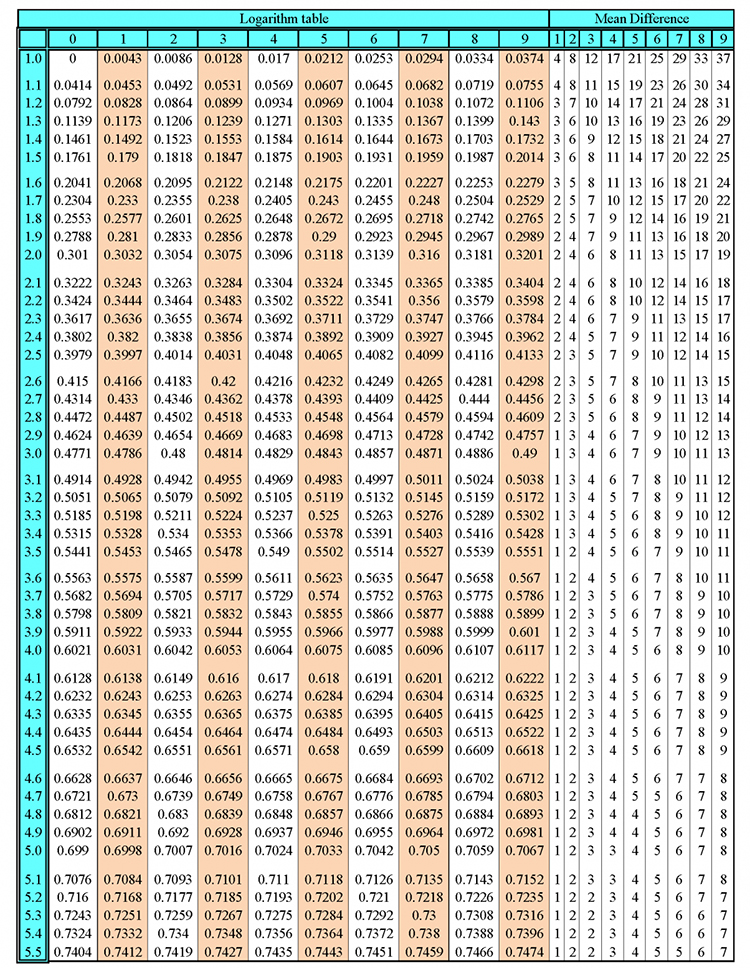
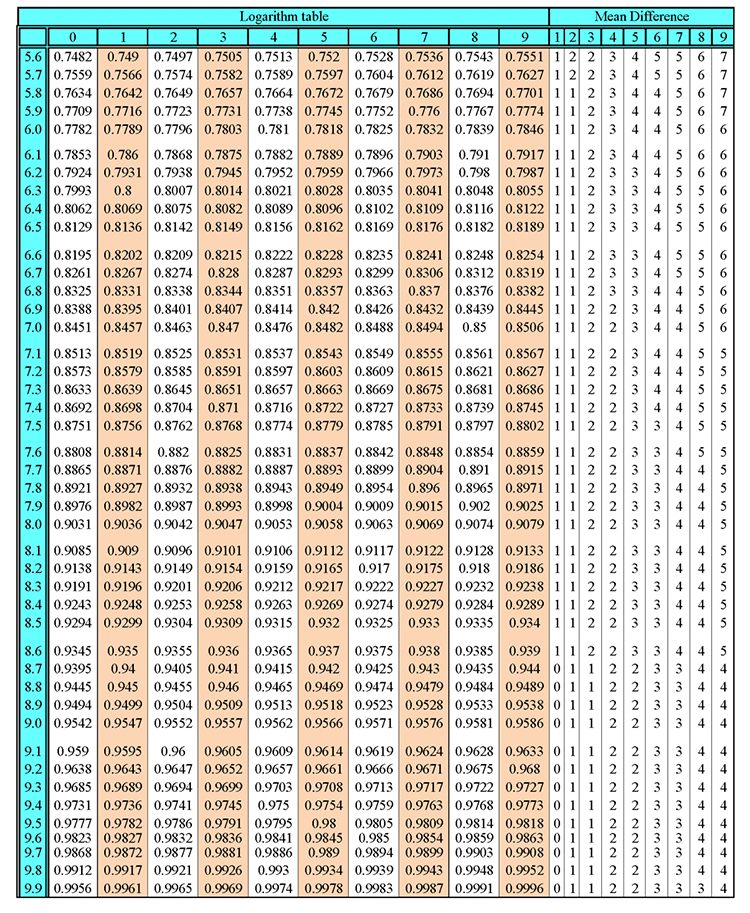
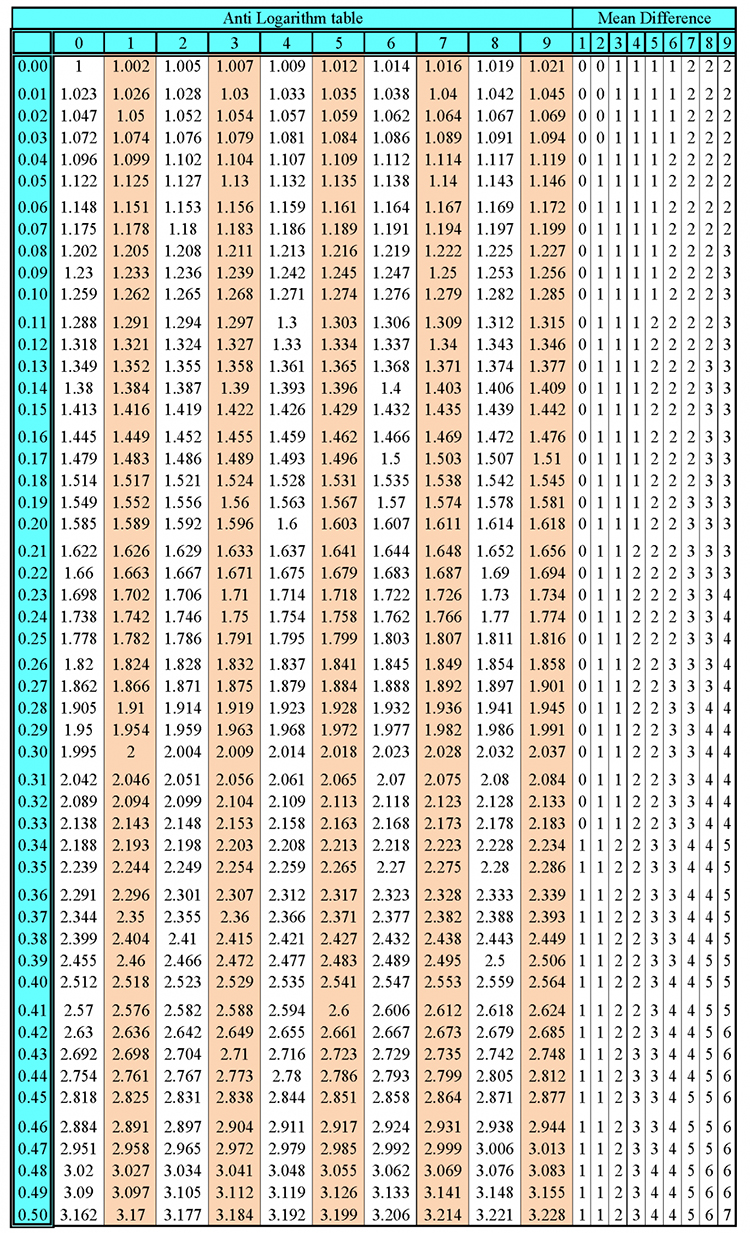
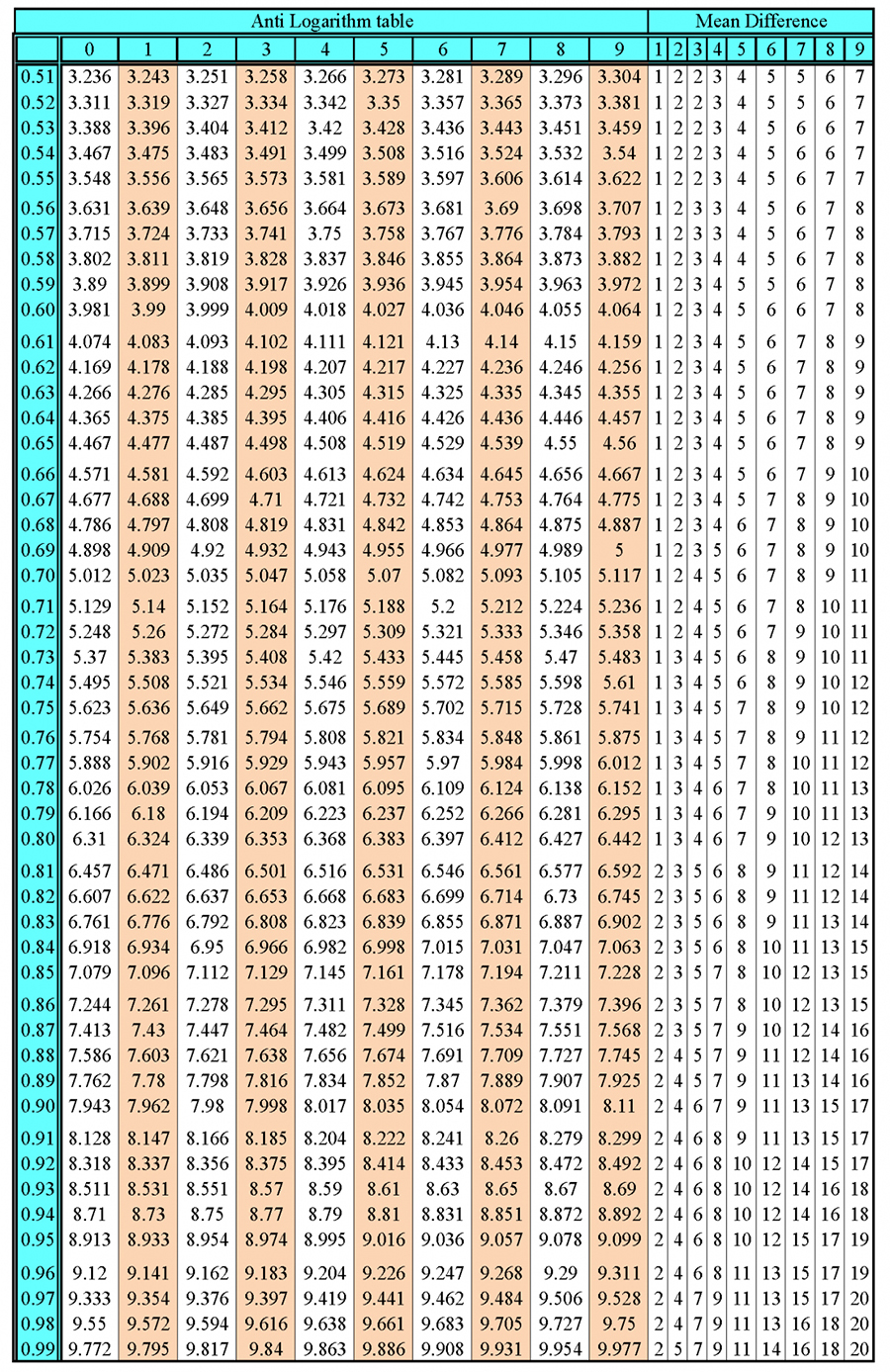
Intercept and midpoint theorem

Thales' intercept theorem

Thales' intercept theorem (or triangular proportionality theorem).

Thales was a Greek mathematician who founded geometry. His name is pronounced "they-leez".

Thales was a Greek mathematician who founded geometry

He had a strange tail (Thales) and raked up hay and leaves (Thales) with it into separate (intercept) piles.

Thales lived in Greece in 640BC and was asked to measure the height of the oldest and largest pyramid in Egypt.

In 640BC Thales lived in Greece, he was asked to measure the oldest pyramid in Egypt

The oldest and largest pyramid in Egypt is the Cheops Pyramid (Cheops is pronounced chee-ops).

By chopping the pyramid in half it would make it very easy to measure but he couldn’t

Now if he could have chopped (Cheops) the pyramid in half it would have been very easy for him to measure the pyramid.

His method was ingenious.

Ingeniously he measured the pyramids shadow only when his own shadow was the same height as himself

To determine the height of the pyramid he measured the length of the pyramid's shadow when the length of his own shadow was equal to his height.

But he played around with these ideas and realised that he could work out the height of the pyramid at any time of the day (he started using poles as well).

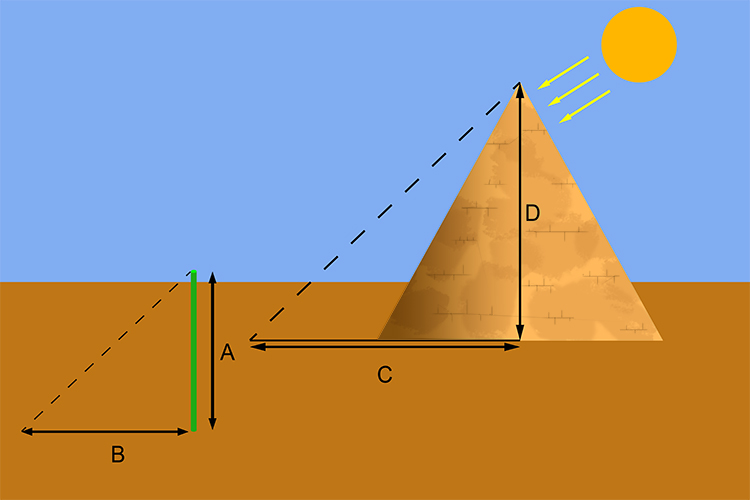
Thales found it could work at any time of day so he started to use poles he would measure the height and shadow of the pole also measuring the length of the shadow of the pyramid realising the intercept ratio

Thales measured the length of a pole (A) and the length of its shadow (B) and at the same time measured the length of the shadow C.

He realised that the ratio

`A/B` is identical to `D/C`

And therefore `A/B=D/C`

So if A = 1.8m B = 2.2m and C = 168m then:

`1.8/2.2=D/168`

`D=1.8/2.2times168`

Therefore D = 138metres

So at any time of day Thales could have worked out the height of the Pyramid.