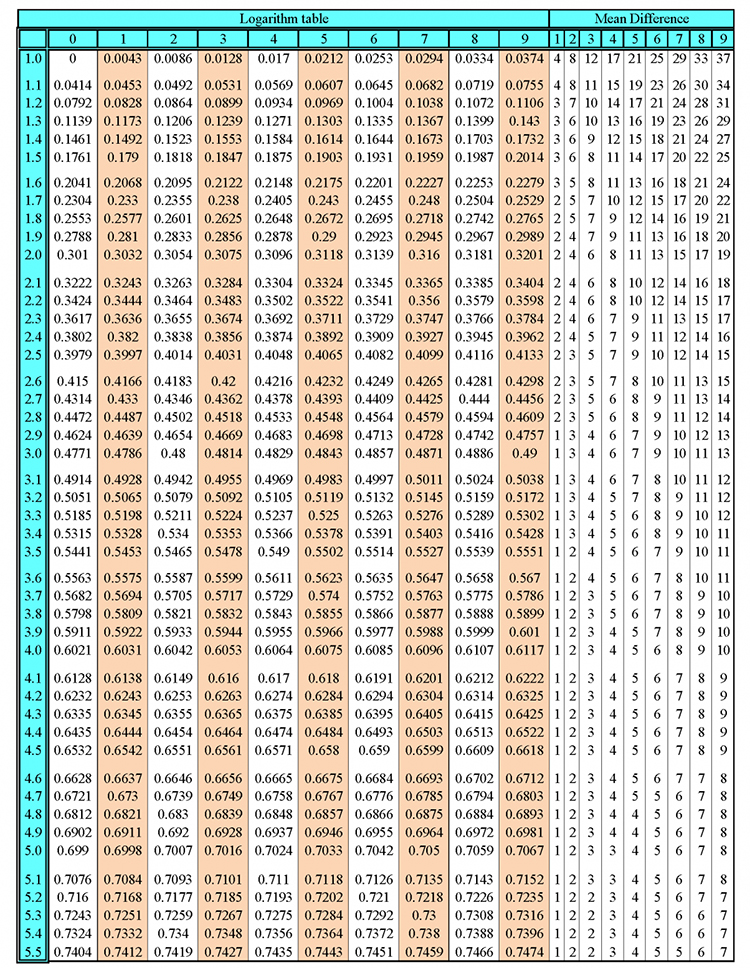
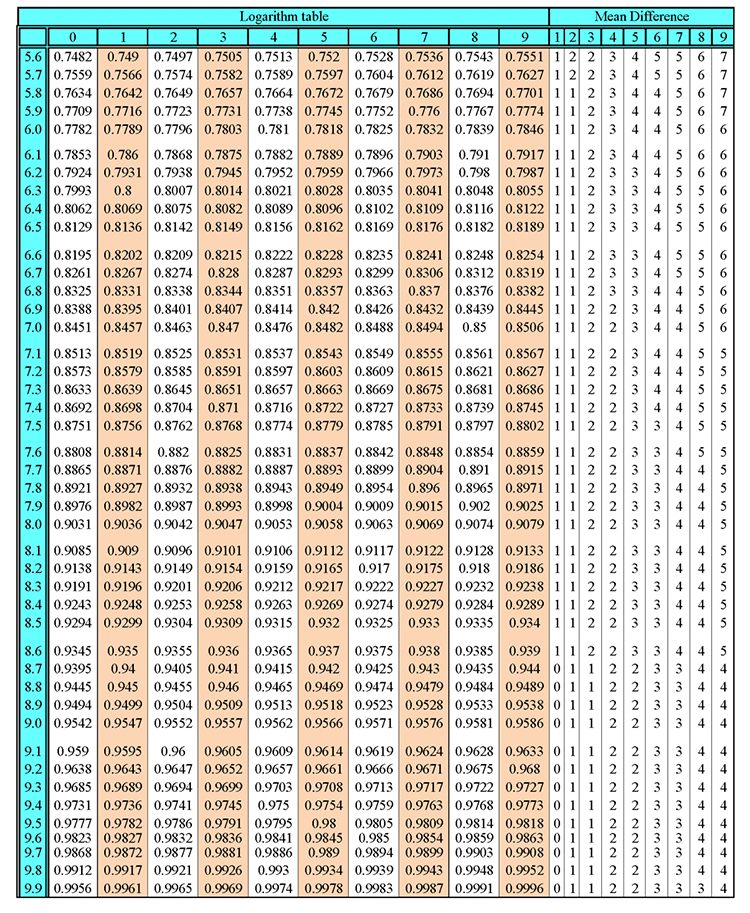
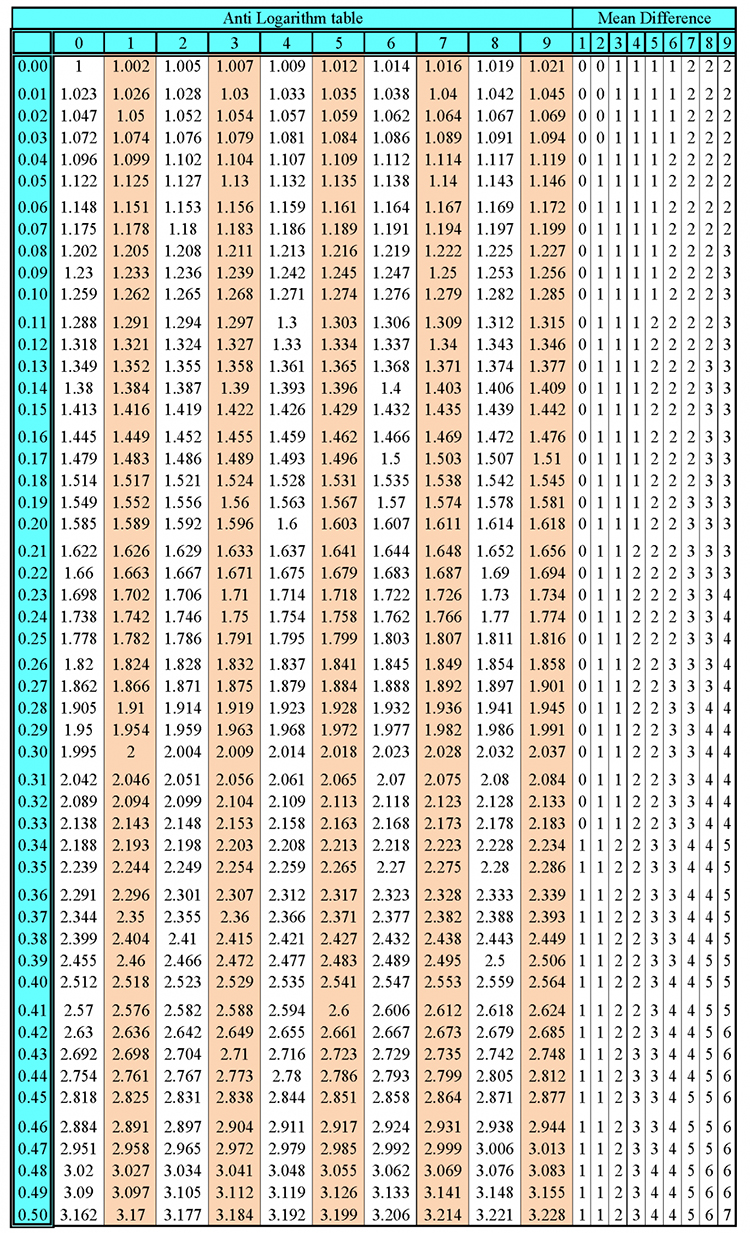
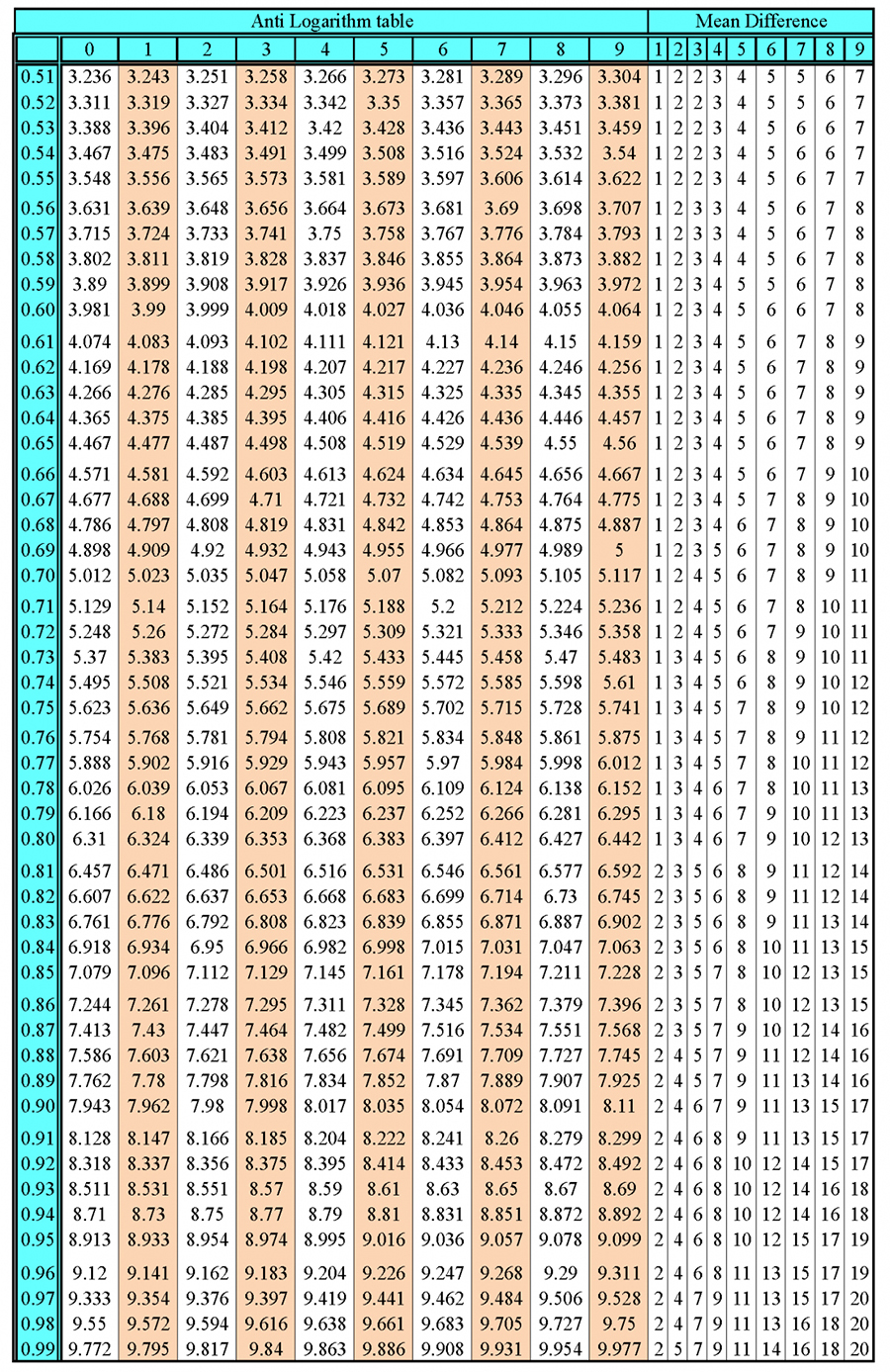
introduction

It's important to remember that starting with 30° and a right angled triangle the ratio of the length of the sides are:

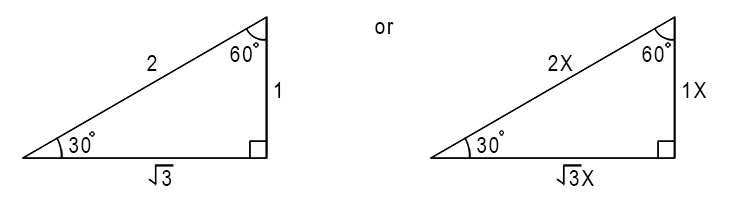
This 30 - 60 - 90 triangle ratio rule will allow you to solve many trigonometry problems without either the need for a calculator or the need to approximate your answers. For example from the triangle above we can see that:

Sine of 30° = `(O)/(H)=(1)/(2)`

Cosine of 60° = `(A)/(H)=(1)/(2)`

Or other examples include:

Tan 30 = `(O)/(A)=1/(root()3)`

Tan 60 = `(O)/(A)=root()3/(1)=root()3`

It's also important to remember that starting with 45° and a right angled triangle the ratio of the length of the sides are:

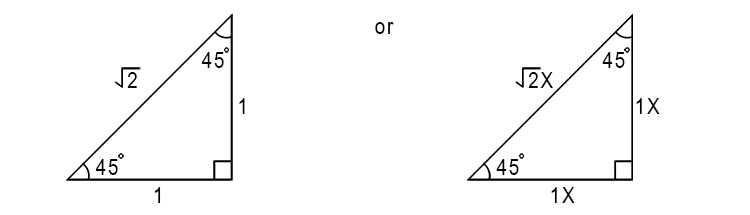
This 45 - 90 - 45 triangle ratio rule will allow you to solve many trigonometry problems without the need for a calculator or the need to approximate your answers. For example from the triangle above we can see that:

Tan 45° = `(O)/(A)=(1)/(1)=1`

Sin 45° = `(O)/(H)=(1)/(root()2)`

Cos 45° = `(A)/(H)=(1)/(root()2)`