Parallel Resistance Water Analogy
To the picture of the tank on the first page, we will now add lots of pipes to the underside of the tank.
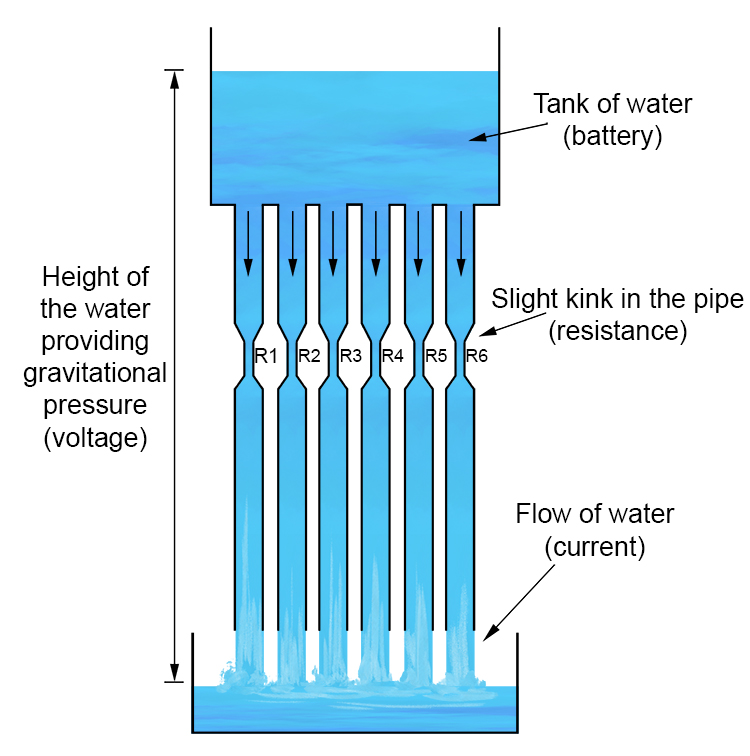
This example diagram provides a visual explanation of the rules you need to remember parallel resistance.
1/ The voltage is the same across all components (resistances).
In the series resistance (kinks in the pipes) the voltage was shared between the components (resistances).
In parallel circuits, every single component (resistances) gets the full, maximum voltage.
Therefore bulbs in parallel have the same brightness (assuming equal resistance).
(Note: The head of tank water will be used up quicker the more bulbs in parallel are added (the battery will be used up more quickly)).
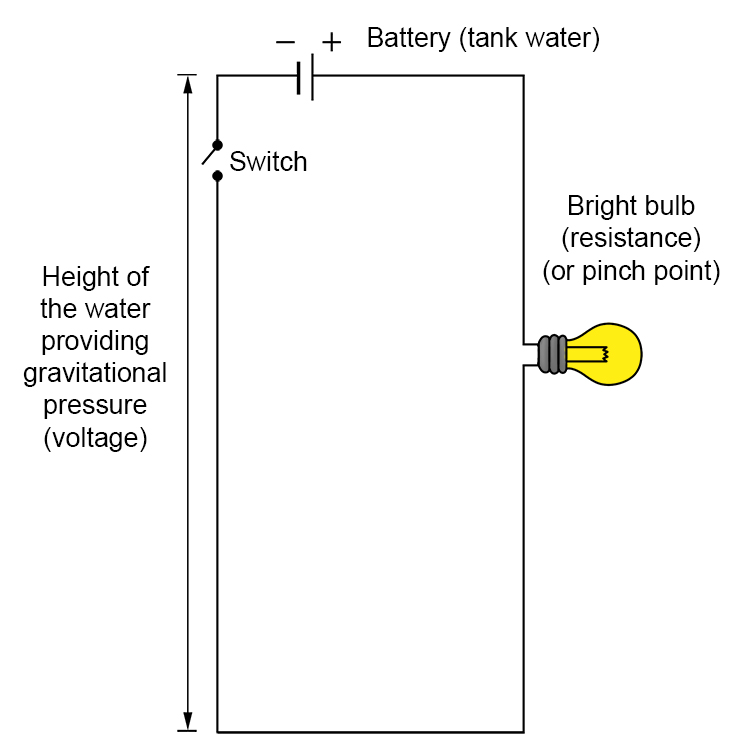
Adding another light bulb in parallel.
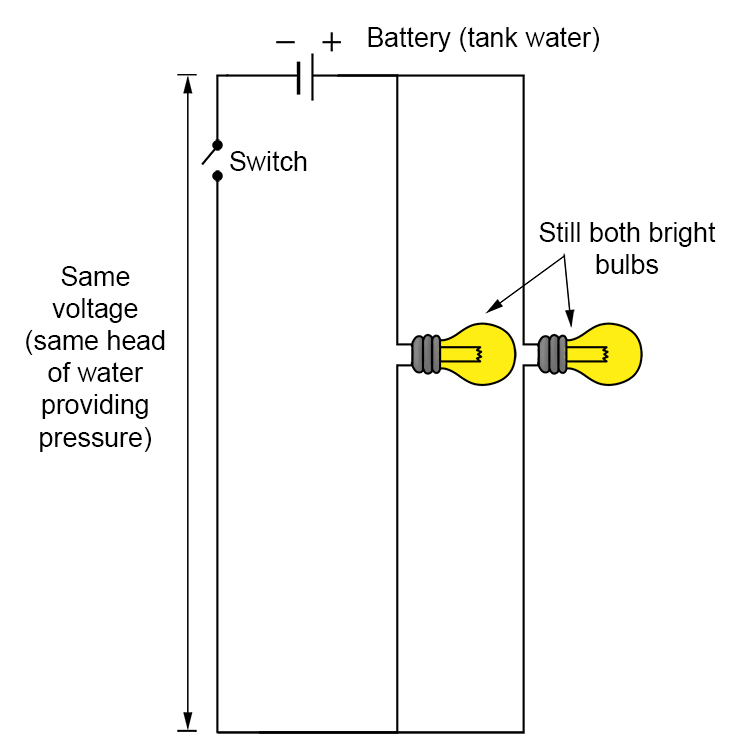
2/ Adding more light bulbs (resistance) in parallel actually increases the current flow.
The current increases if you add wires with some resistance in parallel (light bulbs)
| Because in parallel | \frac{1}{R_T} | = | \frac{1}{R_1}+\frac{1}{R_2} | |
| then | V | = | IR_{Total} | |
| and current | I | = | \frac{V}{R_T} | ← Keep overall voltage (water gravity height pressure) the same |
Example
I=\frac{V}{R_T}=\frac{5volts}{1ohm}=5amps
And now add another wire and light bulb (a kink/resistance) in parallel.
| I | = | \frac{V}{R_T} | = | \frac{5}{\left(\frac{1}{R_T}=\frac{1}{1ohm}+\frac{1}{1ohm}\right)} |
| I | = | \frac{5}{\left(\frac{1}{R_T}=\frac{2}{1}\right)} | ||
| I | = | \frac{5}{\left(R_T=1/2\right)} | ||
| I | = | \frac{5}{\left(\frac{1}{2}\right)} | ||
| I | = | 10amps |
So adding another wire and lamp of the same resistance has increased the current from 5amps to 10amps. The voltage has remained the same.
3/ The sum of the currents is equal to the total current.
If you have lots of light bulbs in parallel and you know the current through each circuit, just add them up.
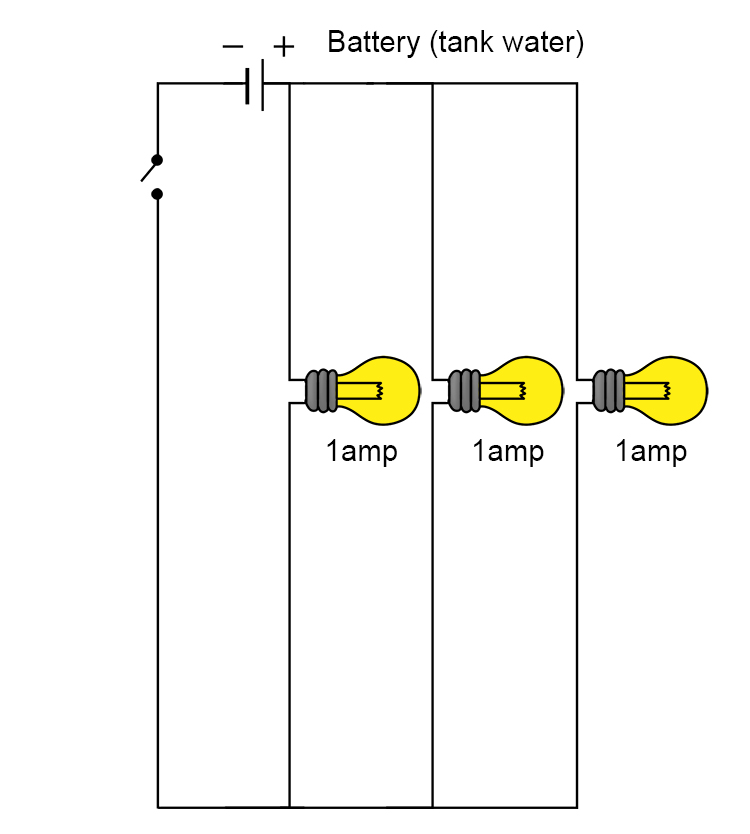
| Total current | = | I_1+I_2+I_3 |
| I_{Total} | = | 1amp+1amp+1amp |
| I_{Total} | = | 3amps |




