Logarithms - multiplication                                         

Mathematicians found an easier way.

Instead of multiplying numbers, they added powers (indices/exponents) and adding is a lot easier.

From our knowledge of indices.

`a^m\timesa^n = a^(m+n)`

or `10^2\times10^2 = 10^4`

`(10\times10)\times (10\times10) = (10\times10\times10\times10)`

Here is the example again

`69.31\times 57.43`

This is the same as `10^(1.8408)\times 10^(1.7591)` (see next page for explanation)

Add the indices 

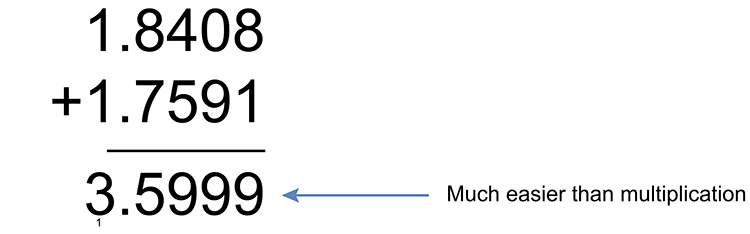
This equals `10^(3.5999)`

And `10^(3.5999) = 10^3\times 10^(0.5999)`

`= 1000\times 3.980`

`= 3980`

(see next sections for explanation)