Logarithms – divide large numbers traditionally 

Before the early 1970’s; before students had calculators:

It was incredibly difficult when dividing large numbers not to make a mistake.

For example `82,310 ÷ 162`

Answer:

`508.086` remainder `0.068`

Seriously try this divide and see if you make a mistake (for clarity we left out the subtraction workings out).

Logarithms Divide                                             

Mathematicians found an easier way.

Instead of dividing numbers

They subtracted powers (indices/exponents), and subtracting is a lot easier.

From our knowledge of indices:

`a^mdiva^n=a^m/a^n=a^(m-n)`

Or `10^3 ÷ 10^2 = 10^1`

`((10times 10 \times 10))/(10\ times 10) = (10)` 

Here is the example again:

`82310 ÷ 162`

Is the same as `10^4.9155 ÷ 10^2.2095`

Subtract the indices

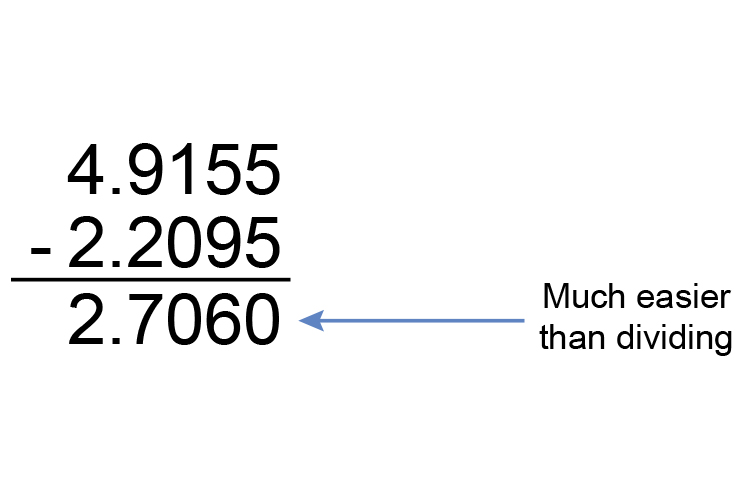
This equals `10^2.7060`

And `10^2.7060 = 10^2\times 10^0.7060`

`= 100\times 5.082`

`= 508.2`

(see below for explanation)

Explanation                                                                    

So how did we convert `82310 ÷ 162` into `10^4.9155 ÷ 10^2.2095`

We use log tables            (see reference log tables above)

First look up `82310`

Logs only work between `1` and `10`

And so `82310 = 10^4\times 8.231`

So we look up `8.231`

Here is part of the log table:

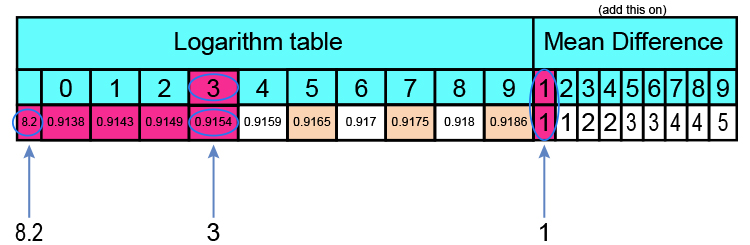
`0.9154 + 1` (to the last digit) = `0.9155`

Log table of `8.231 = 0.9155`

So `8.231 = 10^0.9155`

Therefore:  `82310 = 10^4\times 8.231`

    `= 10^4\times 10^0.9155`

    `= 10^4.9155` (adding indices)

Now look up `162`

Logs only work between `1` and `10`

And so `162 = 10^2times1.62`

So we look up `1.62`

Here is part of the log table:

(Reference log tables/reference anti-log tables above) 

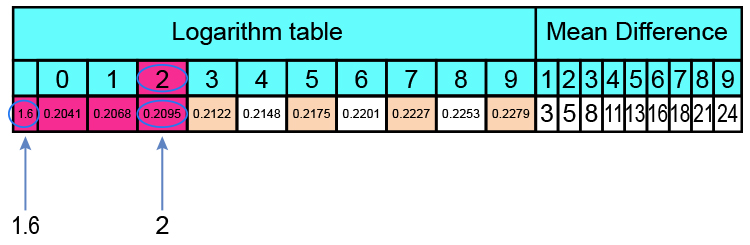
Log table of `1.62 = 0.2095` which is spot on

So `1.62 = 10^0.2095`

Therefore: `162 = 10^2times1.62`

     `= 10^2\times 10^0.2095`

     `= 10^2.2095` (adding indices)

So `82310 ÷ 162` is the same as `10^4.9155 ÷ 10^2.2095`

Subtract the indices

This equals `10^2.7060`

The antilog tables                                       

So how do we convert `10^2.7060` back to a normal number?

We use antilog tables                                    (see reference antilog tables above)

Antilog `10^2.7060`

Antilogs only work between `0` and `1`                                                     

So `10^2.7060 = 10^2\times 10^0.7060`

`10^2 = 10\times 10 = 100`

And we must look up `0.7060`

Looking up `10^0.7060`

Here is part of the antilog table:

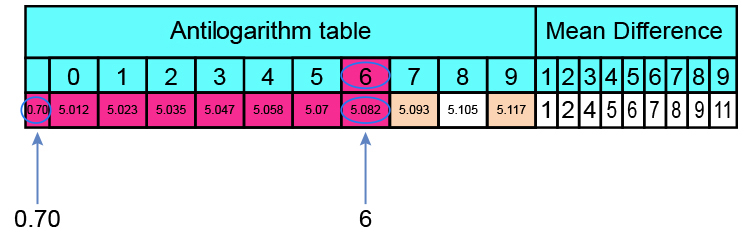
Antilog table of `0.7060 = 5.082`

So `10^0.7060 = 5.082`

Therefore `10^2.7060 = 10^2\times 10^0.7060`

      `= 100times5.082`

    `= 508.2`