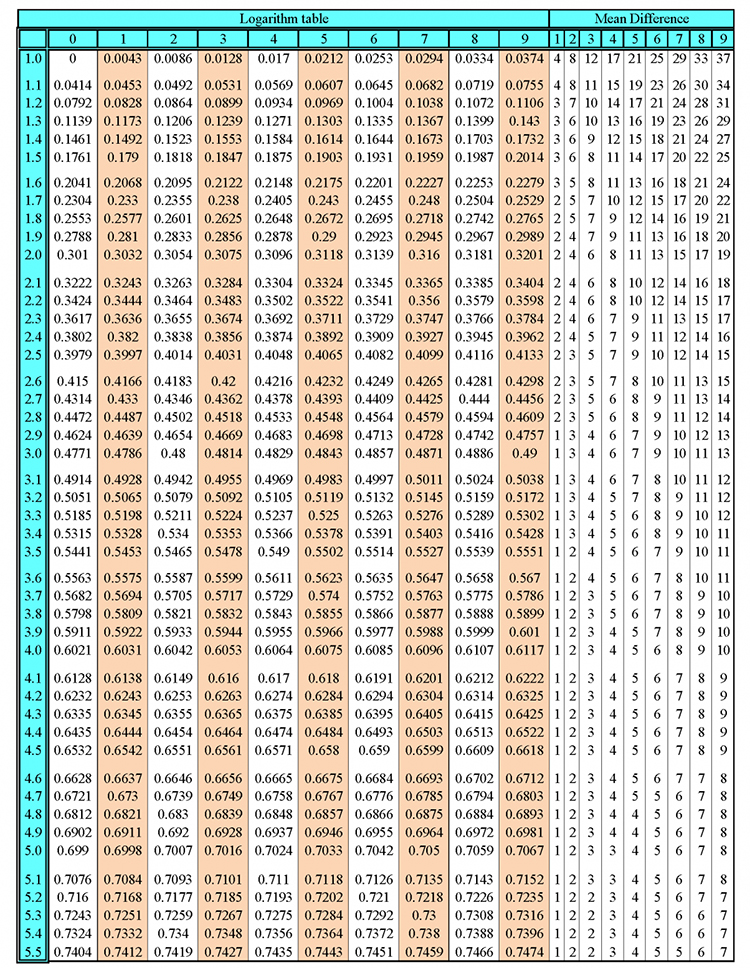
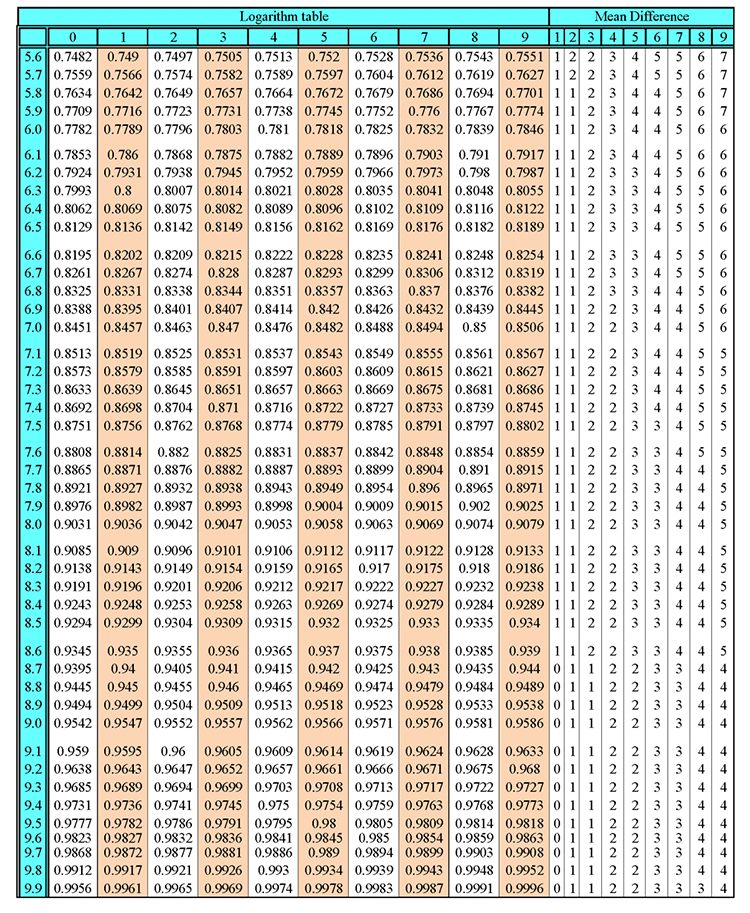
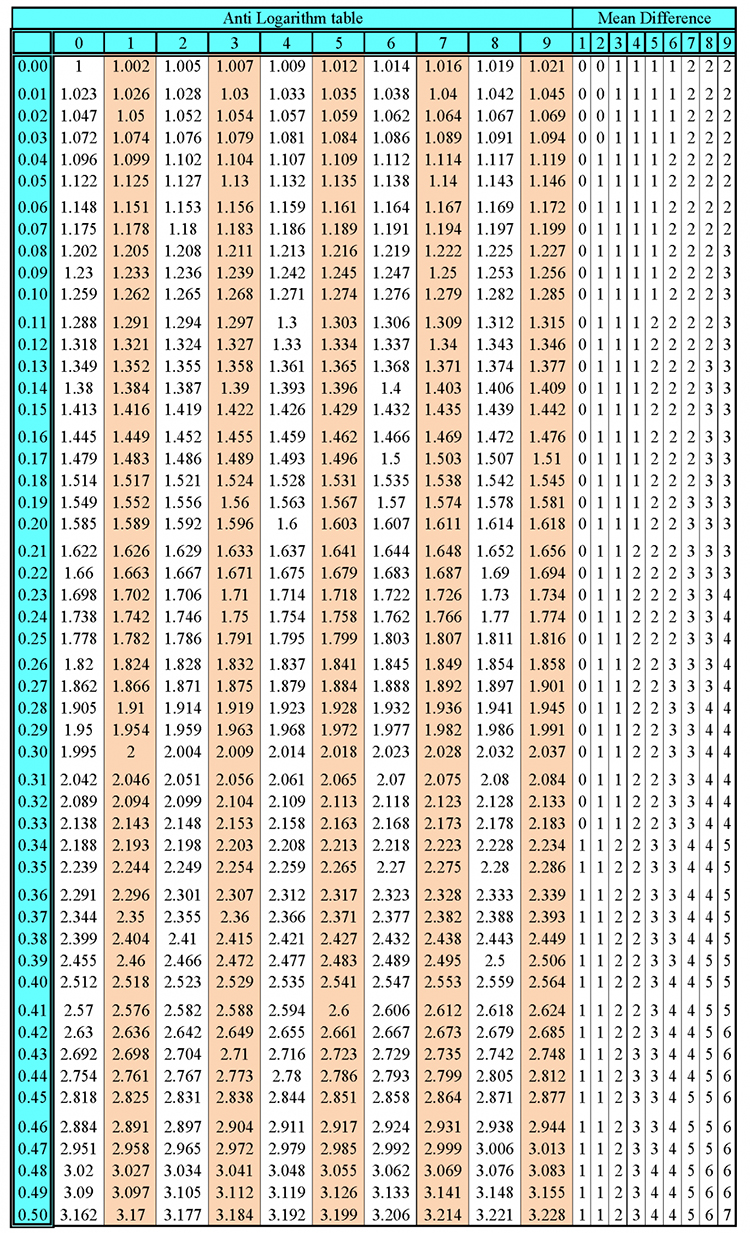
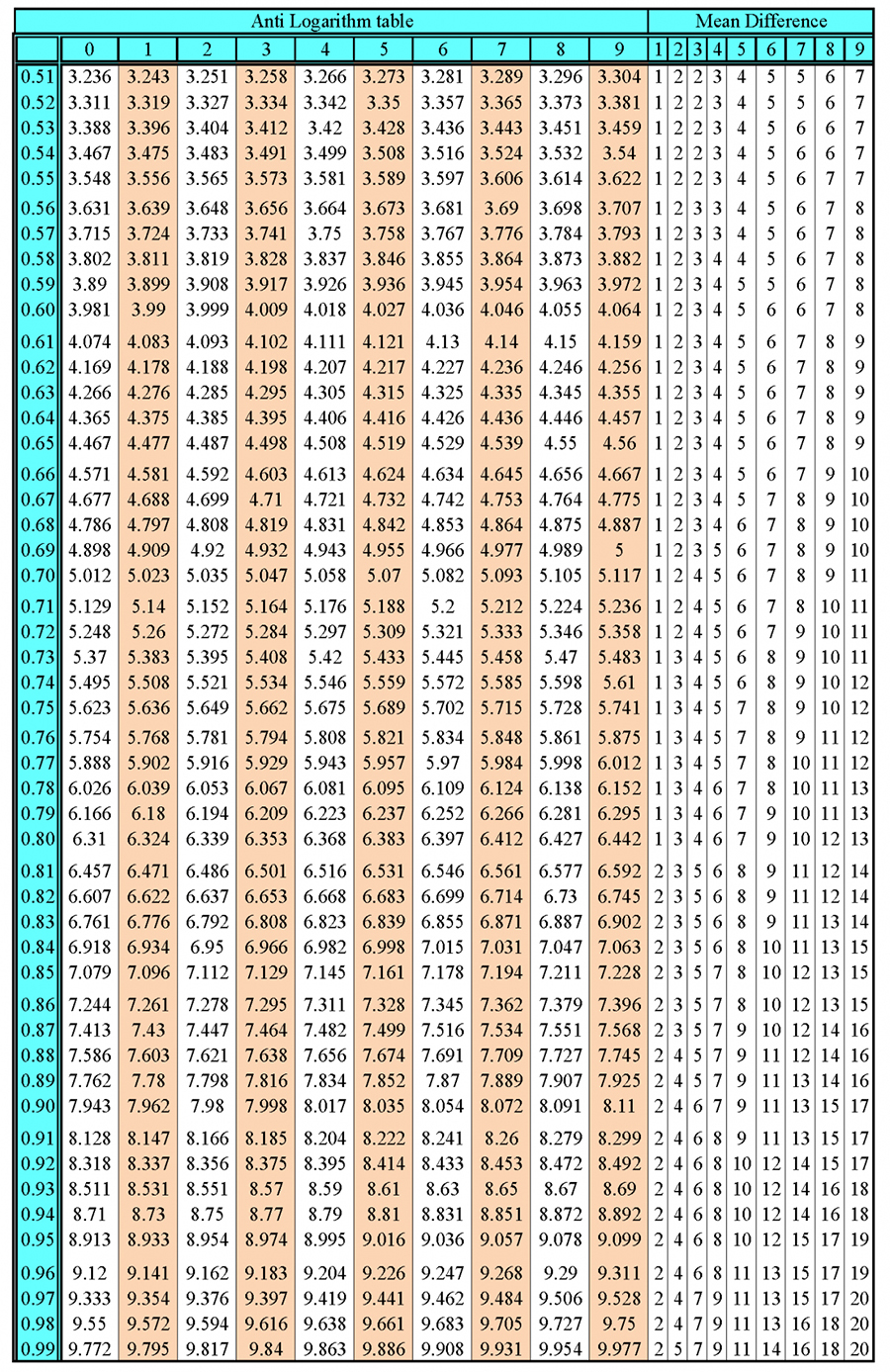
Number Bases and binary
Number bases – Are a table built on multiples of the chosen base number. Start with the number 1 and multiply 1 by the chosen base number and keep multiplying by the base. Work right to left not left to right.

The bass (base) must be multiplied to hear it. You start with one bass (one base) guitar.
Example 1
Write the sequence of headings for base 10.

Start by writing the number 1 down on the right hand side

Multiply one by 10 to get the next heading number
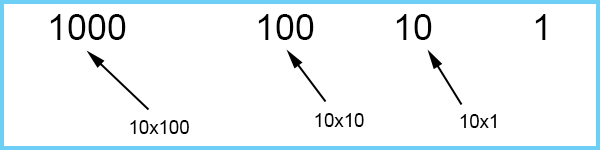
And keep multiplying by 10.
The sequence for headings of base 10 is:

Example 2
Base 2 (also known as the binary system) and is only made up of two numbers 0 (zero) and 1 (one). This system is used to write instructions for computer processing and is often called binary code.

Start by writing the number 1 down on the right hand side

Multiply one by 2 to get the next heading number.
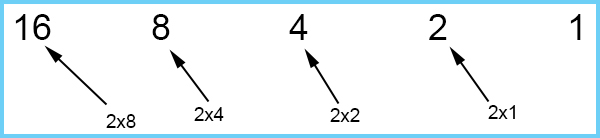
And keep multiplying by 2.
The sequence for headings of base 2 is:
![]()
Example 3
Base 8

Start by writing the number 1 down on the right hand side

Multiply one by 8 to get the next heading number.
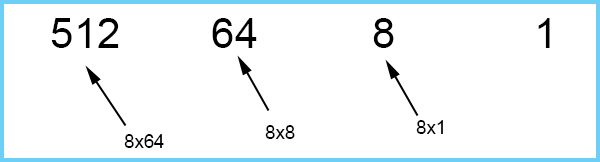
And keep multiplying by 8.
The sequence for headings of base 8 is:

Example 4
Base 5

Start by writing the number 1 down on the right hand side

Multiply one by 5 to get the next heading number.
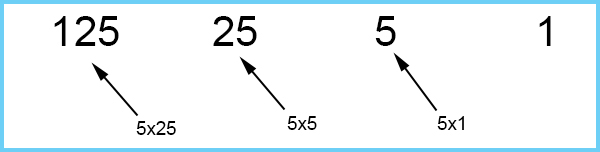
And keep multiplying by 5.
The sequence for headings of base 5 is:

Writing numbers in different bases
Example
Write 18 in each base 10, 2, 8 and 5
Base 10
|
1000 |
100 |
10 |
1 |
|
1 |
8 |
This means 1 ten and 8 ones = 18
Answer: 18 in base 10 is 18
Base 2
|
16 |
8 |
4 |
2 |
1 |
|
1 |
0 |
0 |
1 |
0 |
This means 1 sixteen, no 8’s, no 4’s, 1 two and no 1’s = 18
Answer: 18 in base 2 is 10010
Base 8
|
512 |
64 |
8 |
1 |
|
2 |
2 |
This means 2 eights and 2 ones = 18
Answer: 18 in base 8 = 22
Base 5
|
125 |
25 |
5 |
1 |
|
3 |
3 |
This means 3 fives and 3 number ones = 18
Answer: 18 in base 5 = 33