Creating a direct current (DC)

We can create an alternating electric current by turning a handle to rotate a coil of wire between two magnets, inducing a current in the wire, as below:

NOTE: that one half of the coil between the magnets is coloured black, and the other half blue.

For the first half of a rotation, the left (blue) side of the coil swings past the north pole of the left magnet, but for the second half of the rotation, it swings past the south pole of the right magnet (see below). The same thing happens, but in reverse, on the black side of the coil.

As a result, in the absence of a commutator, the coil would generate a current in one direction for the first half of the rotation, and in the opposite direction for the second half of the rotation.

A current like this – which switches continually between positive and negative – is called an alternating current (AC) (see previous page – CREATING ALTERNATING CURRENT). But what we want is direct current, which goes continually in the same direction. The commutator is the key to achieving this.

The commutator consists of two half-cylinders of smooth conducting material that are separated by small gaps. Each half-cylinder is connected to one end of the coil of wire, and the commutator rotates with the coil. Two stationary brushes, made of carbon, press against the spinning commutator. These brushes act as the terminals (outputs) of the direct current (DC) generator.

As the commutator turns, contact with the brushes alternates between the two halves of the commutator switching the polarity. The switch made by the commutator happens the instant the voltage in the coil would normally reverse polarity.

This ensures that the current produced no longer fluctuates between positive and negative, but continues in the same direction (given that the handle continues to be turned in the same direction.) This is direct current.

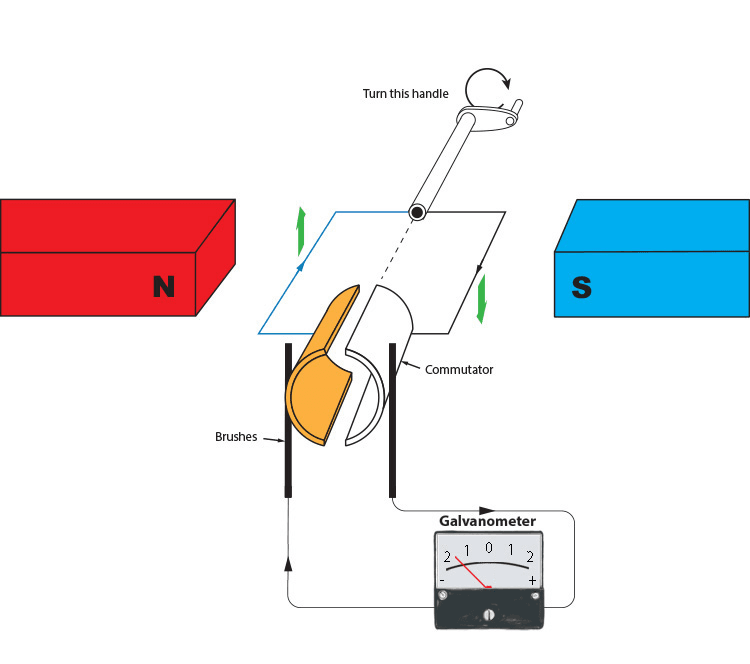
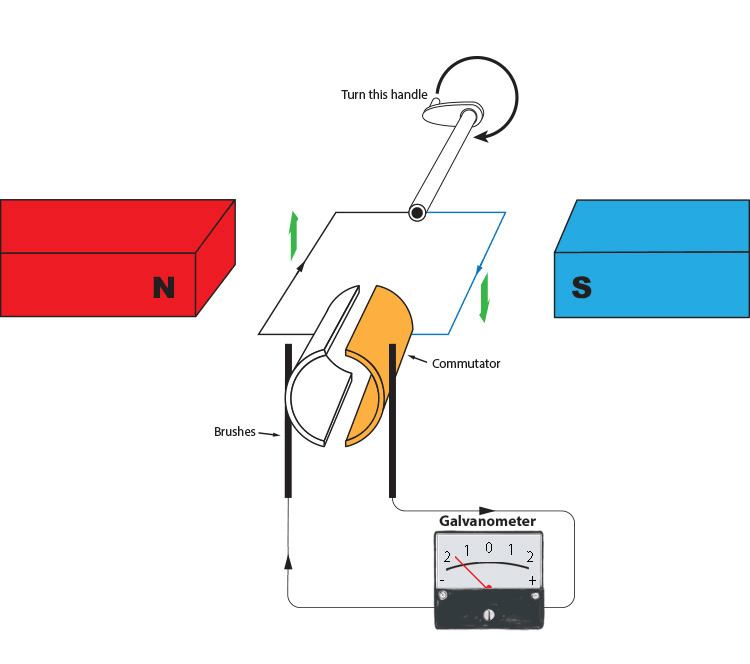
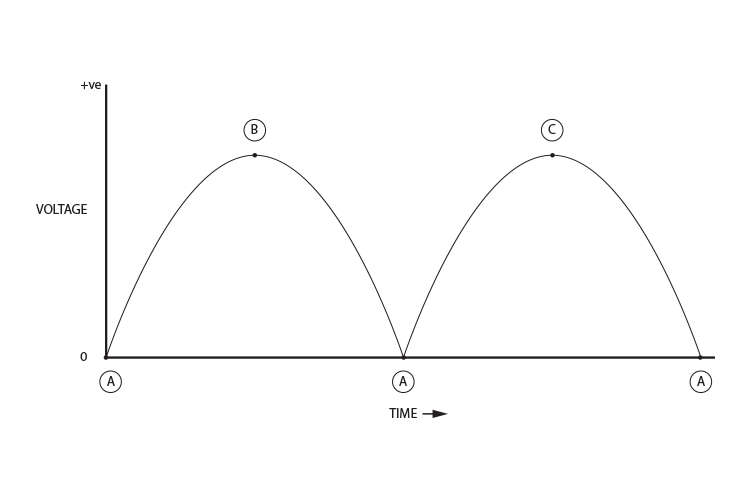
The galvanometer will show a movement from a peak back to zero and back up to the peak. But never does it reverse direction.

If you were to plot the voltage change through time for one complete 360° revolution of the handle, you would find the following:

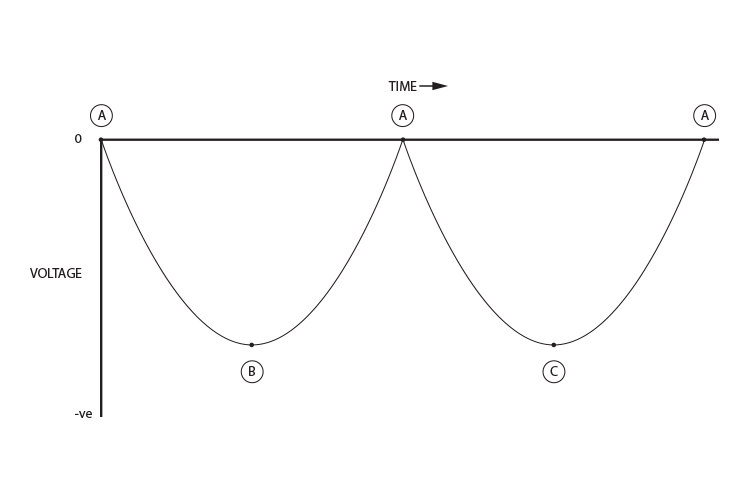
Or, if you turned the handle the opposite way: