Principal focal length of an eye and power

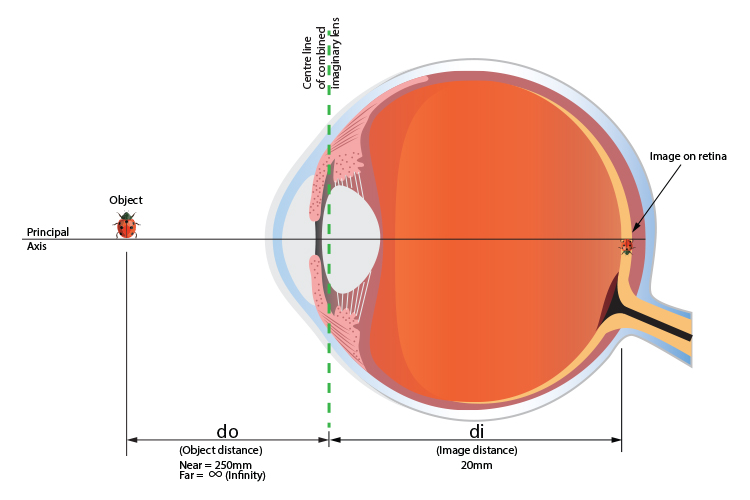
Using a simplified version of an eye, it is easy for us to work out the principal focal point of the eye.

What is different about the eye is that as the object moves the retina cannot. The image must always appear clearly on the retina as the principal focal point changes. This is carried out by the eye changing the thickness of the lens (unlike a camera) according to whether there is a near or far object. 

The nearest a human eye can focus an object is 250mm from the front of the lens. The furthest is infinity.

Let's find the principal focal length for a human eye at the near point (250mm away) and then do the same for a far point.

We know the lens equation (see Mammoth Memory convex lens and concave lens)

`1/f=1/(d\o)+1/(d\i)`

`f=` Principal focal length

`d\o=` Object distance from centre of convex lens

`d\i=` Image distance from centre of convex lens

The principal focal point – nearest point

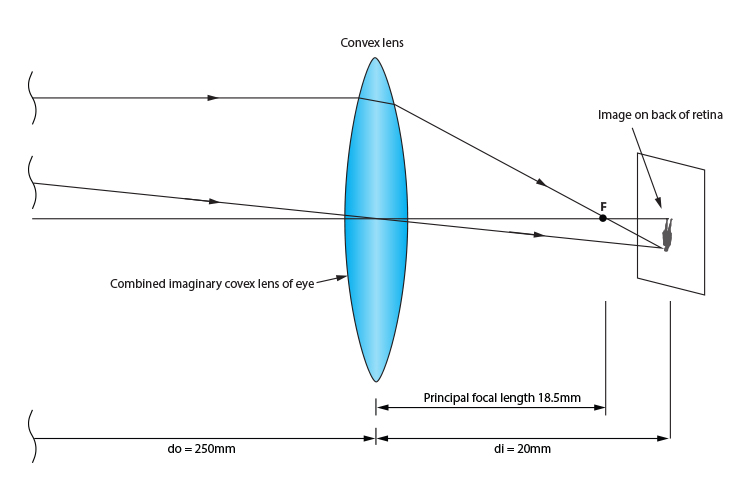
For an object at 250mm from the eye the principal focal length would be:

`1/f=1/(d\o)+1/(d\i)`

`1/f=1/250+1/20`

`1/f=0.004+0.05`

`1/f=0.054`

`f=18.5mm`

This would translate as:

The principal focal point – furthest point

For an object a very long way away we call this infinity

`1/f=1/(d\o)+1/(d\i)`

`1/f=1/(infty)+1/20`

As one divided by infinity is zero the formula becomes

`1/f=0+0.05`

`1/f=0.05`

`f=20mm`

At infinity an image is so small that it would probably register as a blur of light like a star in the sky.

If the position of the object is between infinity and the near point of the eye then the eye lens adjusts its principal focal length in between 18.5mm and 20mm. This is a difference of 1.5mm. This 1.5mm difference is called adjustment or lens adjustment.

Just as we have now worked out the principal focal length changes, we can also find the change in power of the lens from near to infinite distances.

Power – near point

For an object at 250mm from the eye and with the principal focal length being 18.5mm, the power of the lens combination would be.

`P=1/f`

`P=1/0.0185`

`P=54D`

For an explanation of `D` see Mammoth Memory magnification.

Power – furthest point

For an object a very long way away, we now know that the principal focal length would be 20mm and therefore the power of the lens combination would be.

`P=1/f`

`P=1/0.02=50D`

Conclusion

The power of the eye ranges from `50D` for distance and `54D` for close objects. This is an 8% increase in power or an 8% ability to accomodate.