Multiplying Brackets
Method 1 - The arrows method
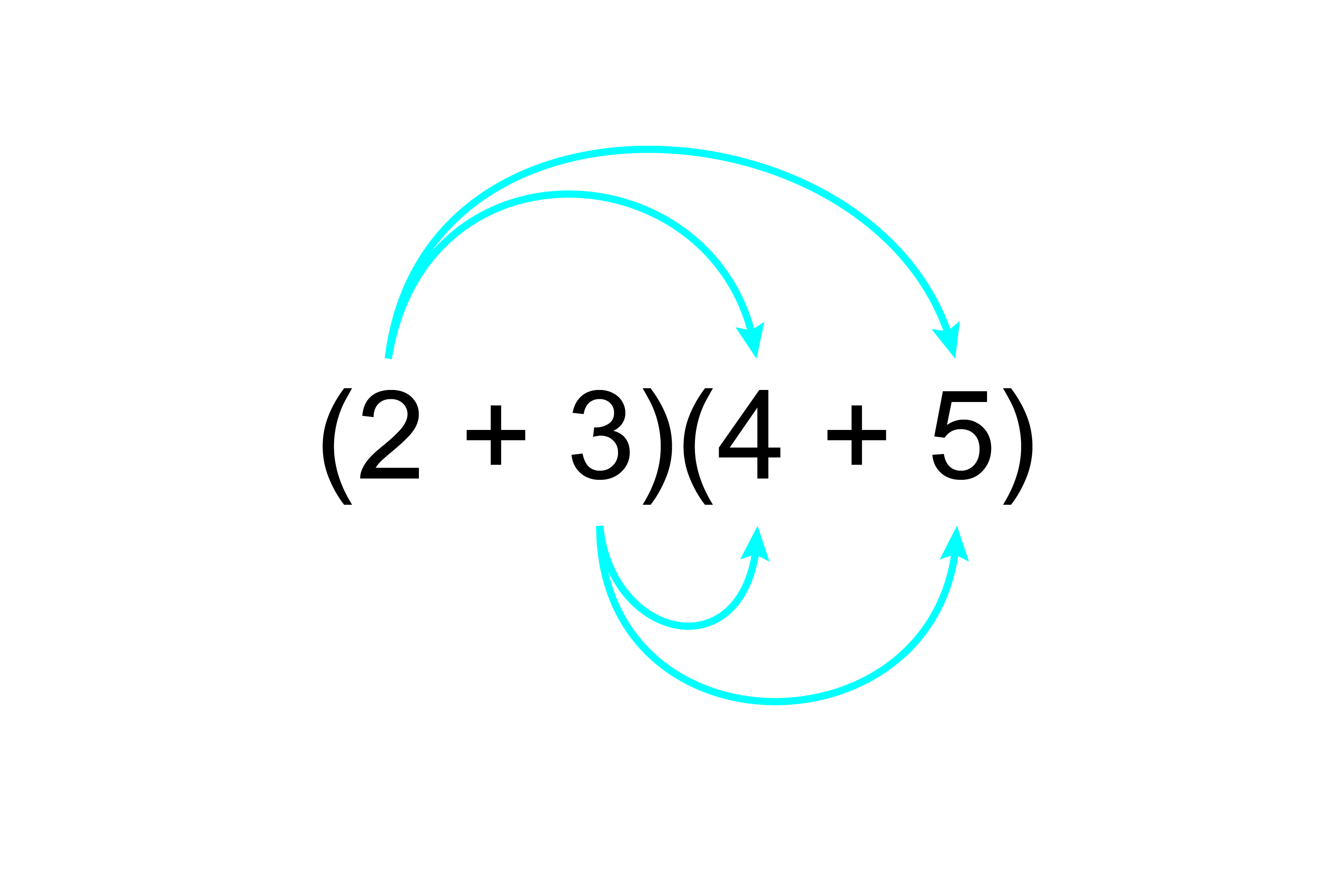
`2times4+2xx5+3xx4+3xx5`
`=8+10+12+15`
`=45`
Method 2 – The woman with the big nose
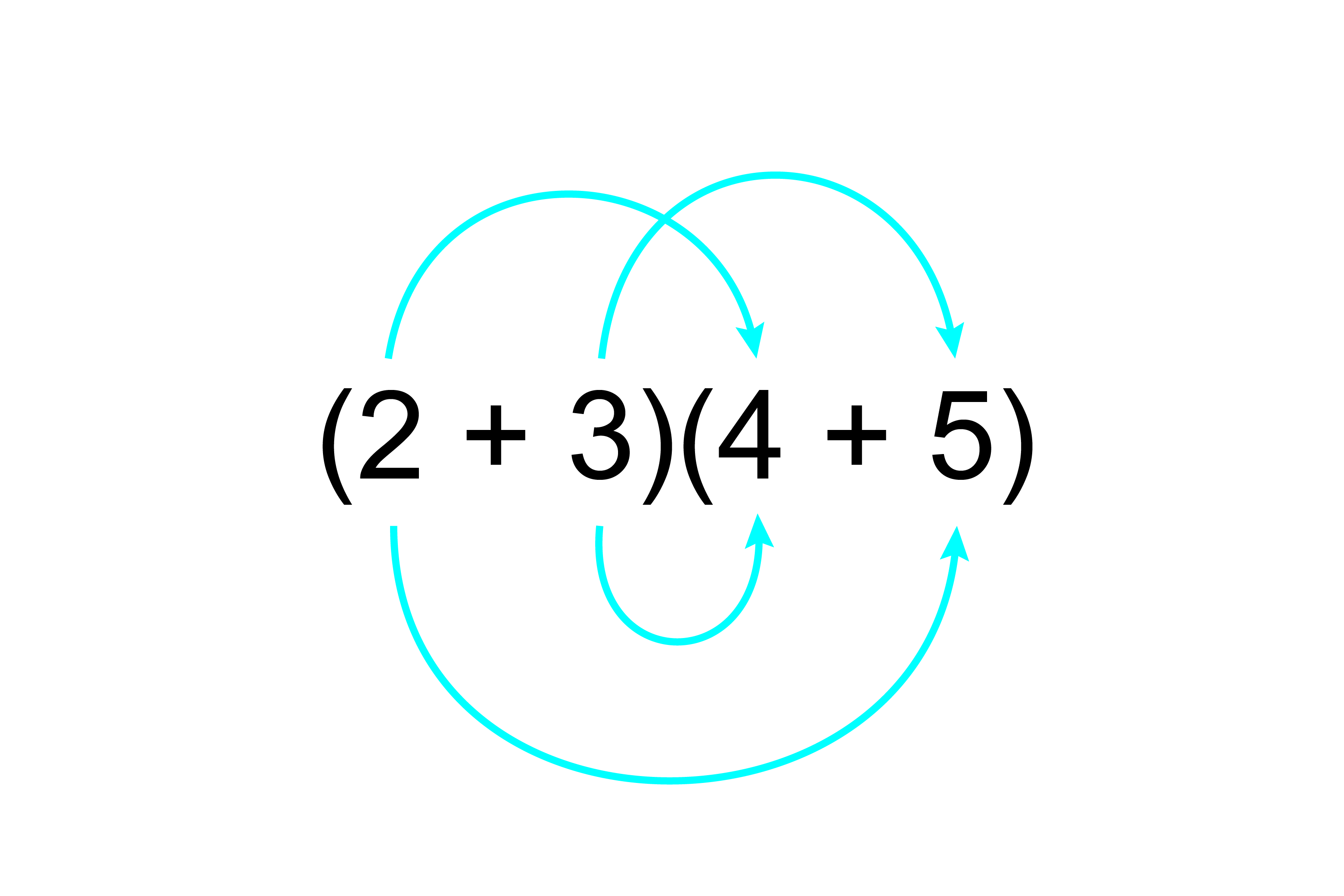
The woman with the big nose.
`2times4+2xx5+3xx4+3xx5`
`=8+10+12+15`
`=45`
Method 3 – The box method
`(2+3)(4+5)`
Stage 1
|
|
4 |
5 |
|
2 |
|
|
|
3 |
|
|
Now multiply the rows with the columns.
Stage 2
|
|
4 |
5 |
|
2 |
8 |
10 |
|
3 |
12 |
15 |
Now take the numbers out of the boxes.
`=8+10+12+15`
`=45`
Method 4 - A visual way to remember multiplying out brackets
`(a+b)^2=a^2+2ab+b^2`
Which can be visualised as follows:
Then
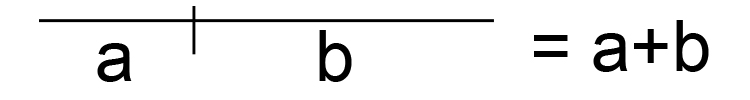
But we want `a+b` squared
So lets make a square
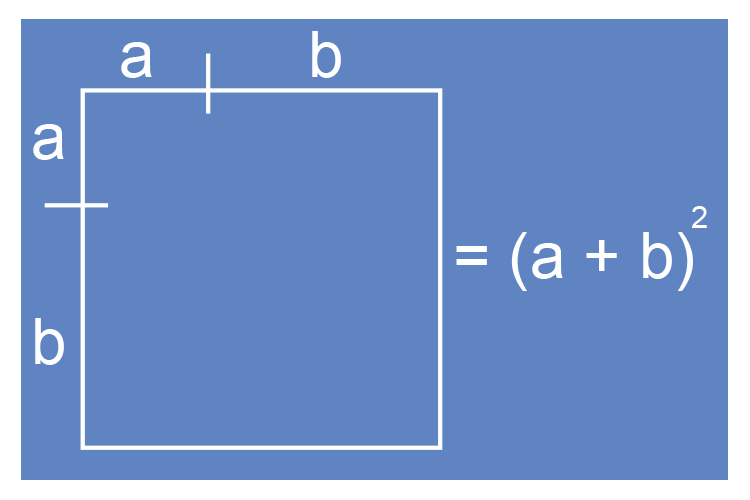
Now fill in the box
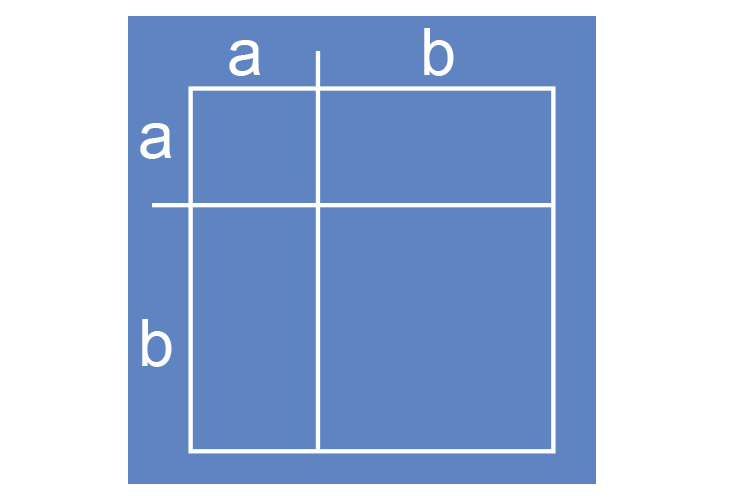
The area of each square is:
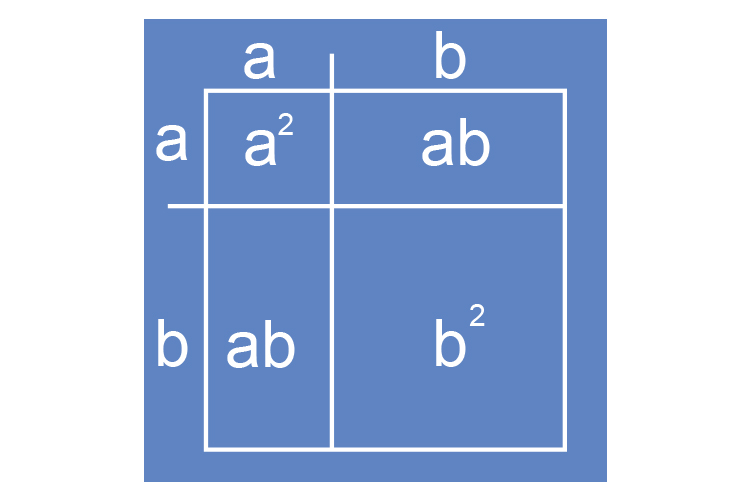
So the area of this square is `a^2+ab+ab+b^2`
Which equals
`a^2+2ab+b^2`
So that's why
`(a+b)^2=a^2+2ab+b^2`
Examples
All four methods work but we will use method 1
1. Multiply out `(a+b)(c+d)`
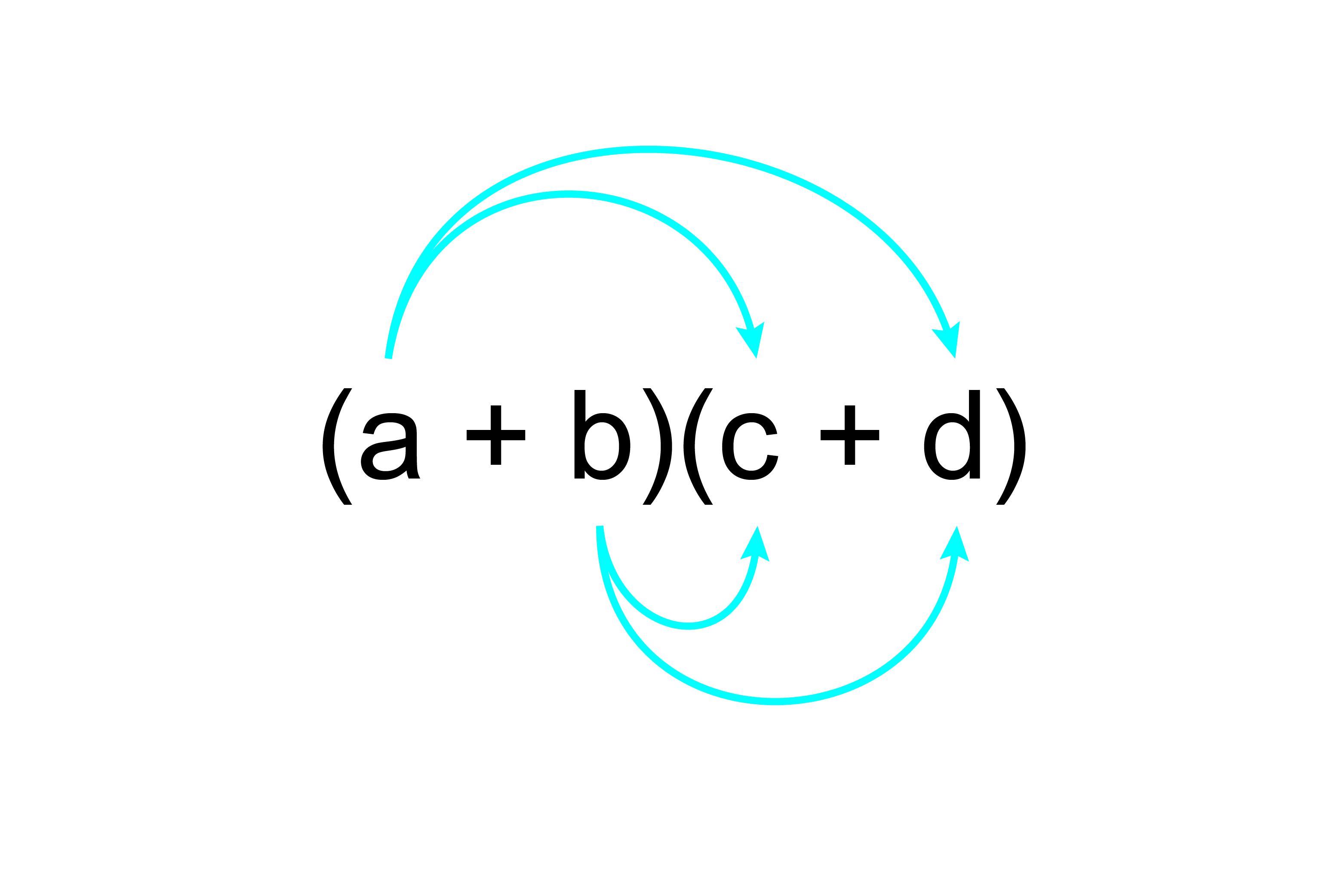
`ac+ad+bc+bd`
Answer: `(a+b)(c+d)=ac+ad+bc+bd`
2. Multiply out `(5x+4y)(3x-4y)`
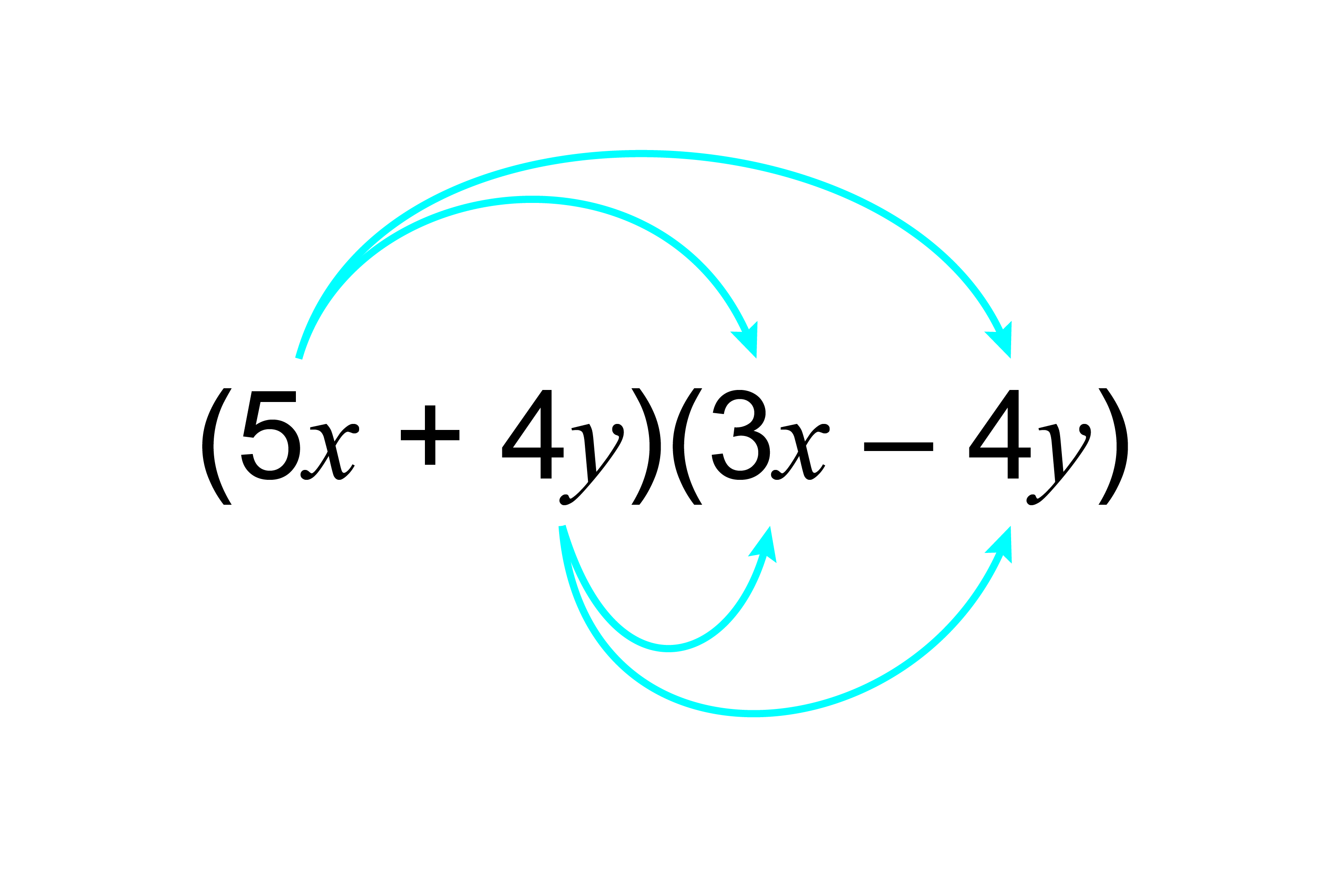
`5xtimes3x+5x(-4y)+4ytimes3x+4y(-4y)`
`15x-20xy+12xy-16y^2`
`15x-8xy-16y^2`
Answer: `(5x+4y)(3x-4y)=15x-8xy-16y^2`
3. Multiply out `(x+8)^2`
This is the same as `(x+8)(x+8)`
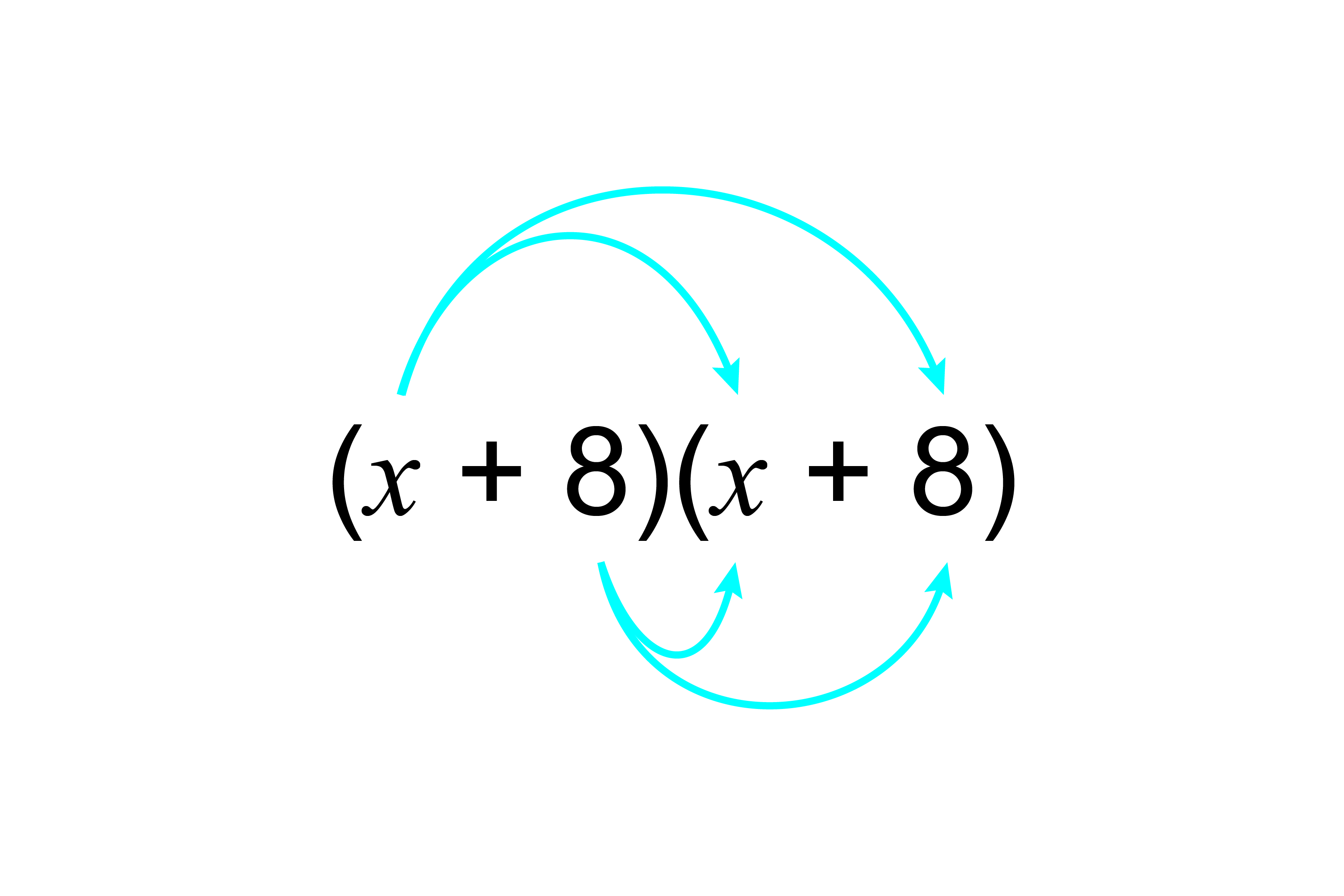
`x^2+8x+8x+8times8`
`x^2+16x+64`
Answer: `(x+8)^2=x^2+16x+64`
4. Multiply out `3(4x-7)`
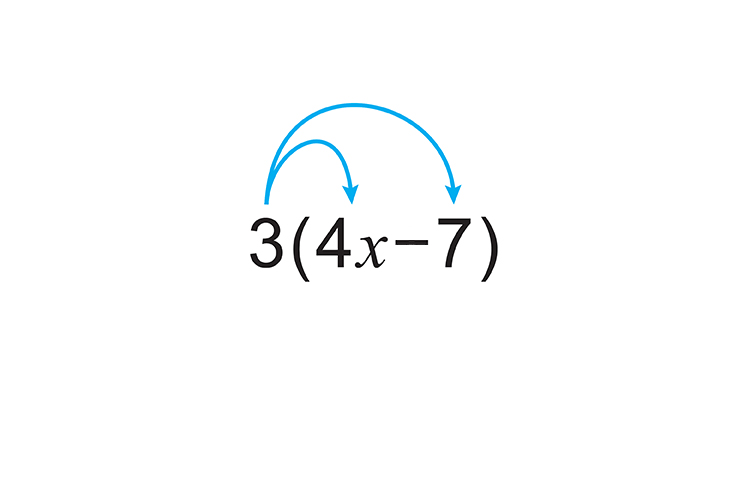
`3times4x-3times7`
`12x-21`
Answer: `3(4x-7)=12x-21`
5. Multiply out `3xy(2x+y^2)`
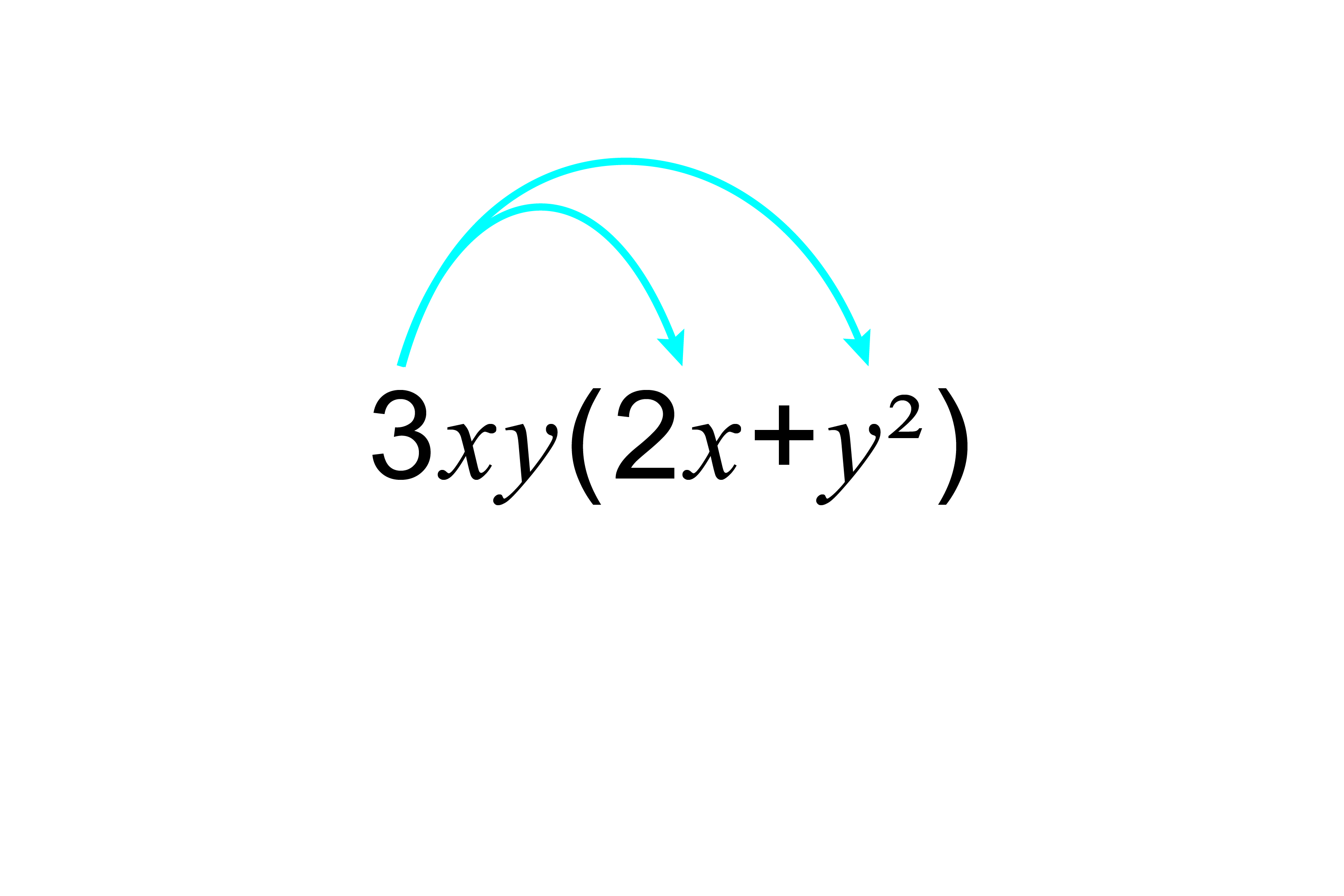
`3xytimes2x+3xytimesy^2`
`3timesxtimesytimes2timesx+3timesxtimesytimesytimesy`
`6x^2y+3xy^3`
Answer: `3xy(2x+y^2)=6x^2y+3xy^3`




