Two part ratios

When you hear the word ratio you must try to remember the words "to every"

If something is `1` to `5` ratio you must read this as `1` to every `5`

A ratio shows how two numbers compare.

`x` to every `y`

To help you remember ratio is "to every" see below

A ratio is 2 numbers to say how many numbers in another

Raise a toe (ratio) to every (to every) one.

Ratio `=` to every

There are several ways mathematicians express ratios

`5:1` ratio `=5` to every `1`

`5/1` ratio `=5` to every `1`

`5` to `1` ratio `=5` to every `1`

Example 1

A train has been built at a ratio of `1:12.5`. If the model train is `35cm` tall how tall is the real thing?

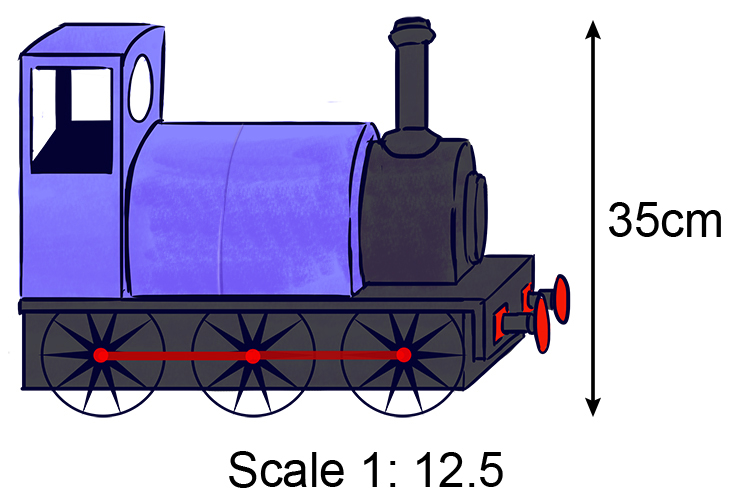
if a scale is 1:12.5 then for every 1 there is 12.5

The ratio is `1` to every `12.5`

so `1cm` to every `12.5cm`

If `1=12.5`

then `35=x`

(treat this like all calculations in our percentages section)

Put a divide sign between them

`1/35=12.5/x`

rearranging

`x=(12.5times35)/1`

`x=437.5cm`

Answer:

The real train is `437.5cm` tall.

Example 2

To make biscuits you need `350\ grams` of wheat. This makes 22 biscuits. How many grams of wheat do you need to make 30 biscuits?

So the ratio is `22` biscuits to every `350\ grams` wheat.

`22=350`

Work out `1` biscuit

`1=x`

(treat this like all the calculations in our percentages section).

Put a divide sign between them

`22/1=350/x`

rearrange

`x=(350times1)/22`

`x=15.9\ grams` of wheat.

so the ratio is

`1` biscuit to every `15.9\ grams` of wheat

Now we can work out 30 biscuits.

`1=15.9`

`30=x`

(treat this like all the calculations in our percentages section).

Put a divide sign between them.

`1/30=15.9/x`

rearranging

`x=(15.9times30)/1`

`x=477\ grams`

Answer:

`477\ grams` make `30` biscuits.