Intercept theorem examples

Example 1

A lady wants to get onto a flat roof and needs to work out what size ladder she needs. 1.8 metres up, there is a bracket sticking out of the wall. The bracket casts a shadow 3 metres away from the base. The flat roof casts a shadow 8 metres from the base. How high is the roof?

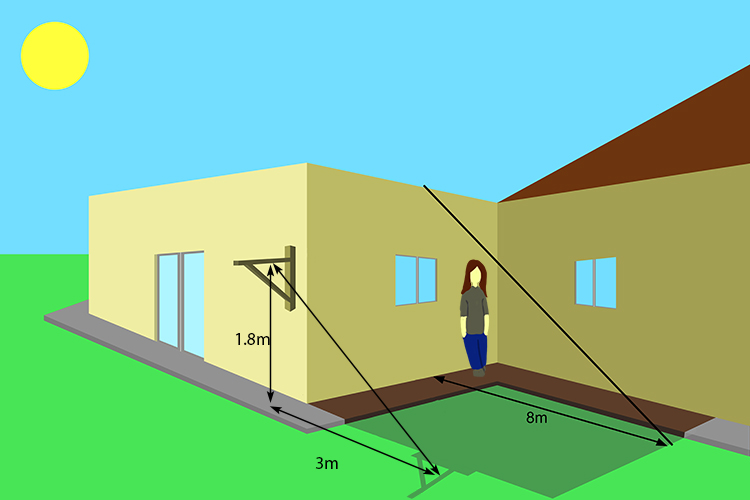
Example of an exam question of the intercept theorem

Redraw this diagram as:

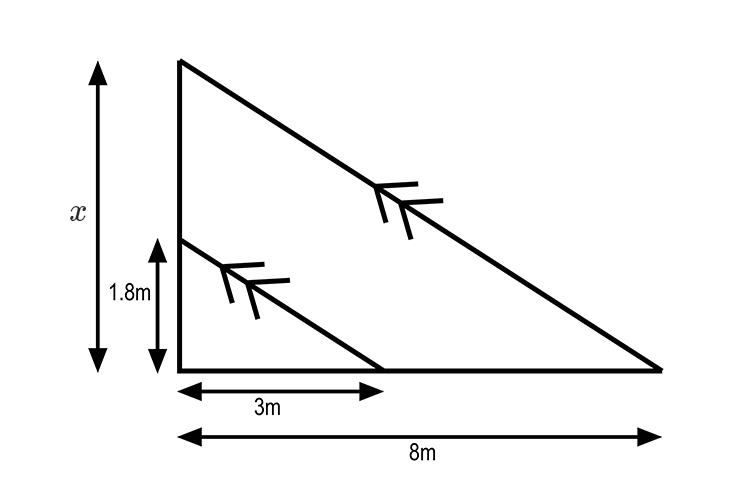
Redraw the triangle of the shadow in 2D then add the extra parallel line to match the long length of the triangle

Remember - Thales' intercept theorem states that the segments created by parallel lines are proportional.

Therefore `3/8=1.8/x`

Rearrange `x` to be the subject of the formula.

`x=(1.8times8)/3`

`x=4.8`

Answer: The height of the flat roof is 4.8m.

Example 2

In the following diagram what is the value of `x`?

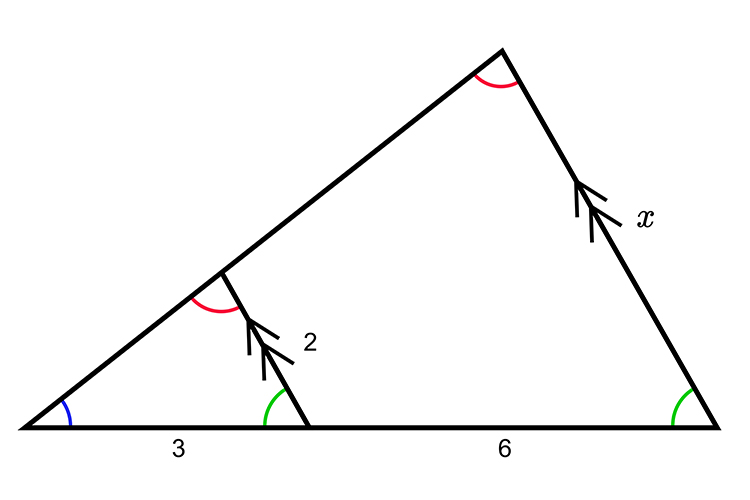
Using the intercept theorem work out the length of x

Remember that Thales' intercept theorem states that the segments created by parallel lines are proportional.

Therefore `3:(3+6)` is proportional to `2:x`

`3/(3+6)=2/x`

`3/9=2/x`

Rearrange to make `x` the subject of the formula:

`x=(2times9)/3=18/3`

`x=6`

NOTE:

`3:6` is not proportional to `2:x` because 6 is not the full length of the side of the triangle.

Example 3

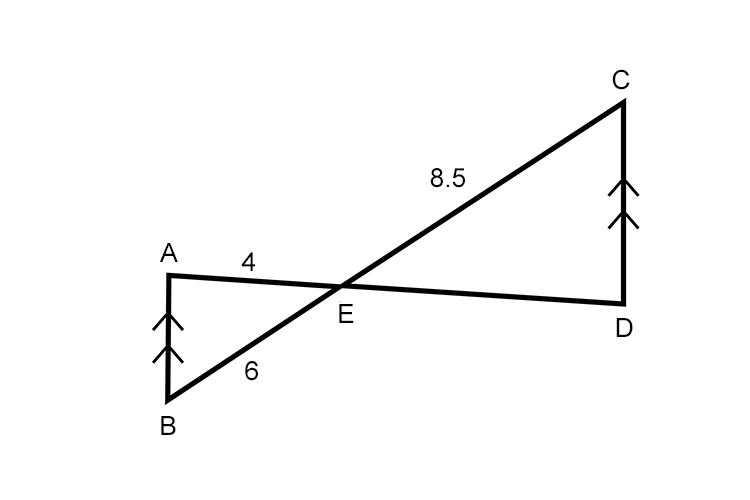
Using the parallel lines of this shape work out the length of side ED

In the above diagram, AB is parallel to DC. How long is ED?

Answer:

If AB and CD are parallel then these two triangles are similar and so the diagram above can be
re-drawn as:

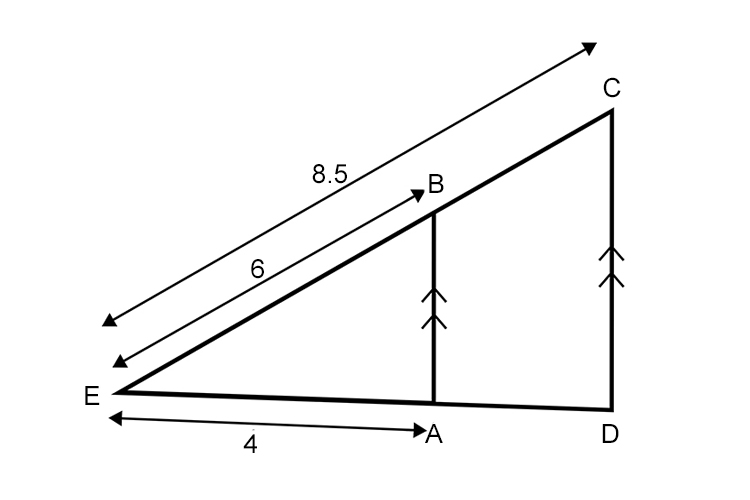
Answer to example 3 explained, length ED equals 5.66

Triangle ABE has been spun through 180° with point E as the pivot point.

Now the question "how long is ED?" is easy.

Using Thales' intercept theorem (with parallel lines) the triangle sides would be proportional i.e.

`8.5/6=(ED)/4`

Rearrange the formula so that ED is the subject of the formula.

`ED=(8.5times4)/6`

Answer: ED = 5.67

Example 4

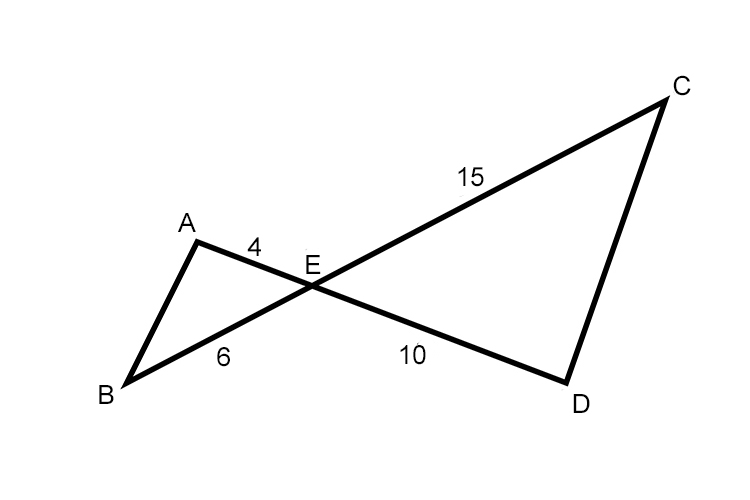
Are lines AB and CD parallel?

If they are parallel then these two triangles are similar and so can be re-arranged as:

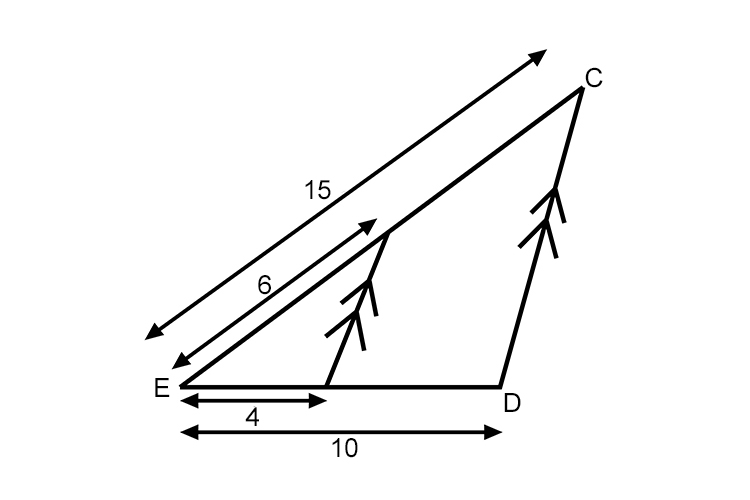
Take just the parallel lines and complete a triangle using the longest length as the down stroke

And using Thales' intercept theorem (with parallel lines) full length triangle sides would be proportional i.e.

`4/10` Would be proportional to `6/15`

`2/5=0.4` `3/7.5=0.4`

As they are the same answer then the lines AB and CD are parallel

Example 5

If the lines CD and BE are parallel which of the following equations are correct?

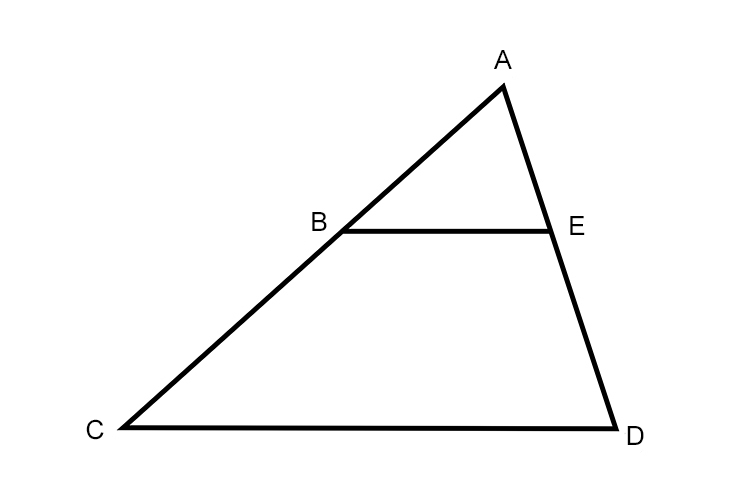
Using the triangle which of the equations are correct to match the shape

`(AC)/(CD)=(BE)/(CD)=(AB)/(AE)` or `(AB)/(AC)=(AE)/(AD)=(BE)/(CD)` or `(CB)/(CA)=(DE)/(DA)=(CD)/(BE)` or `(CB)/(CA)=(DE)/(DA)=(BE)/(CD)`

To check this out remember Thales' intercept theorem that if two intersecting lines are intercepted by parallel lines, then the segments created are proportional.

Example 6

In the following diagram how long is AB?

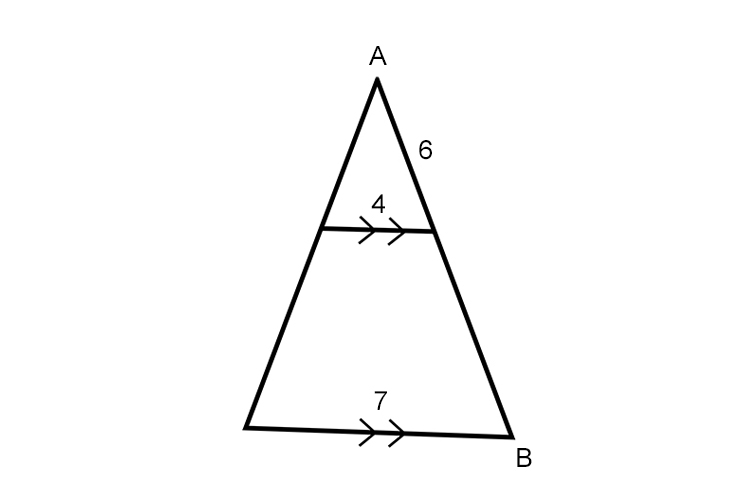
Using the parallel lines work out the length of AB

Two sides are parallel.

Therefore `6/(AB)=4/7`

`AB=(6times7)/4=42/4=21/2=10.5`

Answer: AB is 10.5

Example 7

Are the lines AB and CD parallel?

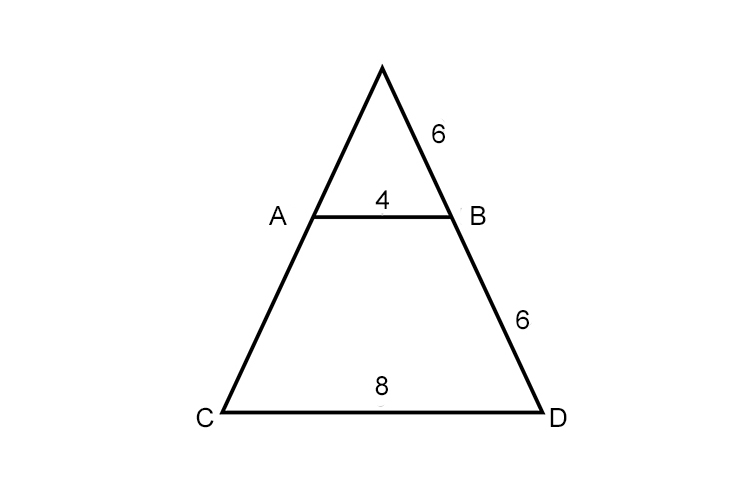
Questions like this catch people out, you have to show your workings to explain why the lines are parallel. Only then can you get the mark

If they are then `6/12=4/8`

`1/2=1/2` So yes AB and CD are parallel.