Triangles

What Thales realised was that he had created similar triangles with parallel lines.

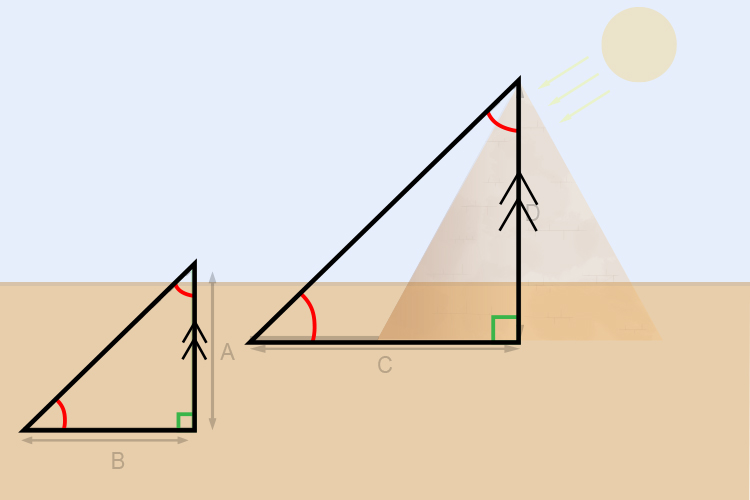
Thales found that the triangles he had created with the pyramid and poles had matching parallel lines, this meant he could measure the proportional values for each length

As long as the two sides were parallel he could work out proportional values for the lengths of the lines.

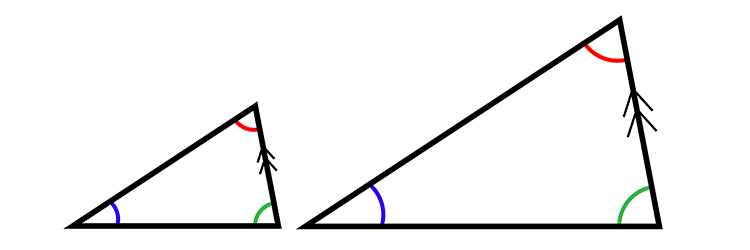
As long as the lines of both triangles are parallel the calculation can take place

Similar triangles with two parallel lines.

So Thales then used this information to measure the width of a river.

With this information he found he could measure lots of things including the width of a river

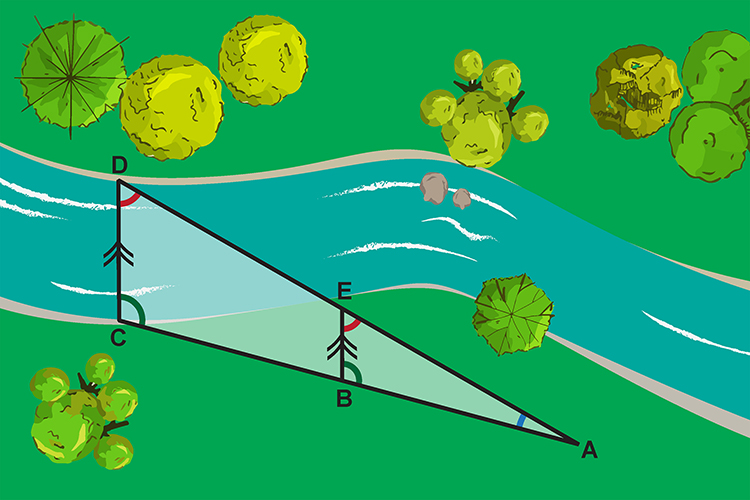
As long as CD and BE are parallel he found the width of this river because of similar triangles with parallel lines.

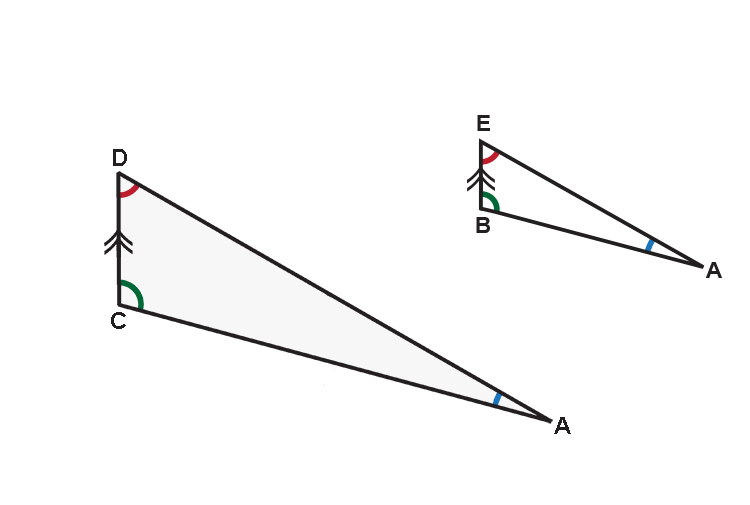
Thales then found the ratio CD over AC is BE over AB by measuring A to C and A to B and B to E he could determine CD such as distance across water

Similar triangles with parallel lines.

And therefore he found the ratio

$(CD)/(AC)$ is identical to $(BE)/(AB)$

Thales could measure A to C and A to B and B to E and so he could determine C to D i.e. distance across the water.

Thales extended this to working out how far away ships were directly from his line of vision.

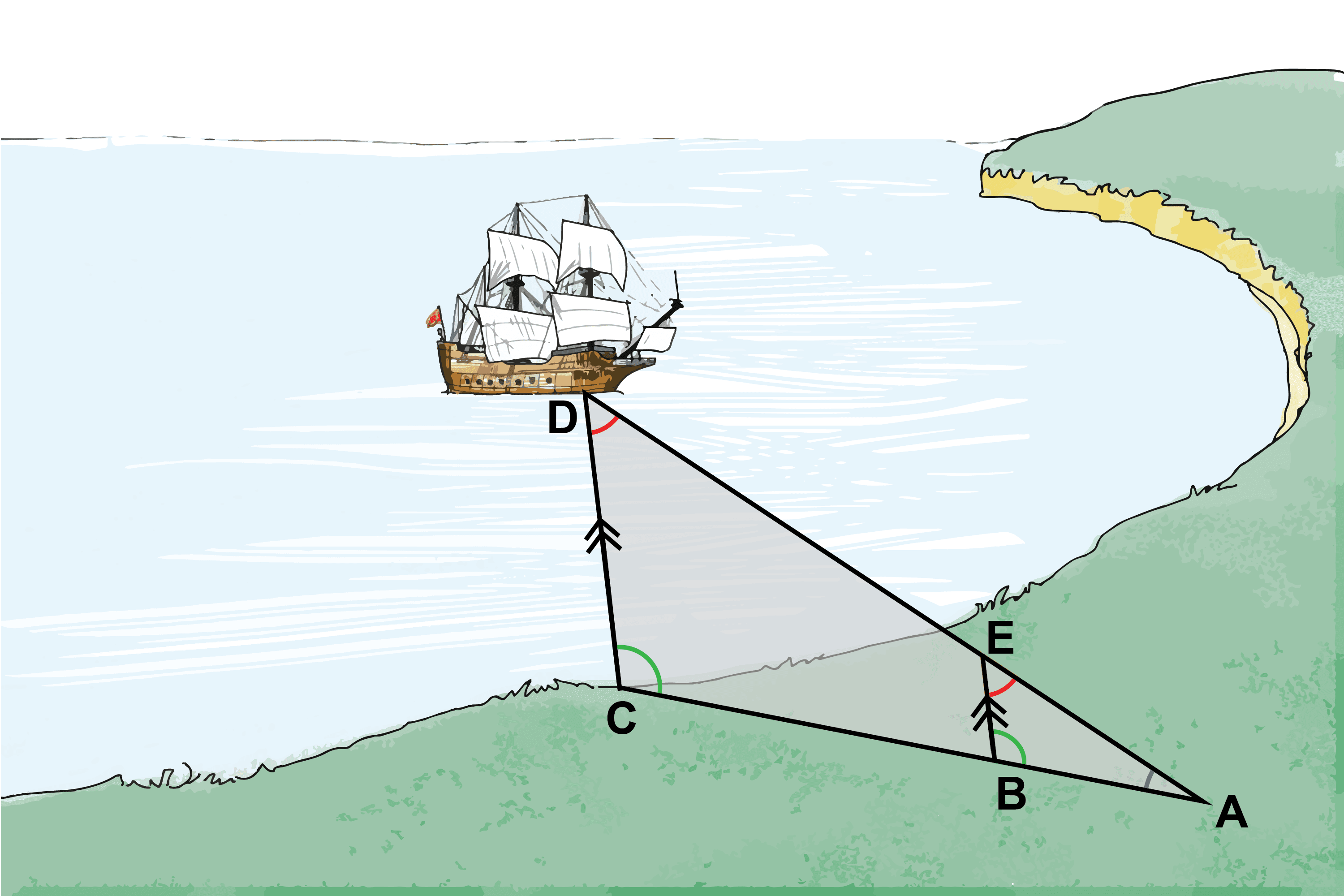
He could now measure the distance of a vessel from the coast to determine weapon firing distances

Even if the ship was miles out he could determine how far away the ship was. His method could even be used for working out firing distances.

He found

$(A\ text(to)\ B)/(A\ text(to)\ C)=(A\ text(to)\ E)/(A\ text(to)\ D)$

He then realised that as long as the triangles were similar EVERYTHING IS PROPORTIONAL to each other as ratios.

Even $(A\ text(to)\ B)/(A\ text(to)\ C)=(B\ text(to)\E)/(C\ text(to)\D)$

Or $(A\ text(to)\ E)/(A\ text(to)\ D)=(B\ text(to)\E)/(C\ text(to)\D)$

Conclusion

Thales' Intercept theorem – If two intersecting lines are intercepted by a pair of parallel lines, then the segments created are proportional.

So, in this example:

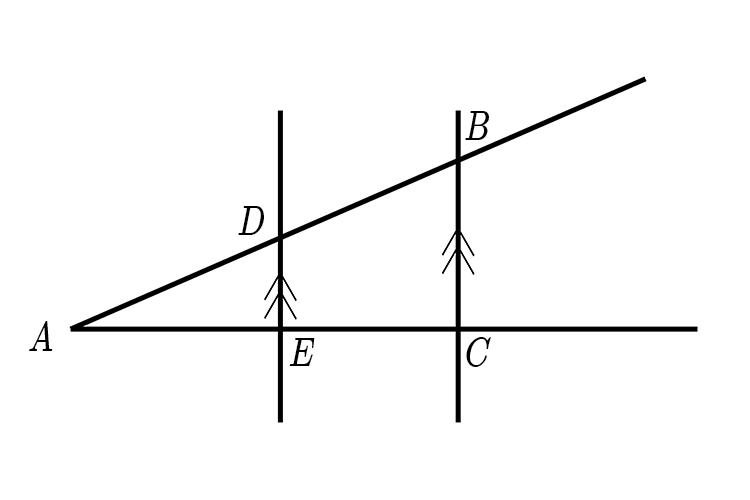
Thales Intercept theorem If two intersecting lines are intercepted by a pair of parallels

$(AE)/(AC)=(AD)/(AB)=(ED)/(CB)$