Midpoint theorem examples

Example 1

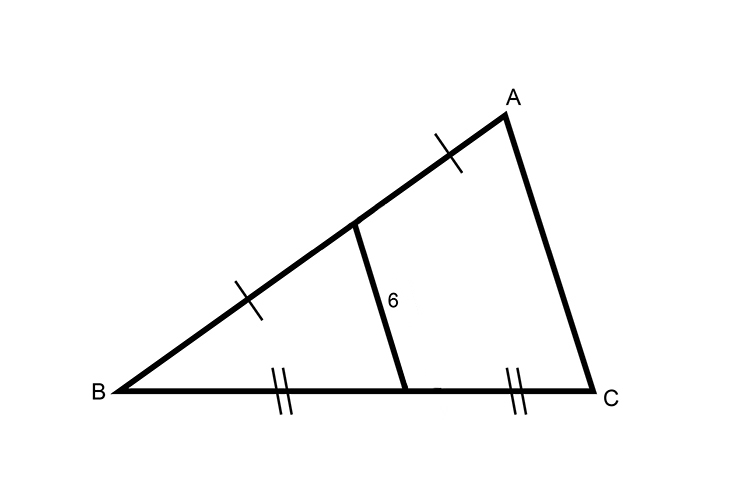
Find the distance AC

Answer follows:

The lines BC and BA are bisected at their midpoints

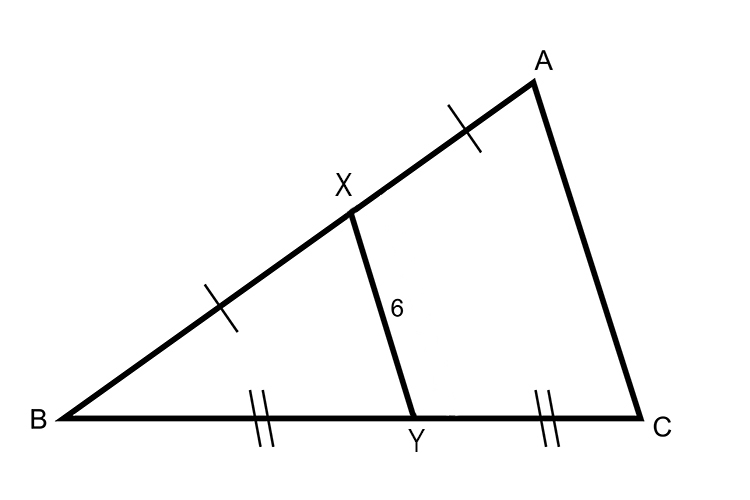
XY must therefore be parallel to AC

And midpoint theorem tells us that

XY is half the length of AC

Therefore

`AC=2times6`

`AC=12`

Example 2

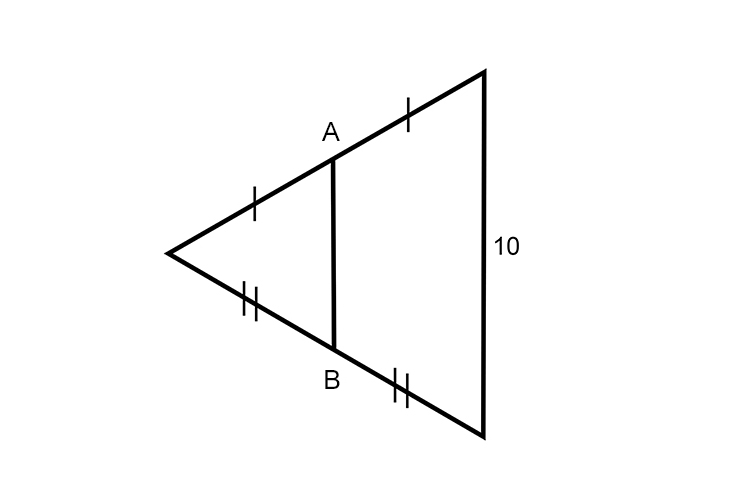
Find the distance AB

Answer follows:

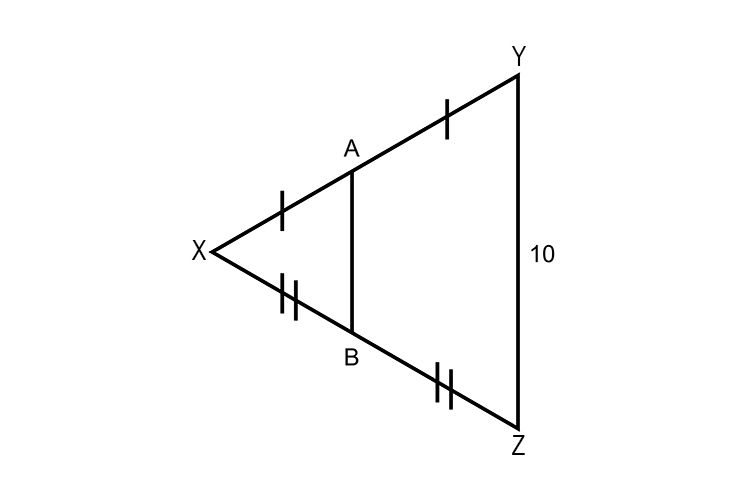
The lines XY and XZ are bisected at their midpoints

Therefore AB and YZ must be parallel

And midpoint theorem tells us that

AB is half the length of YZ

Therefore

`AB=5`

Example 3

Find the distance XY in the following diagram

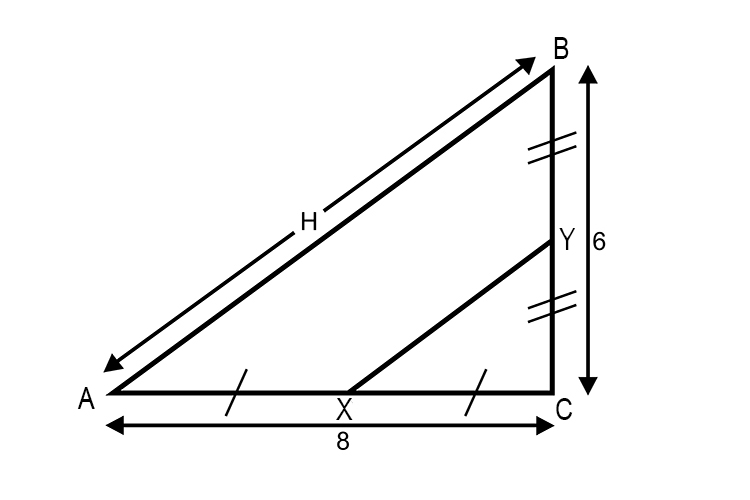
Solution

Using Pythagoras theorem `8^2+6^2=H^2`

Therefore

`H^2=64+36`

`H^2=100`

`H=10`

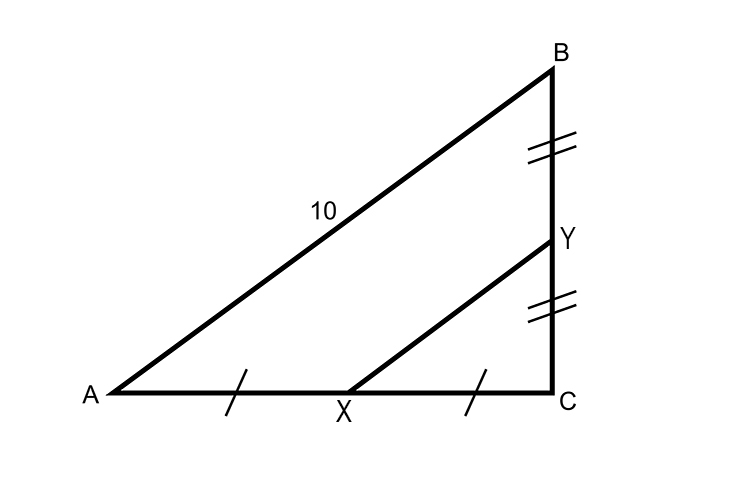
The lines AC and CB are bisected at their midpoints

XY must therefore be parallel to AB

And midpoints theorem tells us that

XY is half the length of AB

Therefore `XY` is `1/2times 10`

Answer: `XY=5`