Examples NOT using cosine rule

If the following questions came up in the exam we recommend using LOGIC to work out how to solve this problem using standard trigonometry (SOH CAH TOA) and Pythagoras.

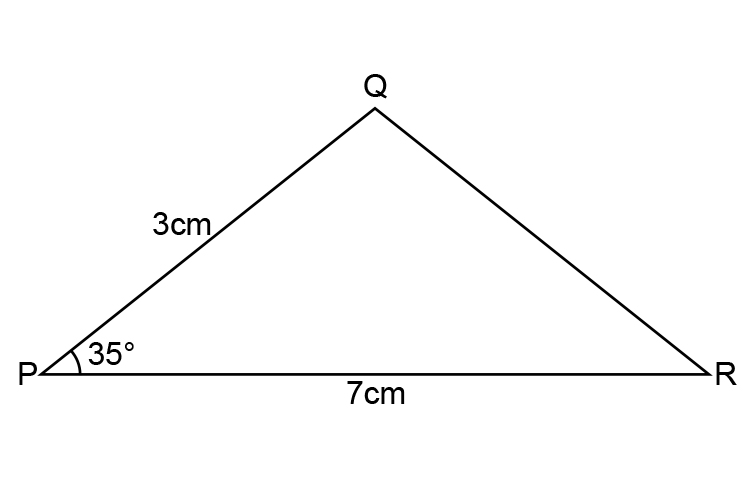
Example 1

What is the length Q to R in the following diagram?

To solve this redraw the diagram as:

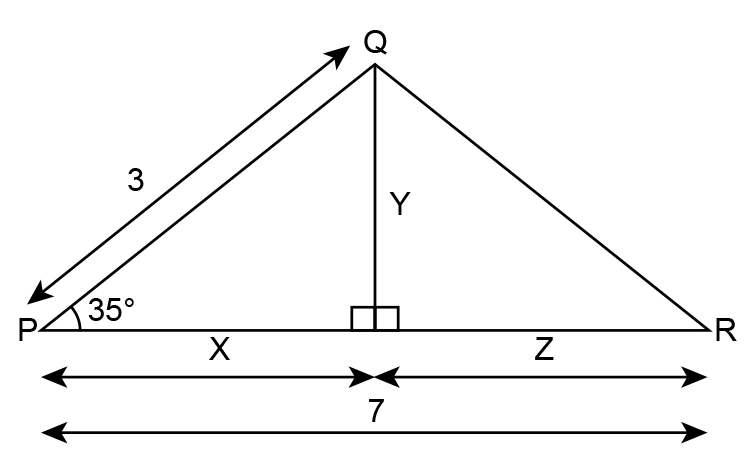
Use trigonometry (SOH CAH TOA) to find the value of `x`

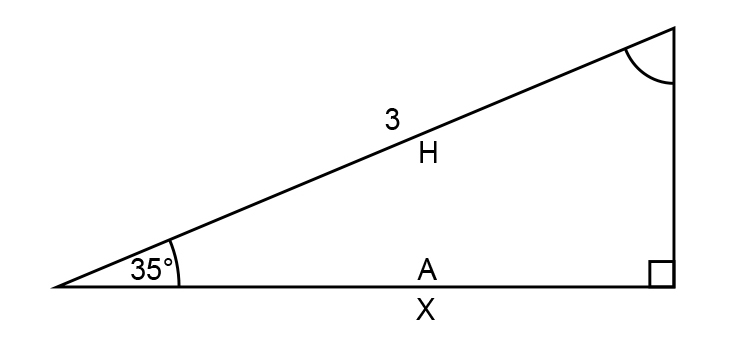
`costheta=a/H`

`cos35^@=x/3`

`x=cos35^@times3`

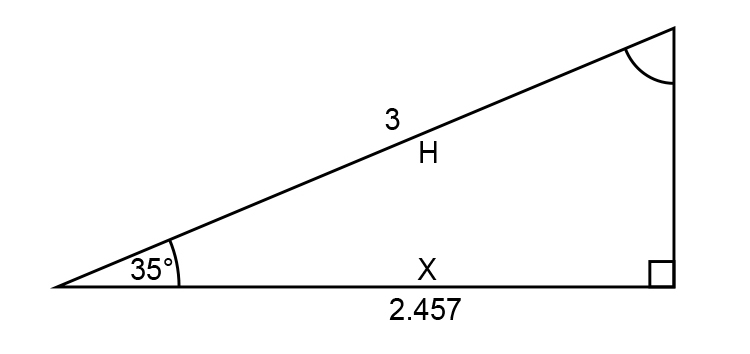
`x=0.8191times3=2.457`

`x=2.457` 

Now use Pythagoras’s theorem to find `Y`

`H^2=x^2+Y^2`

`3^2=2.457^2+Y^2`

`Y^2=3^2-2.457^2`

`Y^2=9-6.0368`

`Y^2=2.9631`

`Y=sqrt 2.9631`

`Y=1.721` 

Now find `z`

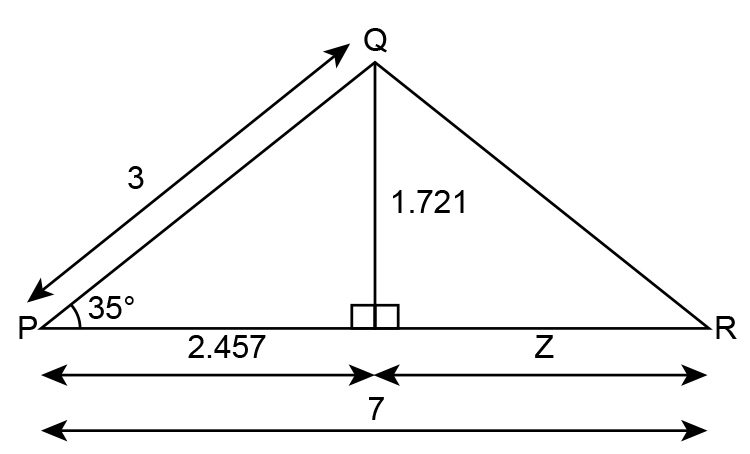
`z` is simply `7-2.457=4.543`

`z=4.543`

Then use Pythagoras’s theorem to find QR

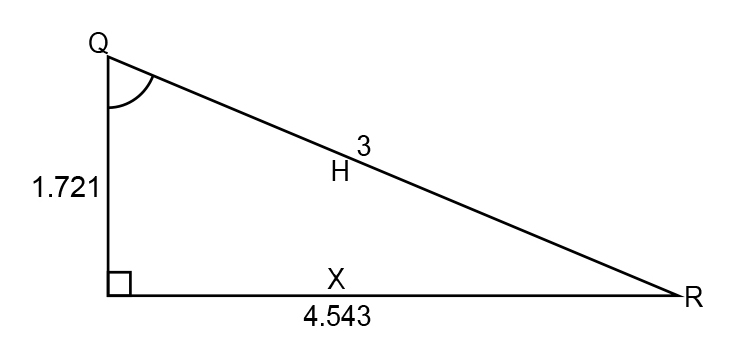
`H^2=x^2+y^2`

`QR^2=4.543^2+1.721^2`

`QR^2=20.638+2.961`

`QR^2=23.59`

`QR=sqrt 23.59`

`QR=4.58cm`

NOTE:

This may look long winded but it is incredibly logical based on the knowledge you should already have on Pythagoras and trigonometry.

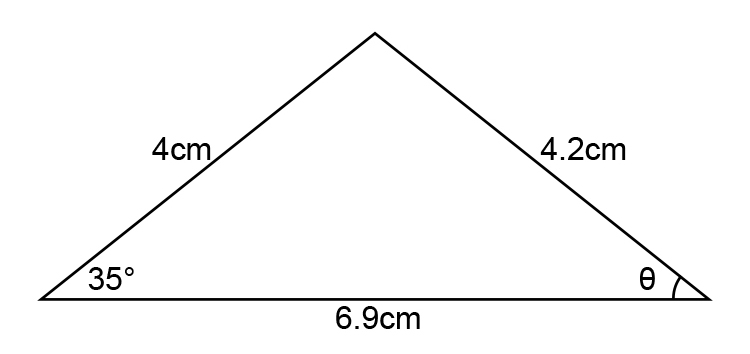
Example 2

In the diagram below find `theta`

Redraw

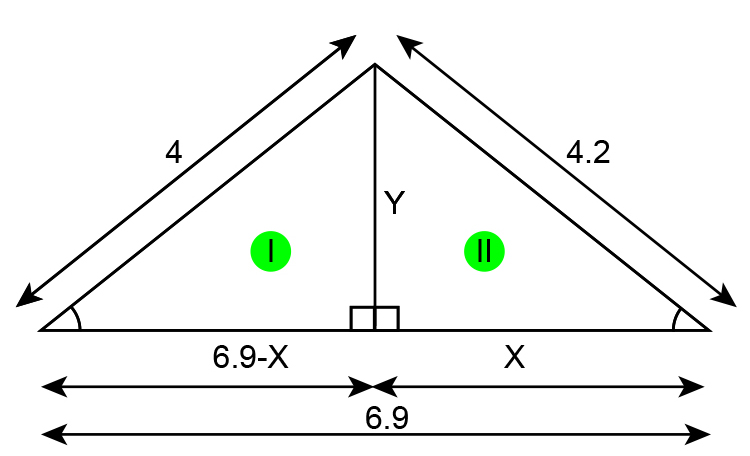
First find `x` for triangle I 

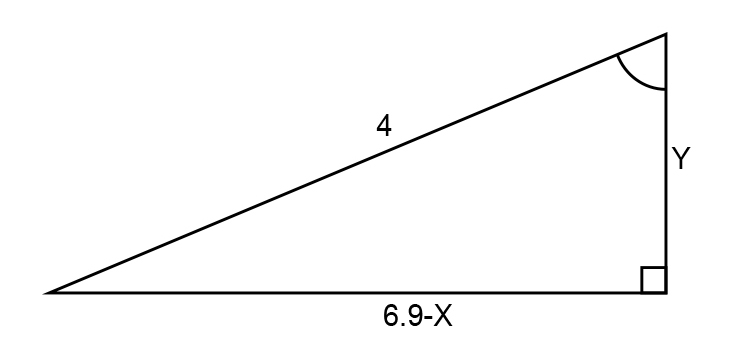
Using Pythagoras’s theorem:

`4^2=(6.9-x)^2+Y^2`

`4^2=6.9^2-6.9x-6.9x+x^2+Y^2`

`16=47.61-13.8x+x^2+Y^2`

`16-47.61+13.8x-x^2=Y^2`

`-31.61+13.8x-x^2=Y^2`…………… Equation 1

For triangle II

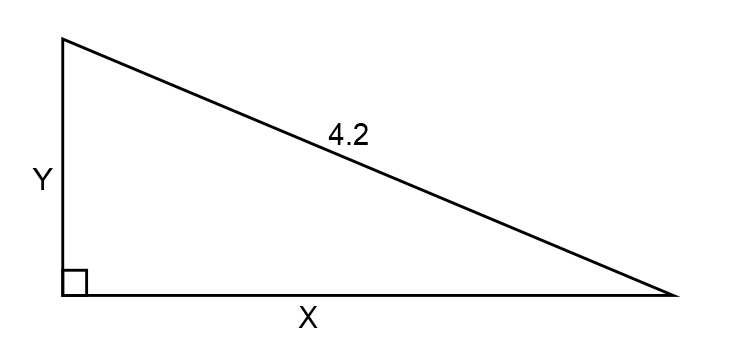
`Y^2+x^2=4.2^2`

Therefore `Y^2=4.2^2-x^2` ……………. Equation 2

Substitute equation 2 into equation 1

`-31.61+13.8x-x^2=4.2^2-x^2`

`-31.61+13.8x=4.2^2-x^2+x^2`

`-31.61+13.8x=4.2^2`

`13.8x=4.2^2+31.61`

`x=(4.2^2+31.61)/13.8`

Answer:

`x=3.56cm` long 

Now use cosine on triangle II

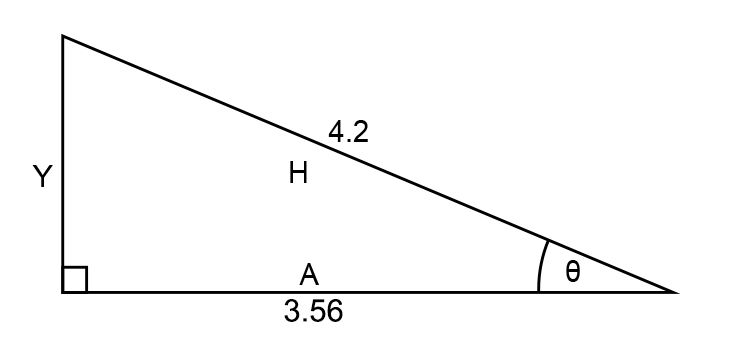
Find `theta`

`costheta=3.56/4.2`

`costheta=0.849`

`theta=31.8^@`

Again this may look long winded but the example can be completed without the need of using the cosine rule, it just takes practice.