Examples using cosine rule

Example 1

You can use the cosine rule (If you can remember it – but why try) here it is anyway:

What is the length B to C in the following diagram?

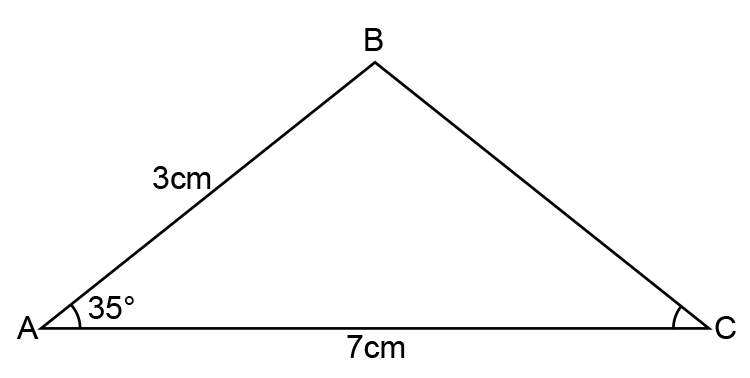
Cosine rule is:    `a^2=b^2+c^2-2bc\ cosA`

Redraw the diagram

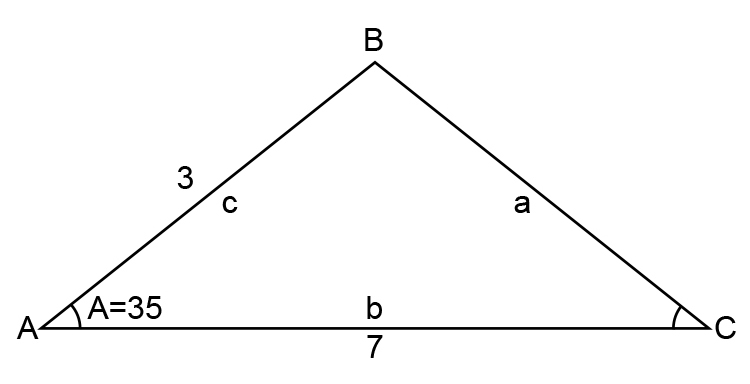
Therefore  `a^2=b^2+c^2-2bc\ cosA`

Becomes:   `a^2=7^2+3^2-2times7times3cos35^@`

`a^2=49+8-42cos35^@`

`a^2=58-42cos35^@`

`a^2=58-34.4`

`a^2=23.6`

`a=sqrt 23.6`

`a=4.85cm`

Example 2

In the diagram below find `theta`

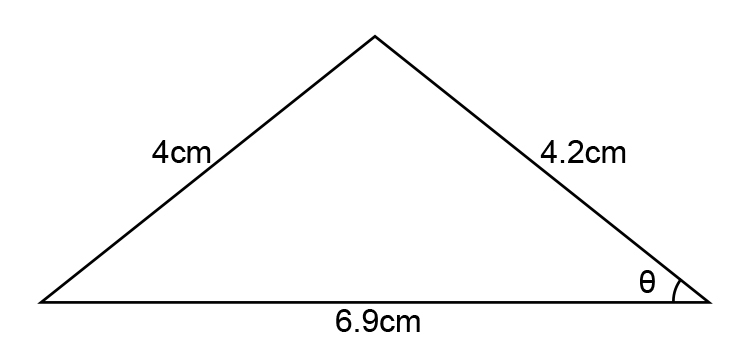
Cosine rule is:    `a^2=b^2+c^2-2bc\ cosA`

Redraw the diagram

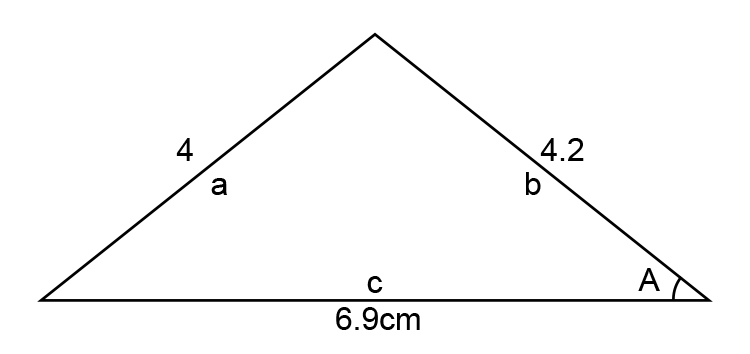
Rearrange the cosine rule:

`-cosA=(a^2-b^2-c^2)/(2bc)`

`-cosA=(4^2-4.2^2-6.9^2)/(2times4.2times6.9)`

`-cosA=(16-17.64-47.61)/57.96`

`-cosA=(-49.25)/57.96`

Swap sides to cancel out the negative

`49.25/57.96=cosA`

`0.849=cosA`

Answer: `A=31.89^@`