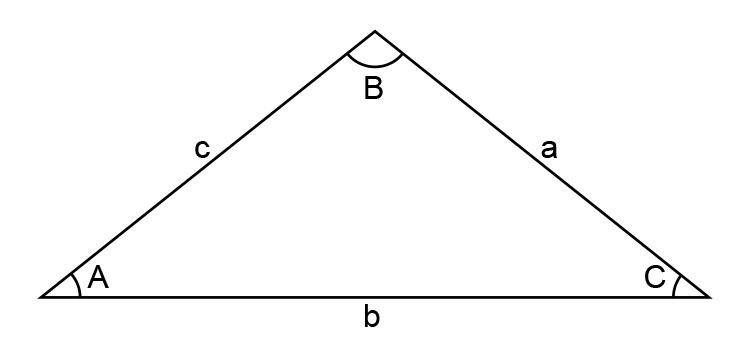
Where does the cosine rule come from?

For the mathematical puritans out there the cosine rule derives from the following:

(you really don’t need to know this)

Find “a” KNOWING the angle A and length b and c.

Redraw the diagram

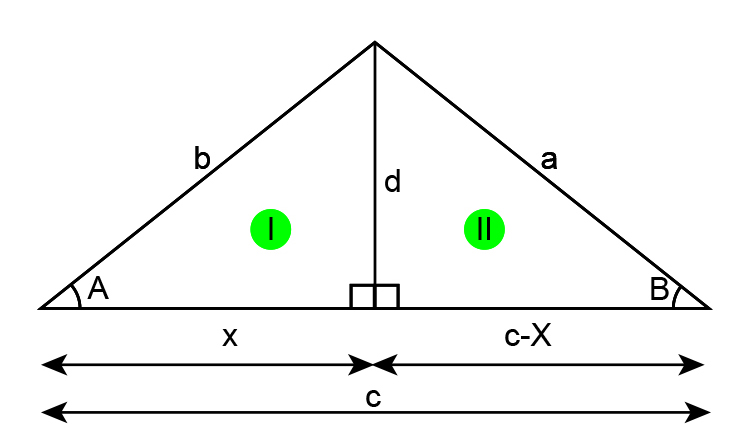
Pythagoras tells us that in triangle I ,  `x^2+d^2=b^2` ................  equation 1

Trigonometry tells us that `cosA=x/b`        

Therefore  `x=bcosA` ………… equation 2

Pythagoras also tells us that  `(c-x)^2+d^2=a^2`  …………… equation 3

Multiplying equation 3 out we get:  `(c-x)(c-x)+d^2=a^2`

`c^2-cx-cx+x^2+d^2=a^2`

`c^2-2cx+x^2+d^2=a^2` ……………. equation 4

Substitute equation 1 into equation 4 we get:

`c^2-2cx+b^2=a^2` 

Replacing `x` with equation 2 we get:

`c^2-2c(bcosA)+b^2=a^2`

Rearrange slightly

`a^2=b^2+c^2-2cb\cosA`

But again we emphasise that you really don’t need this.