Vector worked examples

Example 1

Write in terms of `a` and `b` the vector `vec (BC)`

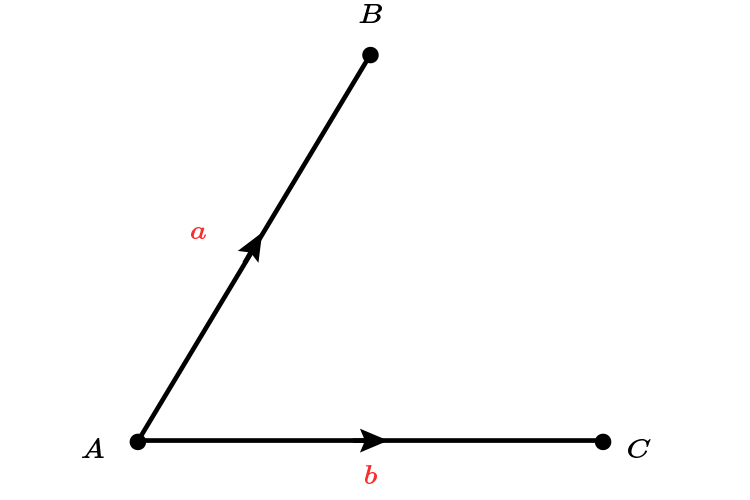
Write in terms of a and b with the following vectors

Answer as follows:

Think of this as two separate vectors

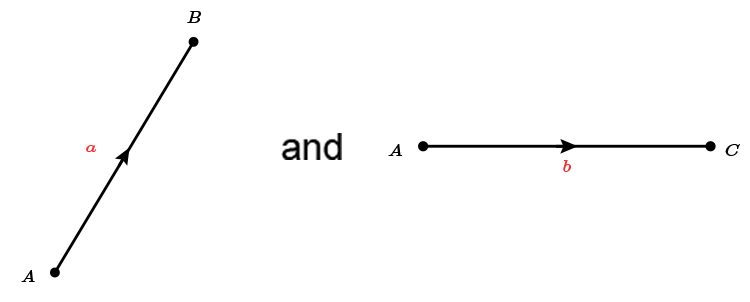
Separate the vectors in 2

Therefore

`vec (BC)=-a+b`

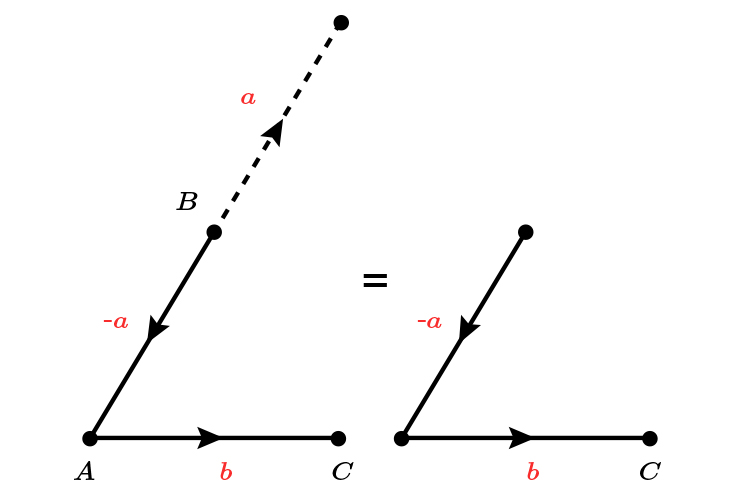
Connect up the 2 vectors and by reversing the direction of a to connect up to B

Or `vec (BC)=b-a`

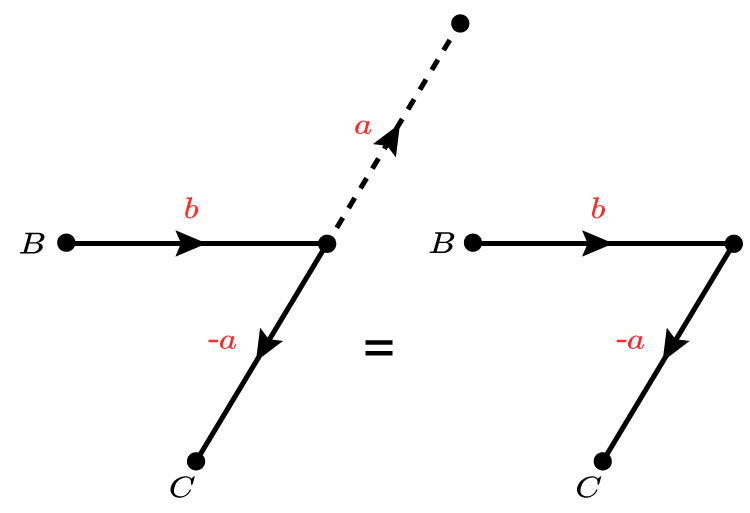
Join B with a by its end point

Example 2

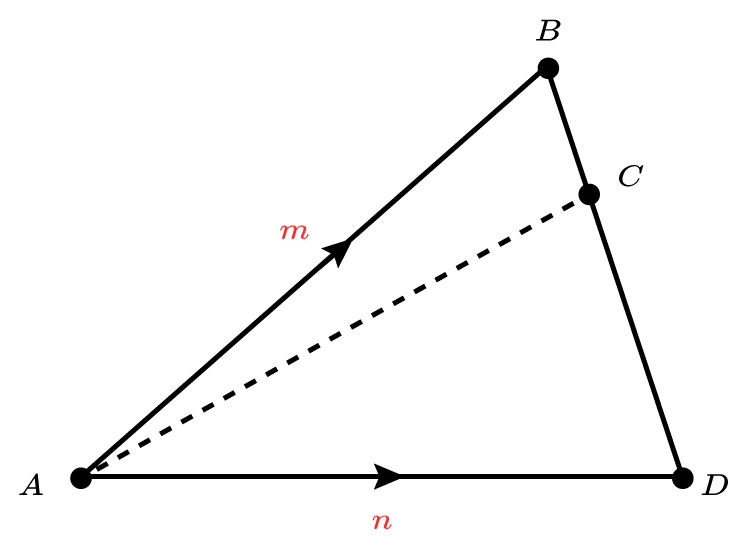
Find the line B and d with vectors M and N

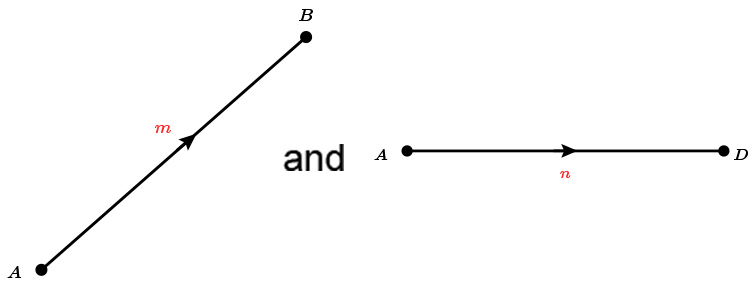
`vec (AB)=m`

`vec (AD)=n`

The point `C` on `BD` is such that:

`BC:CD=1:3`

i. Find `D` to `B` in terms of `n` and `m`

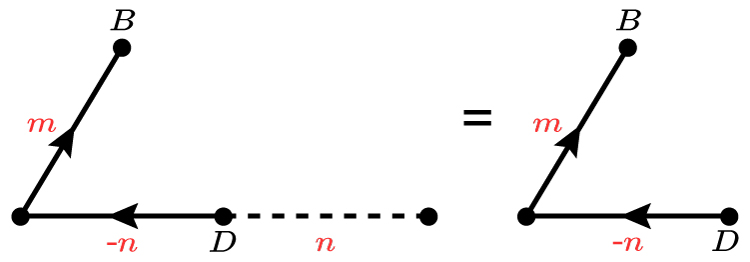
Think of this as the separate vectors

Separate the vectors in 2

Therefore

`vec (DB)=-n+m`

Reverse N so it can connect up with M

Or `vec (DB)=m-n`

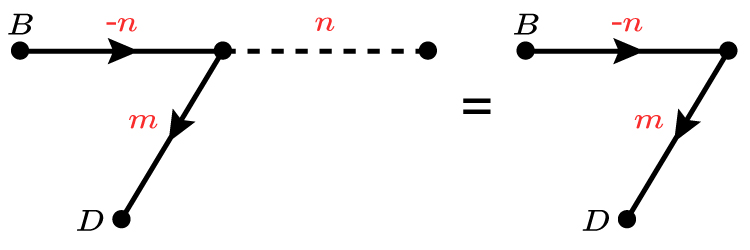
Flip the 2 vectors so n is above m

`vec (DB)=-n+m=m-n` (The latter is chosen because it's neater)

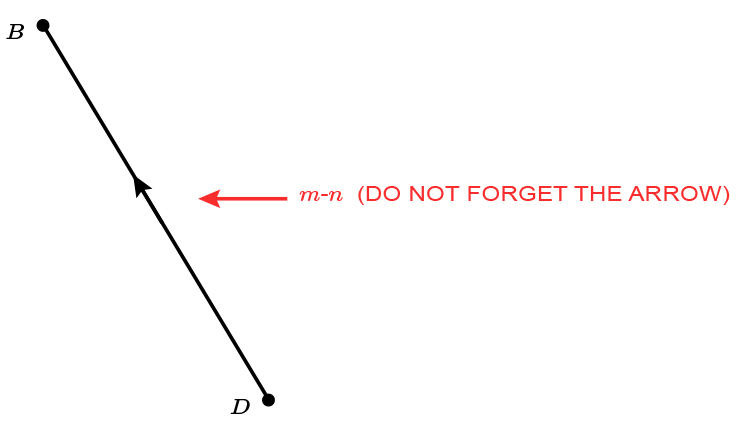
Remember don’t forget the arrow

ii. Find `vec (AC)` in terms of `m` and `n`

remember

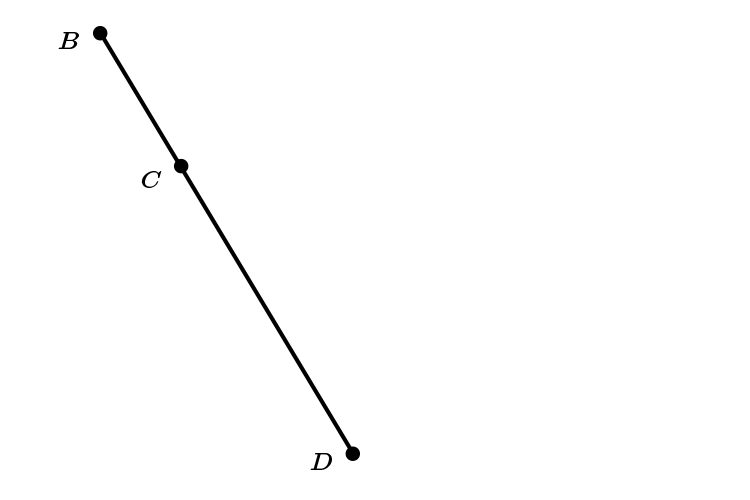
Remember the line BCD

We are told `BC:CD=1:3`

this means

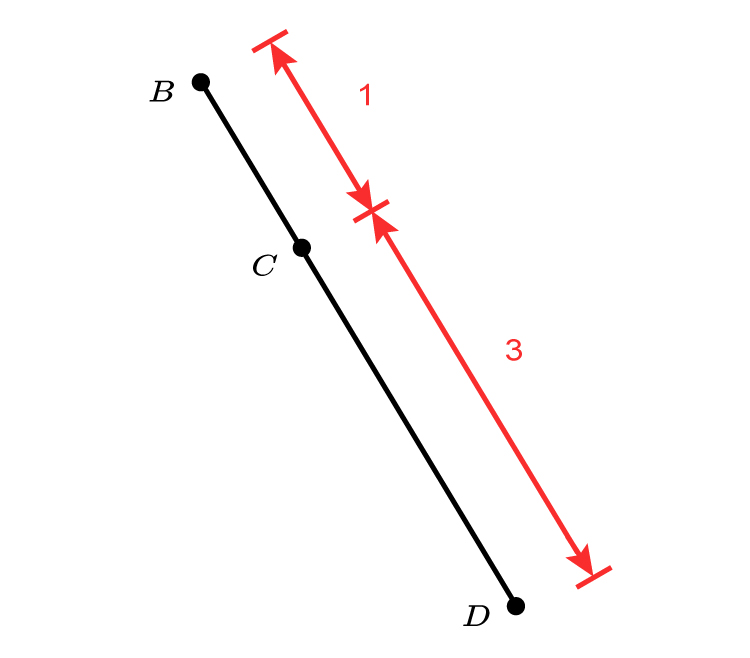
Measurements of BC and CD is 1 and 3

which also means

BC is a quarter of BD and CD is 3 quarters of BD

which also means

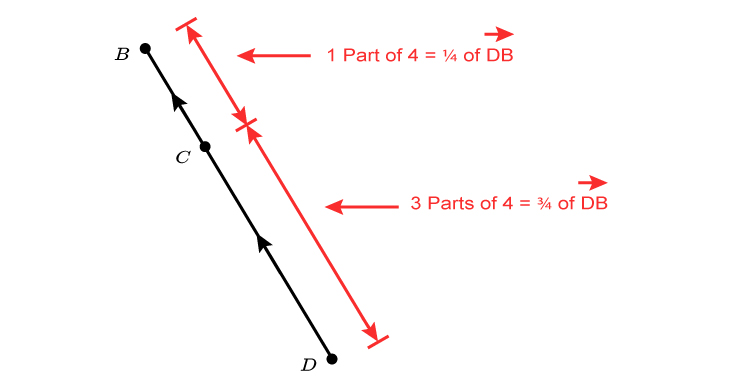
Which also means BC is a quarter n and CD is 3 quarters n

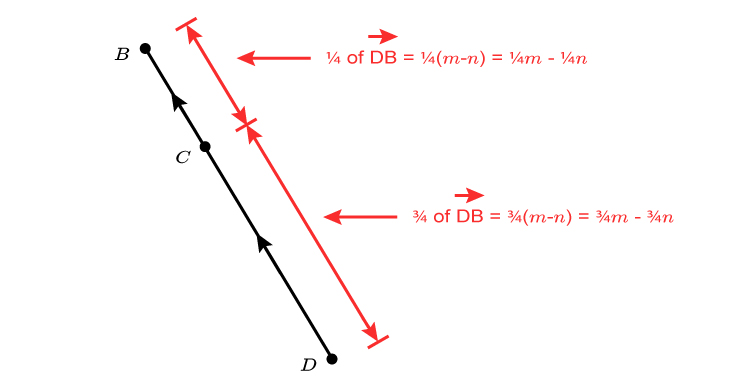
So if we redraw the original diagram

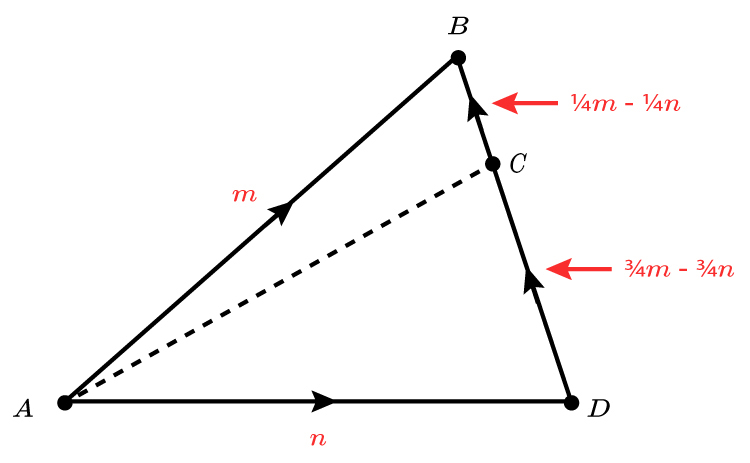
Redraw the shape showing the new vector

`vec (AC)` in terms of `m` and `n` are:

`vec (AC)=n+3/4m-3/4n`

`vec (AC)=3/4m+1/4n`

OR

`vec (AC)=m-(1/4m-1/4n)`

`vec (AC)=m+(-1times(1/4m-1/4n))`

`vec (AC)=m-1/4m+1/4n`

`vec (AC)=3/4m+1/4n`

Both get the same answer (as they should)

Answer:

`vec (AC)` in terms of `m` and `n=3/4m+1/4n`

Example 3

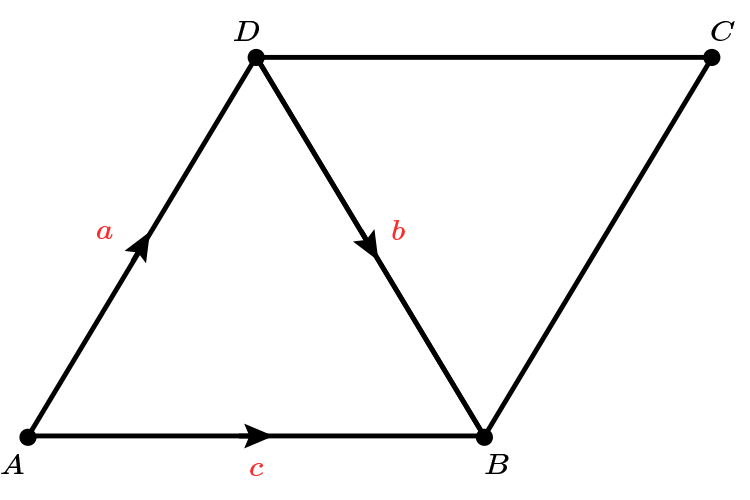
Now try this example using the parallel lines to work it out

If `AD` is parallel to `CB` and `AB` is parallel to `DC`, write in terms of `a` and `b` the vectors `vec (BC)` and `vec (BA)`

Answer as follows:

Think of this as separate vectors

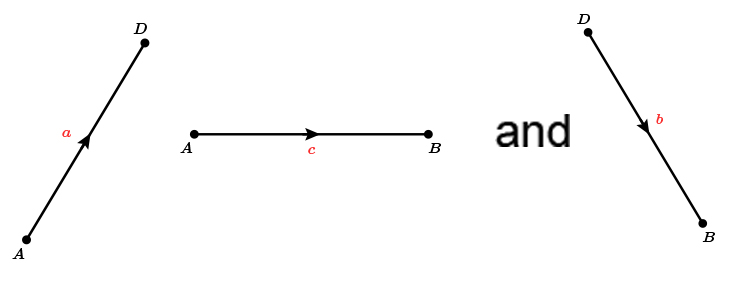
Separate the vectors

Therefore

`vec (BC)=a`

and

`vec (BA)=-c`