Gay-Lussac's Law In Use

We know in Gay-Lussac's law

`P_1/T_1=P_2/T_2`

NOTE:

Volume remains constant

Also you know that if you put a sealed container in a fire it will make the pressure inside the canister increase.

This is Gay-Lussac's law

`P_1` and `T_1` refer to the pressure and temperature before you throw the container in the fire and  `P_2` and `T_2` refer to the pressure and temperature after you throw the container in the fire.

Increasing the temperature of the gas increases the pressure in the container.

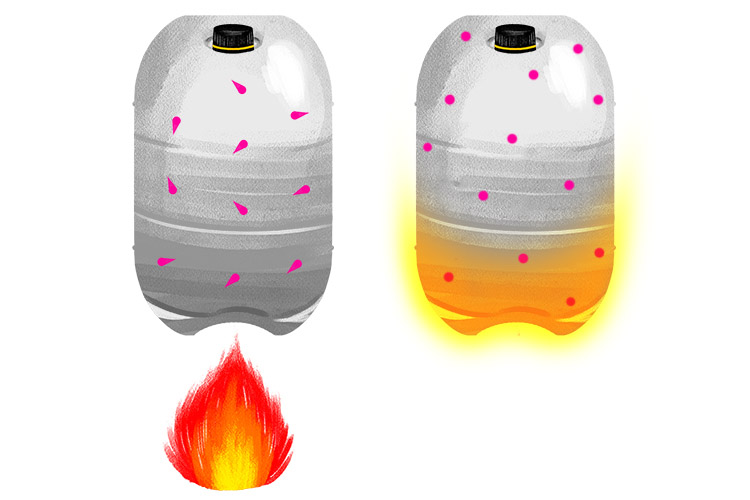
Increasing the temperature of a gas speeds up the molecules and they have more energy (kinetic energy) to hit and push the side of the container. The molecules will exert more pressure.

NOTE 1:

The standard unit used to measure pressure is `Pa` (Pascals)

The standard unit used to measure temperature is `K` (Kelvin)

NOTE 2:

You can use other units for pressure such as pounds per square inch or `mm` of mercury (mm Hg) or atm (atmospheres) as long as you use the same units either side of the equation but you must use Kelvin for temperature.

NOTE 3:

Never forget to convert temperature to Kelvin

Temperature in Kelvin `=` Temperature in degrees Celsius `(\ ^(circ)C)+273` 

You must always use temperature measured in Kelvin in any gas law equation. 

Examples

1. A `30\ \l` sample of nitrogen inside a rigid, metal container at `20^circC` is placed inside an oven whose temperature is `50^circC`. The pressure inside the container at `20^circC` was at `3.00  atm`. What is the pressure of the nitrogen after its temperature is increased to `50^circC` ?

Reveal answer

2. If a gas in a closed container is pressurized from `15` atmospheres to `16` atmospheres and its original temperature was `25^circC`, what would the final temperature of the gas be in degrees Celsius?

Reveal answer

3. The temperature of a sample of gas in a steel container at `30\ \kPa` is increased from `-100^circC` to `1.00xx10^3\ \^circC`. What is the final pressure inside the tank.

Reveal answer