Acceleration

Acceleration is a change in velocity. However it can sometimes be easier to think of it as a change in speed. How much an object accelerates depends on how quickly its velocity/speed changes.

The units for acceleration are usually metres per second per second (m/s/s) or metres per second squared (m/s²).

The formula used to calculate acceleration is:

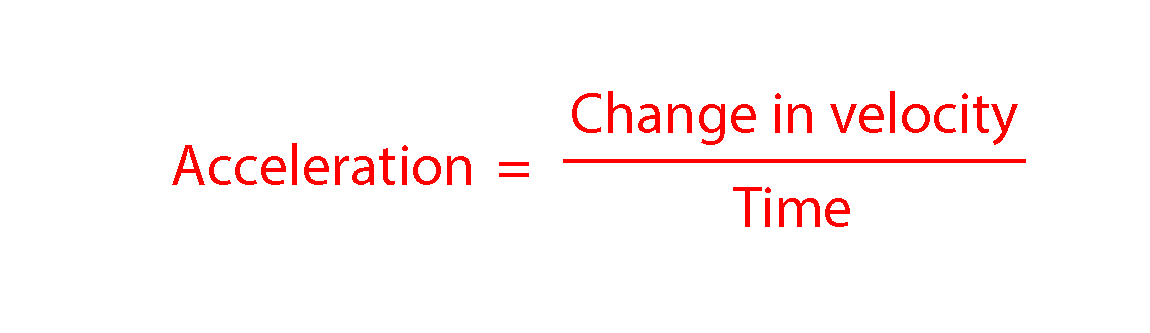
`Ac\c\e\l\e\r\ation=((v_2-v_1))/t` 

You may also see this written as

`Ac\c\e\l\e\r\ation=(Deltav)/t`    

Accelerator pedal to the floor changes speed to stay on time.

Example 1

A cyclist increases her speed from `5m//s` to `19m//s` in `7s`. What is her acceleration?

Answer:

`Ac\c\e\l\e\r\ation=(chan\g\e\ \ i\n\ \ velocity)/(time)` 

`Ac\c\e\l\e\r\ation=((19-5))/7=14/7=2\ m//s^2` 

Example 2

An oil tanker decelerates at an average rate of `0.4m//s^2`. How long to the nearest minute would it take to come to a complete stop if it was initially travelling at `12m//s`?

Answer:

`Ac\c\e\l\e\r\ation=(chan\g\e\ \ i\n\ \ velocity)/(time)` 

`-0.04=((0-12))/(time)` 

`time=((0-12))/-0.04=(-12)/-0.04=300\ \ se\c\o\nds`

`300/60=5\ m\i\n\u\tes`

Example 3

A goalkeeper takes a goal kick and the ball travels away from goal. When it reaches an opposing striker at a velocity of `12.4m//s` the ball is kicked back towards goal by the striker. This results in the ball accelerating at `72m//s^2` towards the goal for the `0.45` seconds during which the striker's foot is in contact with the ball. At what velocity does the ball leave the striker’s foot?

Answer:

`Ac\c\e\l\e\r\ation=(chan\g\e\ \ i\n\ \ velocity)/(time)` 

Multiply both sides by time to make change in velocity the subject,

`Ac\c\e\l\e\r\ationtimestime=(chan\g\e\ \ i\n\ \ velocitytimescancel(time))/(cancel(time))` 

`chan\g\e\ \ i\n\ \ velocity=Ac\c\e\l\e\r\ationtimestime` 

However there is a trick in this question! The ball is initially traveling away from goal and then accelerates towards goal, this means the acceleration is in the opposite direction and therefore is in a negative direction!

`chan\g\e\ \ i\n\ \ velocity=-72times0.45=-32.4\ m//s` 

`chan\g\e\ \ i\n\ \ velocity=v_2-v_1`

`v_2-12.4=-32.4\ m//s` 

`v_2=-32.4+12.4=-20\ m//s`

NOTE:

The velocity is negative as the direction the ball travels after the striker kicks it is opposite to the direction it was travelling when the goalkeeper kicked it.