Kinetic energy
Kinetic energy is the energy possessed by a moving object. It is calculated with the following formula:
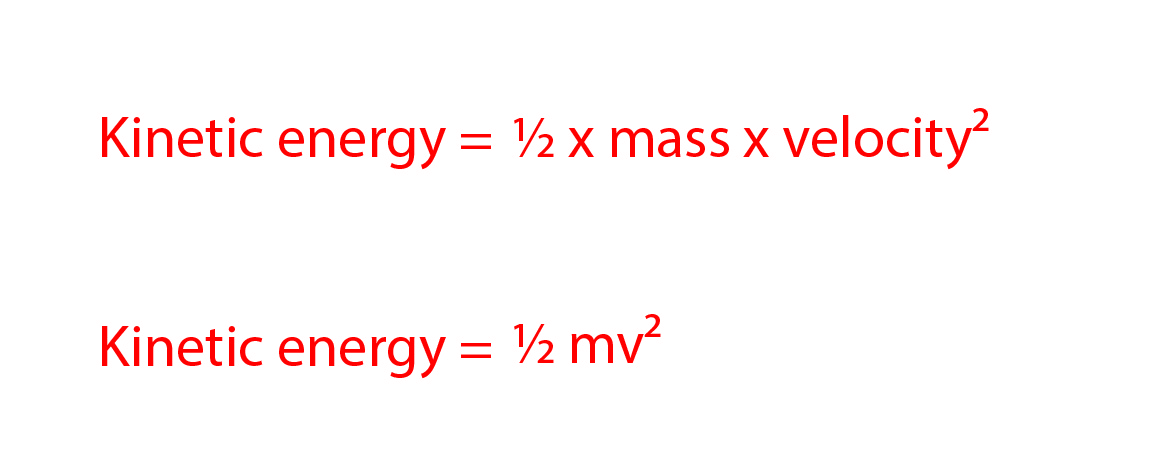

Kin had good etiquette (kinetic energy) by always leaving half the mash and vegetables for a square man.
NOTE:
Kinetic energy is directly proportional to an object's mass, so doubling the mass will double the kinetic energy at the same velocity. Kinetic energy increases with the square of an object's velocity: this means if its velocity is doubled then its kinetic energy will increase not by 2 times but 4 times the original amount. This has important implications for vehicle braking distances as the extra kinetic energy must be transformed into additional heat during braking which will increase the stopping distance. Kinetic energy is measured in Joules (J).
Example 1
What is the kinetic energy of a 1000kg car travelling at 22.5mph?
Answer
kinetic\ energy\ =\frac{1}{2}\times mass\ \times velocity2
But the velocity is in mph not standard units of m/s (metres per second) so this must be converted for use in the formula.
22.5mph = 22.5 x 1600 = 36000 metres per hour
36000 / (60x60) = 36000 / 3600 = 10 m/s
Kinetic\ energy=\frac{1}{2}\times1000\times10^2=\frac{1}{2}\times1000\times100\ =\frac{1}{2}\times100000
= 50,000 joules or 50 kilojoules (kj)
Example 2
A nail gun fires a 5g nail at 20m/s. What is the kinetic energy of the nail?
Answer
Kinetic\ energy=\frac{1}{2}\times mass\times velocity^2
But the mass is in grams, not standard units of kilograms so this must first be converted.
5g = 5/1000 = 0.005kg
Kinetic\ energy=\frac{1}{2}\times0.005\times20^2=\frac{1}{2}\times0.005\times400=\frac{1}{2}\times2=1Joule
Example 3
A cyclist and bike have a combined mass of 90kg. The cyclist pedals up to the bottom of a ramp, reaching it at a speed of 13 m/s. On reaching the bottom of the ramp the cyclist stops pedalling, by the time he reaches the top of the ramp his speed has reduced to 5 m/s.
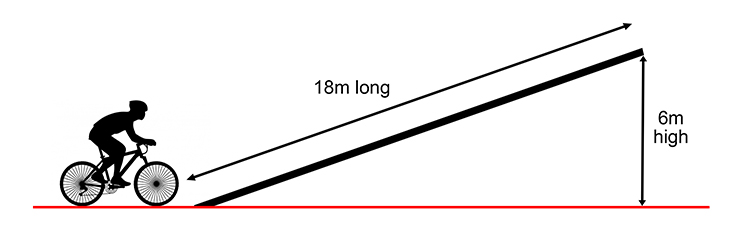
If the ramp is 18m long and 6m high, what is the kinetic energy of the cyclist and bike at the bottom of the ramp, their total energy at the top of the ramp and the energy lost due to friction as they travel up the ramp (assume acceleration due to gravity is 10m/s2).
Answer
Kinetic\ energy\ =\frac{1}{2}\times mass\ \times velocity^2
Kinetic\ energy\ =\frac{1}{2}\times90\times13^2=\frac{1}{2}\times90\times169=\frac{1}{2}\times15210=7605Joules
Total energy at the top of the ramp = Kinetic energy at top + Gravitational potential energy at the top so:
Kinetic\ energy\ at\ top\ of\ ramp\ =\frac{1}{2}\times90\times5^2=\frac{1}{2}\times90\times25=1125Joules
Gravitational potential energy = mass x gravitational field strength x height moved
GPE = mgh
Gravitational potential energy = 90 x 10 x 6 = 5400 Joules
Therefore the total energy of the cyclist and bike at the top of the ramp is:
5400 + 1125 = 6525 Joules
So the energy lost due to friction is the difference between the kinetic energy at the bottom and total energy at the top = 7605 – 6525 = 1080 Joules




