Voltage
Voltage is the electrical pressure within a circuit that causes current to flow. The formula for calculating voltage is known as Ohm’s law and is as follows
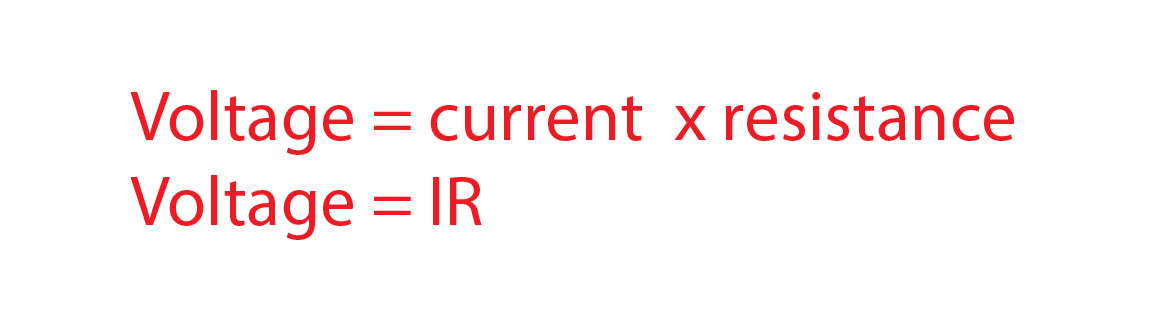

Vault (volt) into an Indian (I – current) Restaurant (R – Resistance).
NOTE:
Voltage and potential difference are the same thing and you will often see exam questions using the term potential difference instead of voltage. Voltage is measured in volts, 1 volt = 1 joule per coulomb.
Voltage (`V`) is measured in volts (`v`)
Current (`I`) is measured in Amps (`A`)
Resistance (`R`) is measured in Ohms (`Omega`)
Example 1
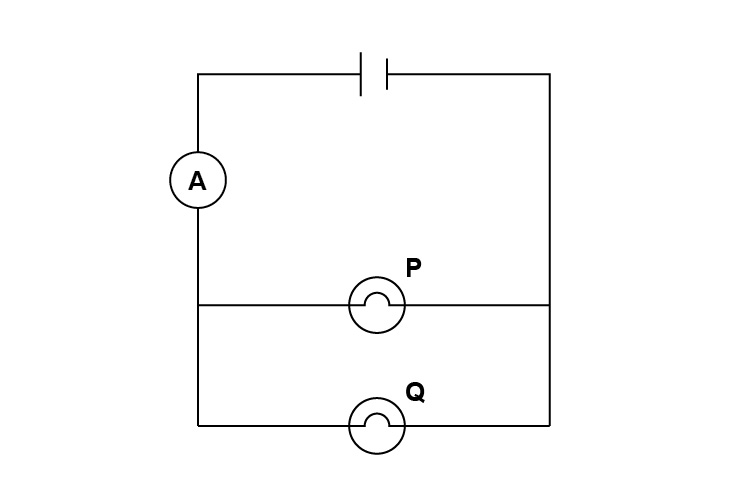
In the circuit below, lamps P and Q are identical. The reading on the ammeter is 3A. The cell shown is 6V. Calculate the resistance of lamp P.
Answer:
`V=IR` or `vo\l\t\a\g\e = currentxxre\s\i\s\t\a\nce`
Divide both sides by current to make resistance the subject,
`(vo\l\t\a\g\e)/(current)=(cancel(current)xxres\i\st\ance)/cancel(current)`
`res\i\st\ance=(vo\l\t\a\g\e)/(current)`
However, if you look at the circuit diagram you will see that the ammeter is positioned before the two lamps and they are arranged in parallel. Therefore the current that passes through lamp P is:
`(3A)/2 = 1.5A`
So the resistance of lamp P is
`res\i\st\ance=6/1.5=4Omega`
Example 2
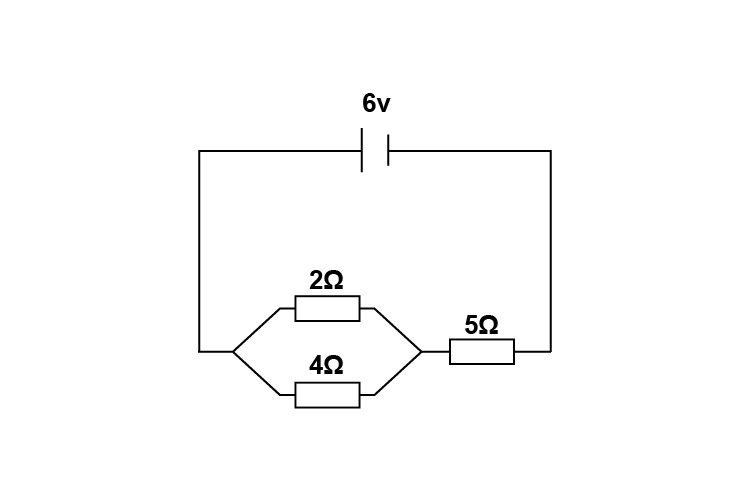
Resistors of `2` ohms and `4` ohms are connected in parallel across a battery supplying `6` volts. Another resistor of `5` ohms is connected in series with the battery. Calculate the total resistance of the circuit and the current flowing through the `5` ohm resistor.
Answer:
First you must work out the total combined resistance of the two resistors in parallel and then add the third resistor to this to get the total resistance of the circuit.
\frac{1}{R_t}\ =\frac{1}{R_1}\ +\ \frac{1}{R_2}
\frac{1}{R_t}=\frac{1}{2}\ +\frac{1}{4}=\frac{2}{4}+\frac{1}{4}=\frac{3}{4}
Therefore the total resistance of the two resistors in parallel is `4/3Omega`
So the total resistance of the circuit is `4/3Omega+5=6\1/3Omega`
The current flowing through the `5` ohm resistor can now be calculated with:
`V=IR` or `vo\l\t\a\g\e = currentxxre\s\i\s\t\a\nce`
Divide both sides by resistance to make current the subject,
`(vo\l\t\a\g\e)/(res\i\st\ance)=(currentxxcancel(res\i\st\ance))/cancel(res\i\st\ance)`
`current=(vo\l\t\a\g\e)/(res\i\st\ance)=6/(6\1/3)=0.95\ A`




