Graphs

`x` and `y` axis

The `x` axis is the horizontal axis and the `y` axis is the vertical axis.

Would you feel safer balancing the egg on the `x` or the `y`? We think you would prefer balancing the egg on X's horizontal expanse. 

And another way to remember is:

 X is a cross, so the `x` axis is across.

`x` is a cross, so the `x` axis is across. Therefore, the `y` axis is vertical.

And a further method to remember, for the poets amongst us:

X to the left, Y to the skies.

Example 1

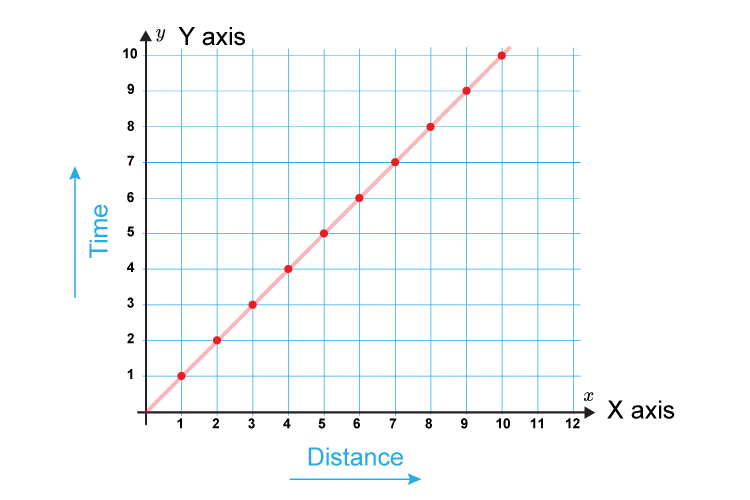
All graphs have an `x` axis and a `y` axis.

Example 2

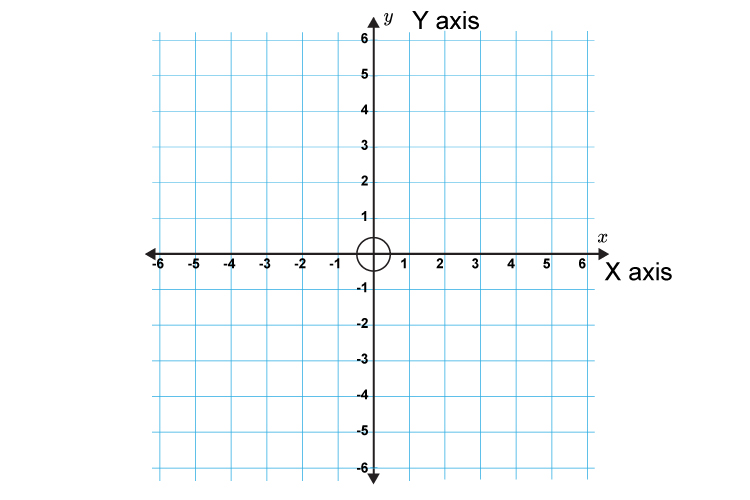
Both the `x` axis and `y` axis of a graph may also show negative values, as in the one above.