Mammoth Memory

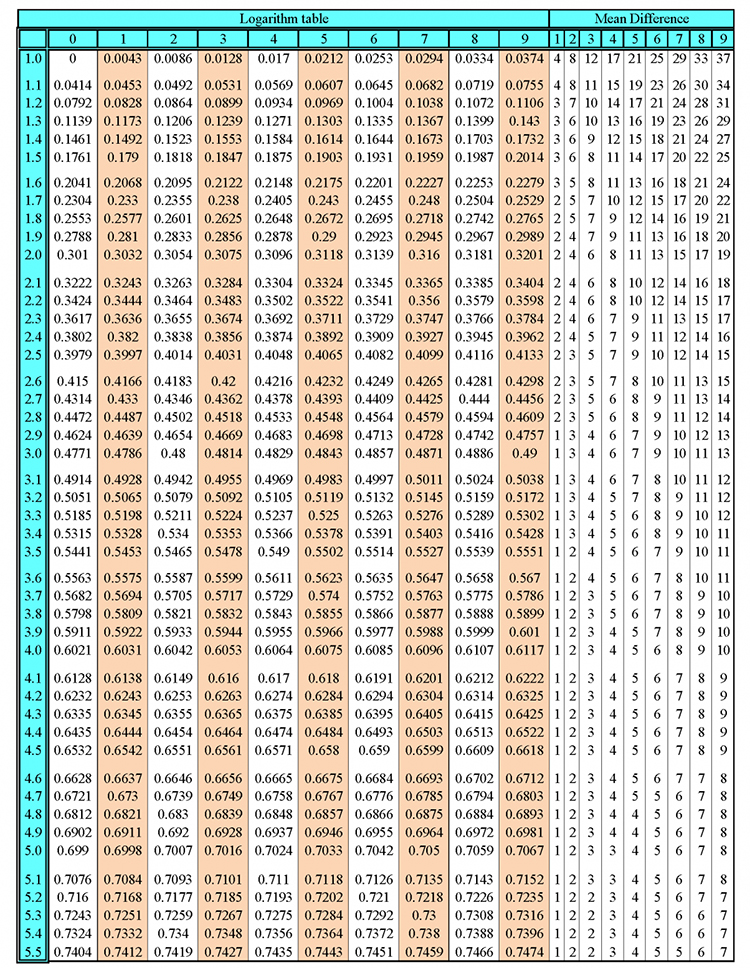
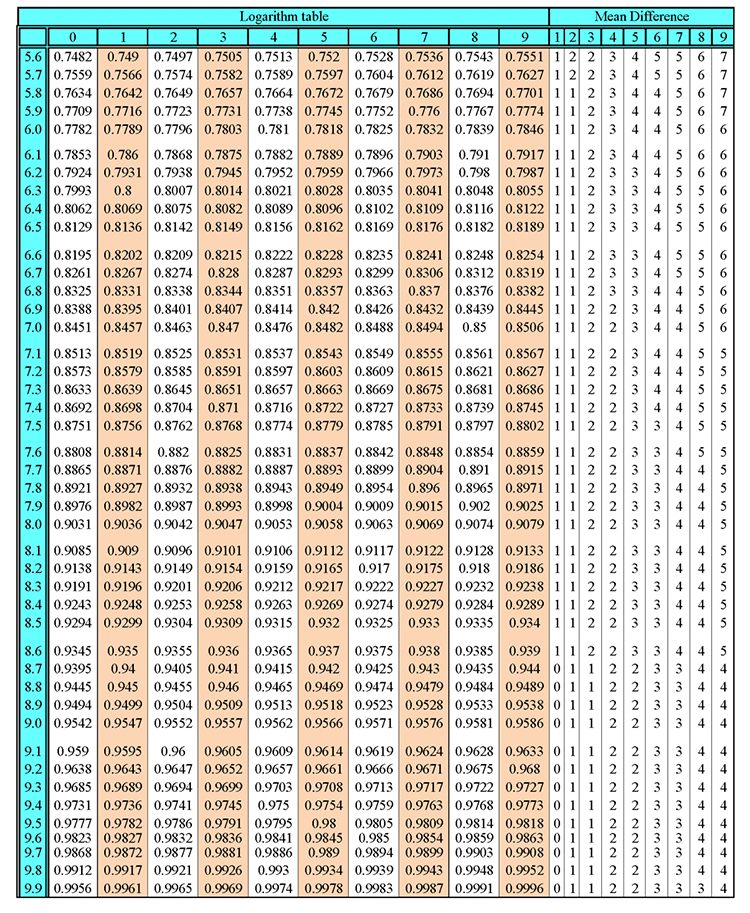
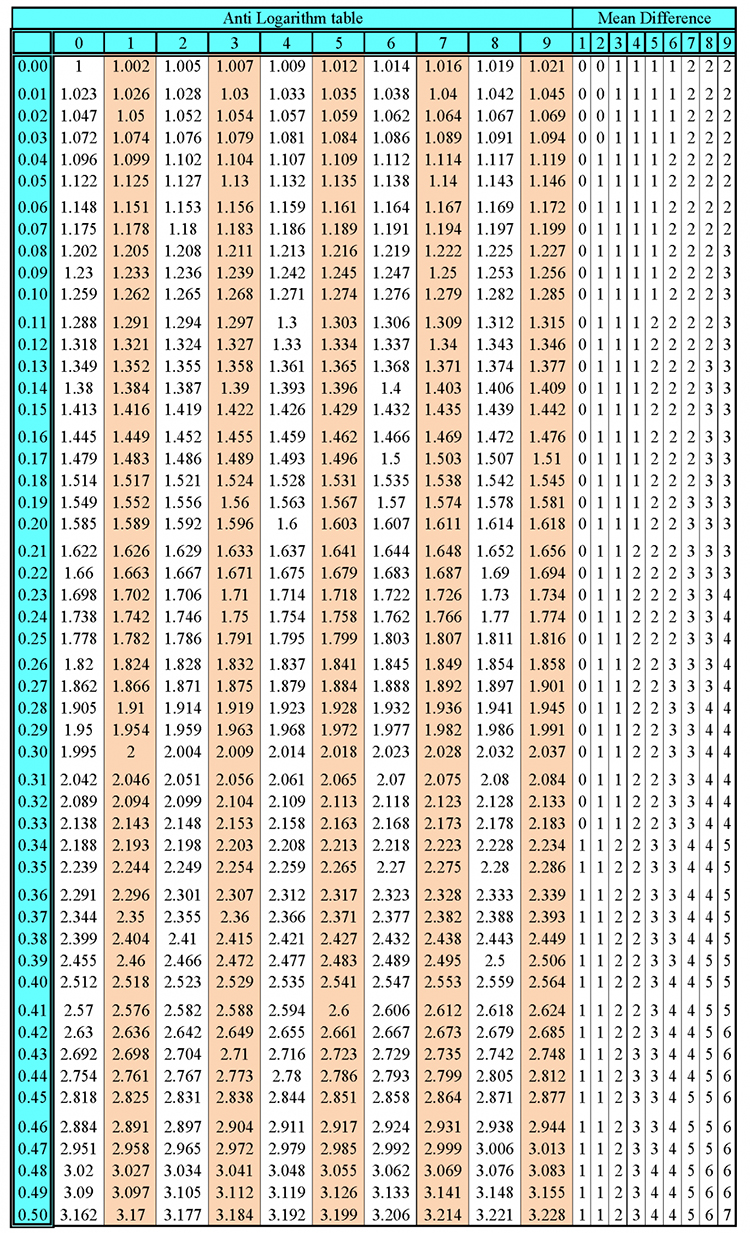
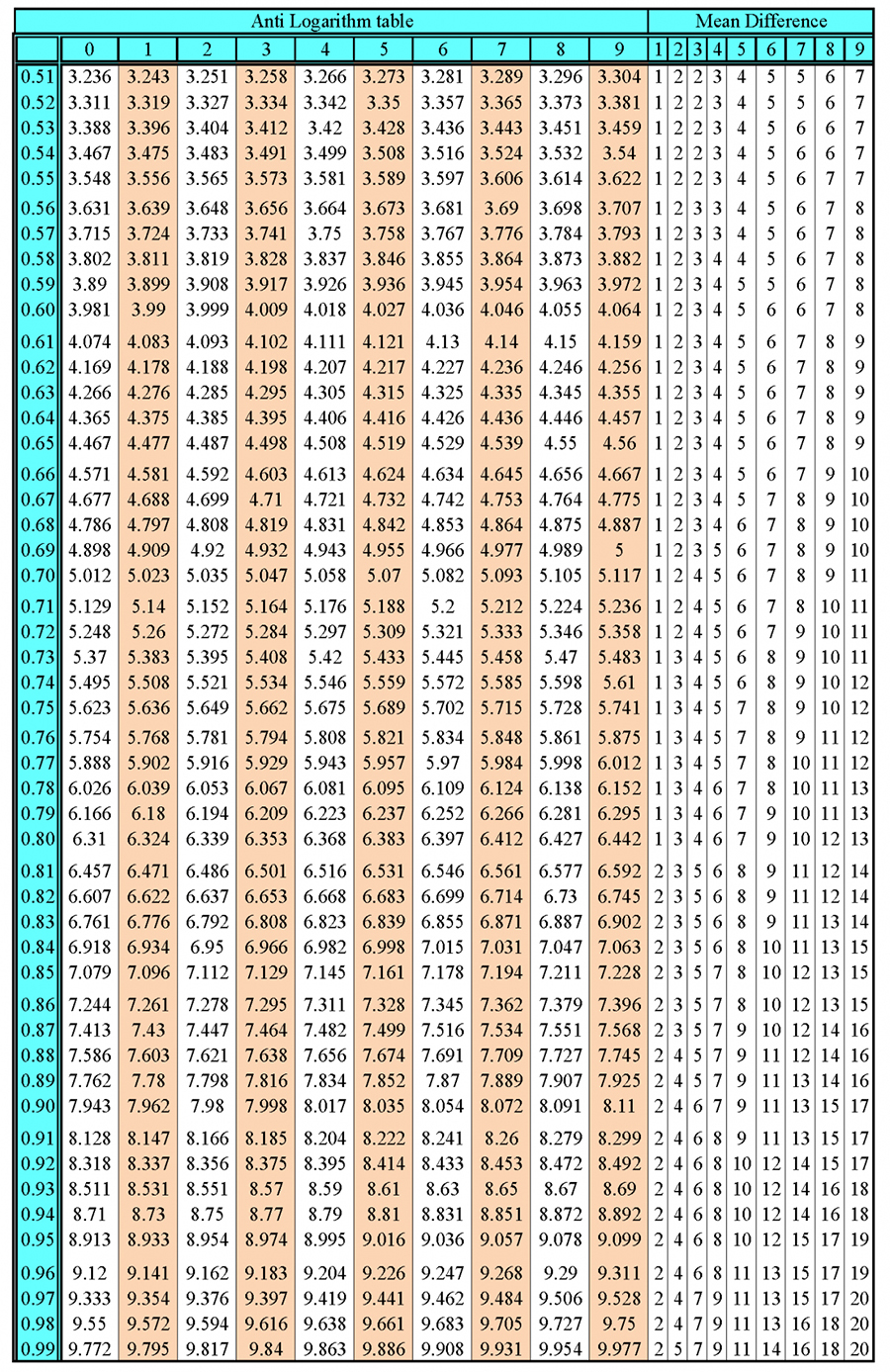
Multiplication - traditional method (long multiplication)

Is a way to multiply large numbers but you only need knowledge up to your ten times tables.

Long multiplication is the method to multiply large numbers but you only need up to your ten times tables

That’s correct. Only up to ten; Wow, that deserves a high ten.

 

Example 1

`612times24`

               
        `6` `1` `2`  
        `times` `2` `4`  
    `1` `2,` `2` `4` `0`  
  `+`   `2,` `4` `4` `8`  
    `1` `4,` `6` `8` `8`  
               

 

To see this step by step

Press Here

Multiplication - traditional method (long multiplication) step by step

Example 1

`612times24`

                   
        `6` `1` `2`   Always put the lower number lined up below the other number in their units  
        `times` `2` `4`    
                 
                   

 

                   
        `6` `1` `2`   Start by multiplying the two on the `24` but put a zero in the next line to remember it is made up of `20` not `2`    
        `times` `2` `4`    
            `0`    
                   

 

                   
        `6` `1` `2`      
        `times` `2` `4`   Now multiply the top number by `2`   
    `1` `2,` `2` `4` `0`      
                   

 

                   
        `6` `1` `2`      
        `times` `2` `4`    Now multiply the top number by `4`  
    `1` `2,` `2` `4` `0`      
      `2,` `4` `4` `8`      
                   

 

                   
        `6` `1` `2`      
        `times` `2` `4`      
    `1` `2,` `2` `4` `0`      
  `+`   `2,` `4` `4` `8`   Add `12,240` to `2,448`  
    `1` `4,` `6` `8` `8`      
                   

 

Answer: `612times24=14,688`

 

Answer: `612times24=14,688`

 

Example 2

`423times213`

               
        `4` `2` `3`  
      `times` `2` `1` `3`  
    `8` `4,` `6` `0` `0`  
      `4,` `2` `3` `0`  
  `+`   `1,` `2` `6` `9`  
    `9` `0,` `0` `9` `9`  
    `1` `1`        
               

 

To see this step by step

Press Here

Multiplication - traditional method (long multiplication) step by step

Example 2

`423times213`

                   
        `4` `2` `3`   Always put the lower number lined up below the other number in their units  
      `times` `2` `1` `3`    
                   
                   

 

                   
        `4` `2` `3`      
      `times` `2` `1` `3`   Start by multiplying the `2` of the `213` but first put two zeros on the next line to remember it is made up of `200` not `2`  
          `0` `0`    
                   

 

                   
        `4` `2` `3`      
      `times` `2` `1` `3`    Now multiply the top number, column by column, by `2`  
    `8` `4,` `6` `0` `0`    
                   

 

                   
        `4` `2` `3`      
      `times` `2` `1` `3`    Now multiply the `1` of the `213` but put one zero on the next line to remember it is made up of `10` not `1`  
    `8` `4,` `6` `0` `0`    
            `0`    
                   

 

                   
        `4` `2` `3`      
      `times` `2` `1` `3`      
    `8` `4,` `6` `0` `0`   Now multiply the top number by `1`  
      `4,` `2` `3` `0`    
                   

 

                   
        `4` `2` `3`      
      `times` `2` `1` `3`      
    `8` `4,` `6` `0` `0`   Now multiply the top number, column by column, by `3`   
      `4,` `2` `3` `0`    
      `1,` `2` `6` `9`    
                   

 

                   
        `4` `2` `3`      
      `times` `2` `1` `3`      
    `8` `4,` `6` `0` `0`   Add `84,600` to `4,230` and `1,269`  
      `4,` `2` `3` `0`    
  `+`   `1,` `2` `6` `9`    
    `9` `0,` `0` `9` `9`      
    `1` `1`            
                   

 

Answer: `423times213=90,099`

 

Answer: `423times213=90,099`

 

Example 3

`158times5`

               
        `1` `5` `8`  
        `times`   `5`  
        `7` `9` `0`  
        `2` `4`    
               

 

To see this step by step

Press Here

Multiplication - traditional method (long multiplication) step by step

Example 3

`158times5`

                 
      `1` `5` `8`      
    `times`     `5`   Always put the lower number lined up below the other number in their units  
               
                 

 

                 
      `1` `5` `8`      
    `times`     `5`   Start by multiplying `8times5` but carry over the `4` to below the line of the tens unit  
          `0`    
        `4`      
                 

 

                 
      `1` `5` `8`      
    `times`     `5`   Multiply the `5times5` but add `4` to the answer of `25` to give `29`.  Now carry over the `2` by putting it below the line of the hundreds column.   
        `9` `0`    
      `2` `4`      
                 

 

                 
      `1` `5` `8`      
    `times`     `5`   Multiply the `5times1` but add the `2` below the line to give `7`  
      `7` `9` `0`    
      `2` `4`        
                 


Answer: `158times5=790`

 

Answer: `158times5=790`

 

Example 4

`57times46`

               
          `5` `7`  
      `times`   `4` `6`  
      `2,` `2` `8` `0`  
        `2`      
        `3` `4` `2`  
          `4`    
      `2,` `6`  `2`  `2`   
        `1`      
               

 

To see this step by step

Press Here

Multiplication - traditional method (long multiplication) step by step

Example 4

`57times46`

                 
        `5` `7`      
      `times` `4` `6`   Always put the lower number lined up below the other number in their units  
               
                 

 

                 
        `5` `7`   Start by multiplying the `4` on the `46` but put the one zero on the next line to remember it is made up of `40` not `4`  
      `times` `4` `6`    
          `0`    
                 

 

                 
        `5` `7`   Now multiply the top number by `4`. The first answer is `4times7=28` but carry the two in small writing underneath the next units  
      `times` `4` `6`    
        `8` `0`    
      `2`        
                 

 

                 
        `5` `7`   Now multiply the `4times5=20` but don't forget to add the carrying unit underneath the `2` to make `22`  
    `times`   `4` `6`    
     `2,` `2` `8` `0`    
      `2`        
                 

 

                 
        `5` `7`   Now multiply the top number by `6`. The first answer `6xx7=42` but carry the `4` in small writing underneath the next unit.  
    `times`   `4` `6`    
     `2,` `2` `8` `0`    
      `2`        
          `2`    
        `4`      
                 

 

                 
        `5` `7`   Now multiply `5times6=30` but don't forget to add the carry unit underneath of `4` to make `34`  
    `times`   `4` `6`    
     `2,` `2` `8` `0`    
      `2`        
      `3` `4` `2`    
        `4`      
                 

 

                 
        `5` `7`   Now add `2,280` to `342` and ignore all the little carried numbers.
`2+0=2`
`4+8=12`
Carry the `1` in small writing underneath the next unit		  
    `times`   `4` `6`    
     `2,` `2` `8` `0`    
      `2`        
      `3` `4`  `2`    
        `4`      
        `2` `2`    
      `1`        
               
                 

 

                 
        `5` `7`  

 

 


`2+3=5`
Don't forget to add the carrying unit underneath of `1` to make `6`
`2+0=2`

  
    `times`   `4` `6`    
     `2,` `2` `8` `0`    
      `2`        
      `3` `4`  `2`    
        `4`      
     `2,` `6`  `2` `2`    
      `1`        
               
                 

 
Answer: `57times46=2,622`

Answer: `57times46=2,622`

More Info