Mean

Mean – Add up all the numbers and divide by the number of numbers.

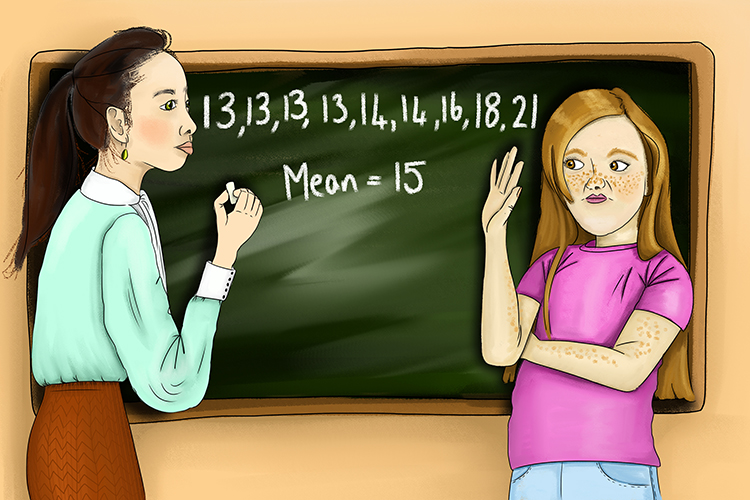
Mean is the meanest because it takes the most maths to figure it out.

This should help you remember that you add up all the numbers and divide by the number of numbers.

NOTE:

The mean is the most commonly used mathematical measure of average and is generally what is being referred to when people use the term ‘average’ in everyday language.

Example 1

`(840cm)/5=168cm` 

The mean height of these five people is 168cm. This is because when you add up all their heights;

150 + 160 + 170 + 180 + 180 = 840cm.

840 divided by the number of people is;

`(840cm)/5=168cm`  

Why is the mean used?

The mean of a set of figures is used because it is a quick method of assessing data. You don’t have to put the data in any order, but you do need to know its limitations.

Example 2

A quick way of assessing the data. Take the average using the mean for a large set of figures:

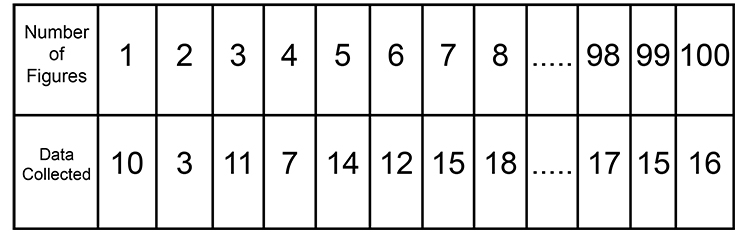
`(10+3+11+7+14+12+15+18 ...\ ...\ .17+15+16)/100` = MEAN

(this is a lot easier than median where you have to put data in order)

Example 3

The reason the mean may not be used in some situations is if one or two of the data points vary significantly from the others it can have a more significant effect on the average produced. For example:

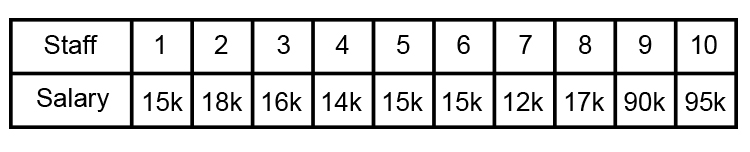
The mean salary for these ten staff is £30.7k. However, the data suggests that this mean value might not be the best way to accurately reflect the typical salary, as most workers have salaries in the £12k to £18k range. The mean is being skewed by the two large salaries. Therefore, in this situation, a better measure of central tendency would be the median.