Median
Median – Once the numbers are in order the median is the one in the middle.

The spiritual medium was in the middle, between our world and the spirits.
NOTE:
When calculating the median you must first put the numbers (or objects) in order of lowest to highest (of what your measuring), and then pick the middle number.
If there is an even number of data points, then you need to pick the two middle numbers, add them together and divide by two.
Why is the median used?
The median is particularly useful when you have a set of data where one or two points are much greater or smaller than the others. This could throw the mean off what is really a more central figure to the data, but this does not affect the median.
Example 1
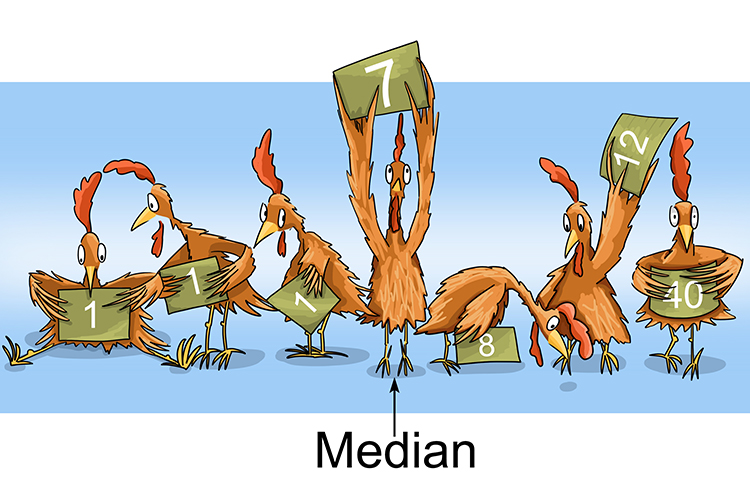
Example 2

Example 3
The number of points scored by a rugby team in each game is listed below.Calculate the median number of points this team scored.
3, 13, 7, 5, 21, 23, 39, 23, 40, 23, 14, 12, 56, 23, 29
When we put these numbers in order we have:
3, 5, 7, 12, 13, 14, 21, 23, 23, 23, 23, 29, 39, 40, 56
There are fifteen numbers. Our middle is the eighth number:
3, 5, 7, 12, 13, 14, 21, 23, 23, 23, 23, 29, 39, 40, 56
The median number of points scored is 23.
Example 4
The salaries of 8 employees are listed below
What is the median salary?
£40,000, £29,000, £35,500, £31,000, £43,000, £30,000, £27,000, £32,000
|
Solution: |
Ordering the data from least to greatest, we get: |
|
|
|
|
£27,000, £29,000, £30,000, £31,000, £32,000, £35,500, £40,000, £43,000 |
|
|
|
|
Since there is an even number of items in the data set, we compute the median by taking the mean of the two middlemost numbers. |
|
|
|
|
£31,000 + £32,000 = £63,000 |
|
|
|
|
`(£63,000)/2=£31,500` |
|
|
Answer:
The median salary is £31,500.
Example 5
Suppose you randomly selected 10 house prices in an area because you are interested in the typical house price. Priced at:
£270K, £290K, £310K, £340K, £370K, £410K, £430K, £470K, £470K, £5,080K
If we calculated the mean, we would say that the average house price is £844K. Although this number is true, it does not reflect the price of available housing in the area. A closer look at the data shows that the house valued at £5,080K (£5.08 million) skews the data. Instead, we should use the median. Since there is an even number of data-outcomes, we take the average of the middle two.
`(£370K+£410K)/2=£390K`
The median house price is £390,000. This better reflects the price house buyers should expect to pay.
Example 6
A suburb has 9 similar restaurants. Assume that a meal for two people at each restaurant costs as follows:
£60, £50, £70, £90, £80, £100, £80, £120, £110.
A few hundred meters away from these, there lies a posh Michelin stared restaurant that charges £500 for a meal for two. Now, what is the average cost of a meal for two in this locality?
The mean would be:
£60+£50+£70+£90+£80+£100+£80+£120+£110+£500 = £1260
`1260/10=£126`
If you have to find the median price, you have to sort the price in ascending order
£50, £60, £70, £80, £80, £90, £100, £110, £120, £500.
The middle value would be your median,
As there is an even number of data we take £80 + £90 as the middle two, and divide by 2:
`(£80+£90)/2=(£170)/2=£85`
The median price for a meal for two is £85. This potentially provides a more useful and accurate measure of the average meal price in the area than the mean value which is £126.




