Flat mirrors – Who can see whom – People random
In the following diagram you may be asked in an exam who can see whom. If A, B, C and D represent people standing randomly looking at the mirror, who would each person see?
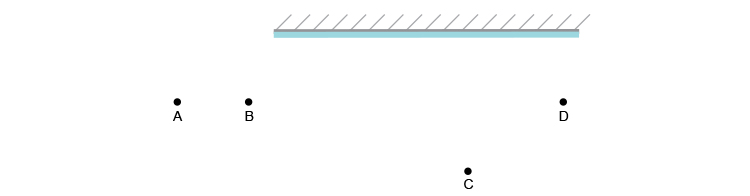
To work out who can see whom just apply the laws of reflection from each person's perspective to each of the others'.
The first stage is to draw an image on the other side of the mirror perpendicular (at 90°) to the mirror.

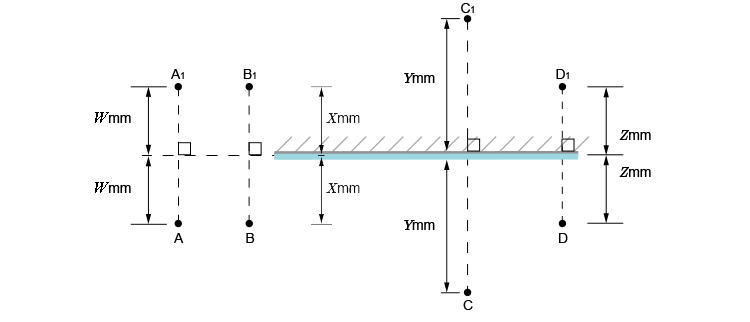
We end up with a diagram as follows:
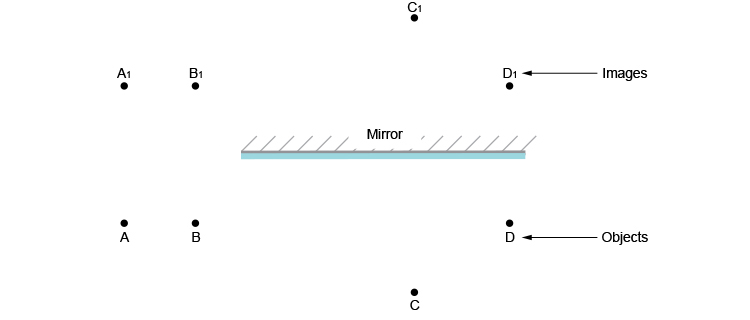
The second stage is to draw rays to person A from each of the other images of people.
We can also complete the third stage by joining the light rays from the mirror to the other people as follows:
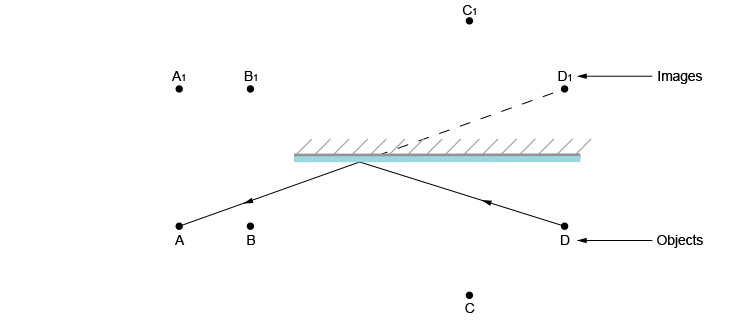
Person A can only see person D.
We can now repeat the process for person B.
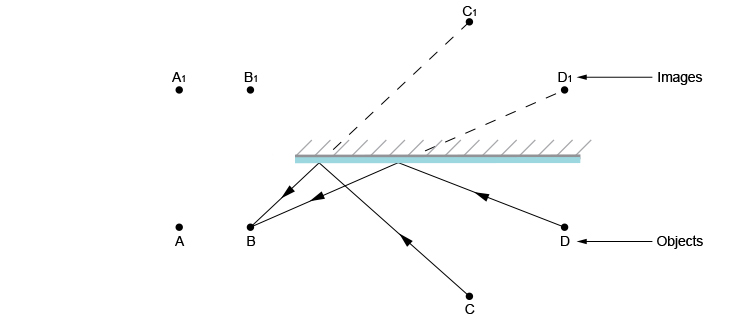
Person B can see person C and person D though the mirror.
Now let's try person C
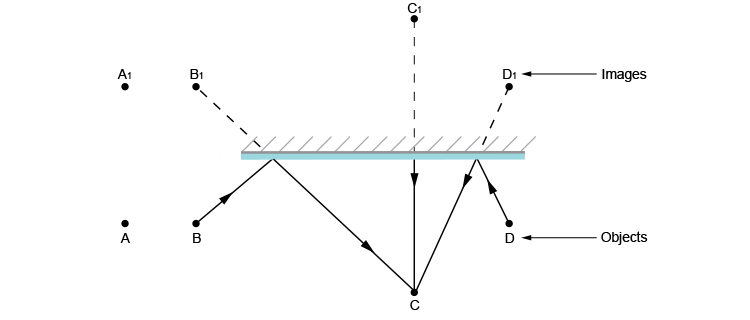
Person C can see person B, themselves and person D through the mirror.
Finally, let's find out who person D can see.
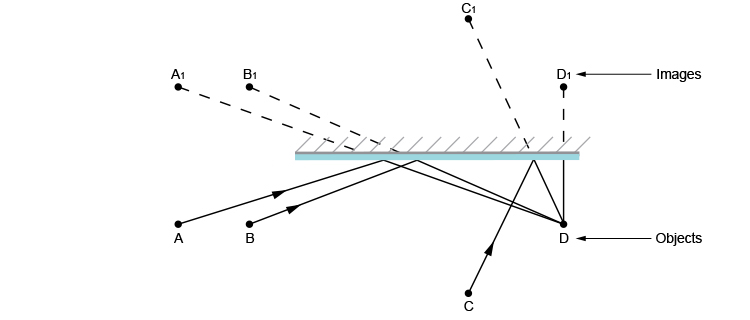
Person D can see everyone including themselves.
Summary
| Person | Can see | ||
| A | D | ||
| B | C, D | ||
| C | B, D and themselves | ||
| D | A, B, C and themselves |




