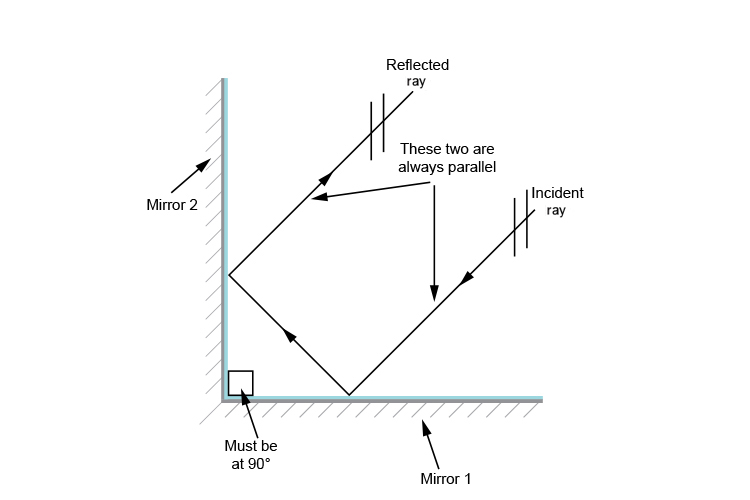
Normal line and two flat mirrors at right angles
When two plane mirrors are at right angles to each other a ray of light reflects from one mirror into the other and back out again.
The outgoing reflected ray is always parallel to the incident ray
Using the law of reflection and geometry we can show that the outgoing reflected ray is always parallel to the incident ray.
We can prove this as follows:
First of all put the normals in where the ray touches the mirrors and extend them so they meet each other.
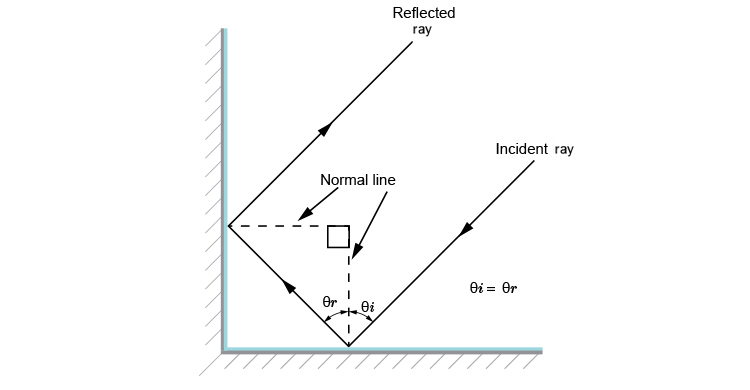
Now add the following angles.
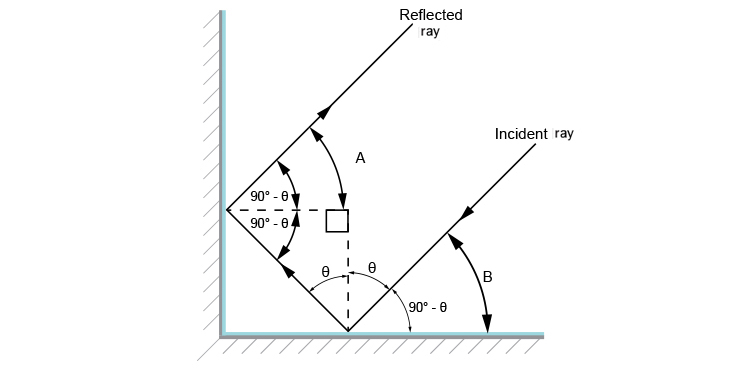
We can see that A and B equal `90^@-(m\i\n\u\s)theta`.
No matter what angle `theta` is the incident ray and reflected ray will be parallel.
Let's show you with two different angles.
Example 1
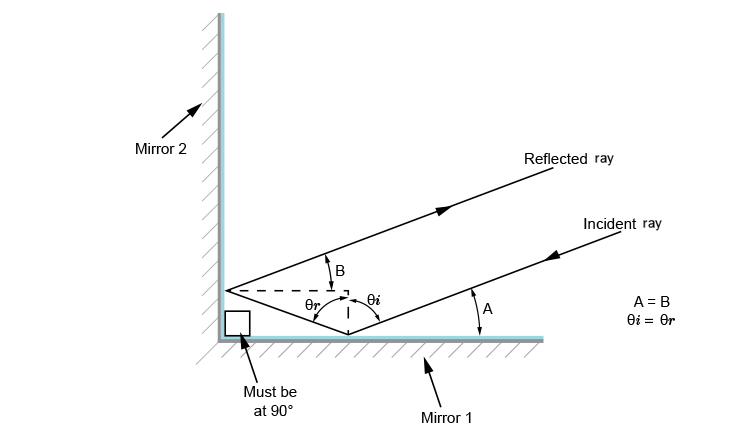
Angle A equals angle B and equal `90^@-(m\i\n\u\s)theta`
Example 2
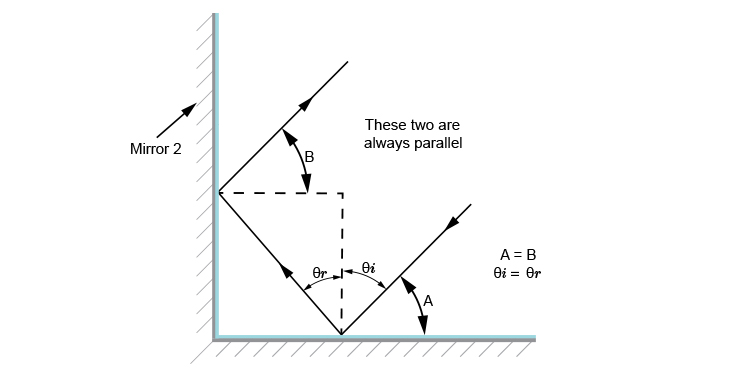
Angle A equals angle B and equal `90^@-(m\i\n\u\s)theta`




