Factorising quadratics – (difficult) (a number in front of `x^2`)

General formula for a quadratic

`ax^2+bx+c=0`

We can solve based on the fact that this is the same as

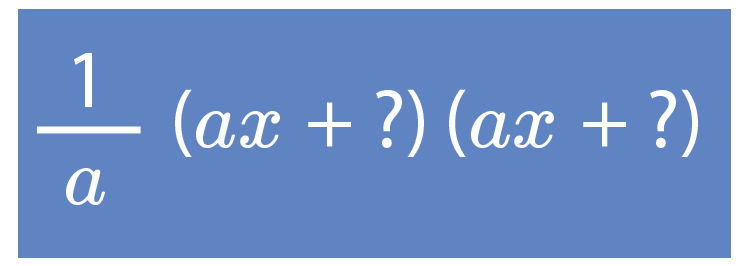
Factorising difficult examples

We must ask

What two factors of
`axxc`
add to give `b?`

Example 1

Factorise the following quadratic `4x^2-5x-6=0`

Find

What two factors of `atimesc` add up to `b`

and in this case because `atimesc=4times-6=-24`

We must ask ourselves what factors of `-24` add to give `5` :

Fill in the first ladder for negative 24, all number in the ladder need to be positive so take the negative symbol away

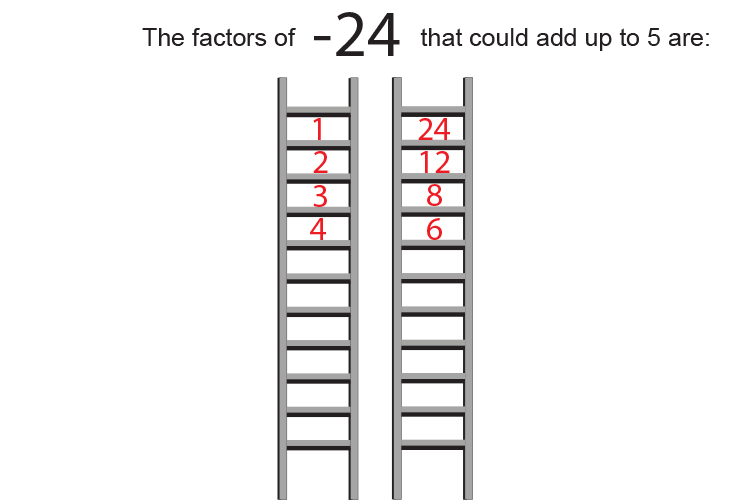
Do the same for the second ladder the resulting factors only need one negative putting against it

The factors of `-24` are:

	`1`	`times`	`-24`
`or`	`-1`	`times`	`24`
	`2`	`times`	`-12`
`or`	`-2`	`times`	`12`
	`3`	`times`	`-8`
`or`	`-3`	`times`	`8`
	`4`	`times`	`-6`
`or`	`-4`	`times`	`6`

But the only two factors that add to give `-5` are `-8` and `3`

Put this in the form

`1/a(ax+?)(ax+?)`

`1/4(4x-8)(4x+3)`

Pull out any multiples of 4 from the 1st set of brackets

`1/4times4(1x-2)(4x+3)`

`1/(cancel4)timescancel4(1x-2)(4x+3)`

`(1x-2)(4x+3)`

This can now be solved as

`1x-2=0`

and `4x+3=0`

Which is the same as

`x=2` or `x=(-3)/4`

Now check

If `x=2` `4times2^2-5times2-6=0`

`16-10-6=0` Which is correct

If `x=(-3)/4` `4times((-3)/4)^2-5times(-3)/4-6=0`

`4times((-3)/4times(-3)/4)+15/4-6=0`

`4times9/16+15/4-6=0`

`36/16+15/4-6=0`

`2\4/16+3\3/4-6=0` Which is correct

Answer:

The roots of `4x^2-5x-6=0` are `x=2` and `x=(-3)/4`

Example 2

Factorise the following quadratic `6x^2+7x-3=0`

Find

What two factors of `atimesc` add up to give `b`

and in this case because `atimesc=6times-3=-18`

We must ask ourselves what factors of `-18` add to give `7` :

Fill out the first ladder for negative 18

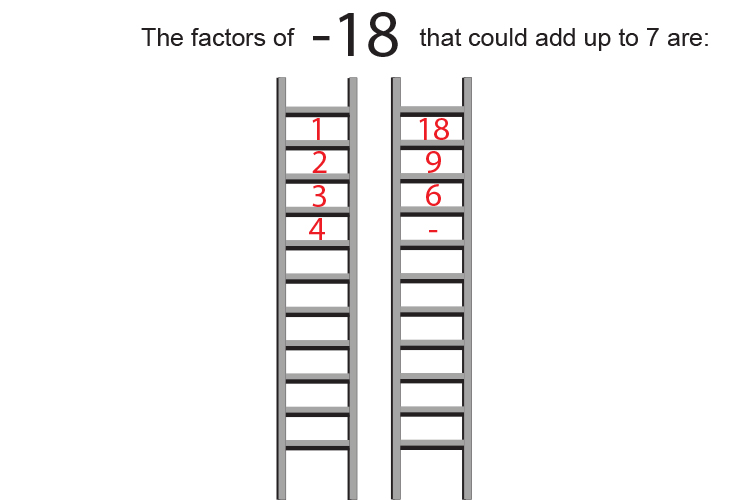
Fill out the second ladder for negative 18

The factors of `-18` are:

	`1`	`times`	`-18`
`or`	`-1`	`times`	`18`
	`2`	`times`	`-9`
`or`	`-2`	`times`	`9`
	`3`	`times`	`-6`
`or`	`-3`	`times`	`6`

But the only two factors that add to give `7` are `9` and `-2`

Put this in the form

`1/a(ax+?)(ax+?)`

`1/6(6x+9)(6x-2)`

Pull out any multiples of 6 from the 1st set of brackets

`1/6times6(1x+1.5)(6x-2)`

`1/cancel6timescancel6(1x+1.5)(6x-2)`

`(1x+3/2)(6x-2)`

This can now be solved as

`1x+3/2=0`

and `6x-2=0`

Which is

`x=-3/2`

and `x=2/6` or `1/3`

Now check

If `x=-3/2` `6times ((-3)/2)^2 +7times(-3)/2-3=0`

`6times((-3)/2times(-3)/2)-21/2-3=0`

`6times(9/4)-21/2-3=0`

`(6times9)/4-21/2-3=0`

`(3times9)/2-21/2-3=0`

`27/2-21/2-3=0`

`13\1/2-10\1/2-3=0` Which is correct

If `x=1/3` `6times (1/3)^2 +7times1/3-3=0`

`6times(1/3times1/3)+7/3-3=0`

`6/9+7/3-3=0`

`2/3+2\1/3-3=0` Which is correct

Answer:

The roots of `6x^2+7x-3=0` are `x=-3/2` and `x=1/3`

Example 3

Factorise the following quadratic `3x^2+14x-5=0`

Find

What two factors of `atimesc` add up to `b`

and in this case because `atimesc=3times-5=-15`

We must ask ourselves what factors of `-15` add to give `14` :

Fill out the first ladder for negative 15

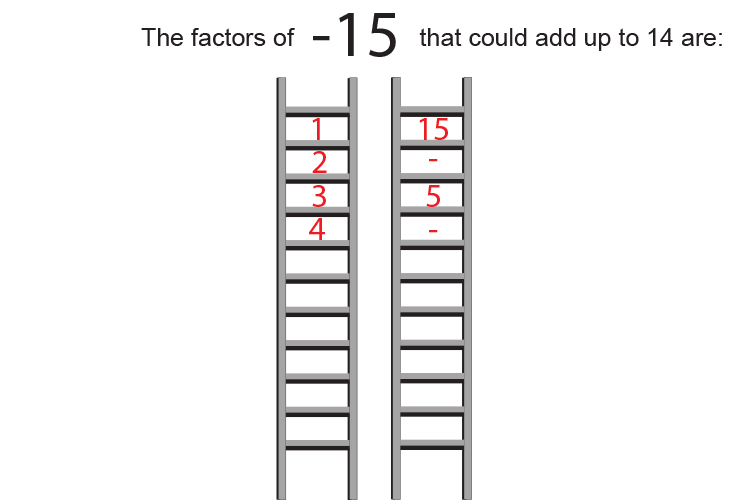
Fill out the second ladder for negative 15

The factors of `-15` are:

	`1`	`times`	`-15`
`or`	`-1`	`times`	`15`
	`3`	`times`	`-5`
`or`	`-3`	`times`	`5`

But the only two factors that add to give `14` are `15` and `-1`

Put this in the formula:

`1/a(ax+?)(ax+?)`

`1/3(3x+15)(3x-1)`

Pull out any multiples of 3 from the 1st set of brackets

`1/3times3(1x+5)(3x-1)`

`1/cancel3timescancel3(1x+5)(3x-1)`

This can now be solved as

`1x+5=0`

and `3x-1=0`

Which is

`x=-5`

and `x=1/3`

Now check

If `x=-5` `3times (-5)^2 +14times(-5)-5=0`

`75-70-5=0` Which is correct

And if `x=1/3` `3times (1/3)^2 +14times(1/3)-5=0`

`3times (1/9) +14/3-5=0`

`3/9+14/3-5=0`

`1/3+4\2/3-5=0` Which is correct

Answer:

The roots of `3x^2+14x-5=0` are `x=-5` and `x=1/3`