Factorising quadratics - (easy) Example 1

Factorise the quadratic `x^2+7x+10`

Quick sketch

Factorise 10 in this case as it is the only whole number fill in the first ladder

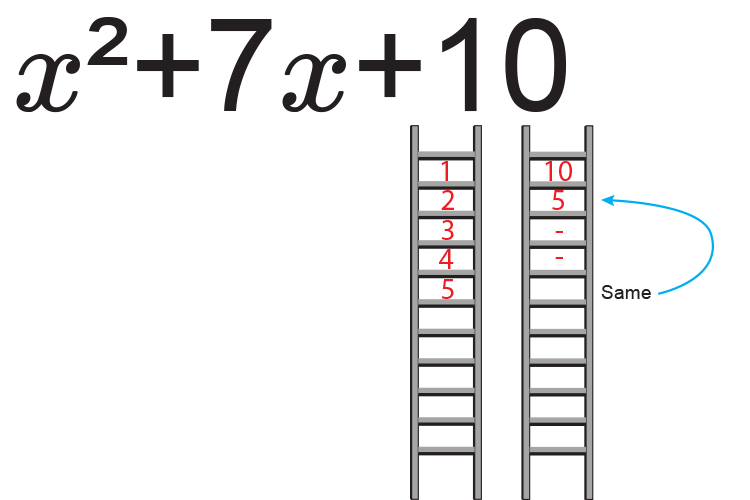
Find factors on the second ladder for 10

Therefore the factors of 10 are:

1 and 10

2 and 5

Now ask yourself what factors of `c` add to give `b`.

i.e. what factors of 10 equal 7.

`5times2=10` `5+2=7`

Therefore:

`x^2+7x+10`

Can be written as:

`(x+2)(x+5)`

Check by multiplying out:

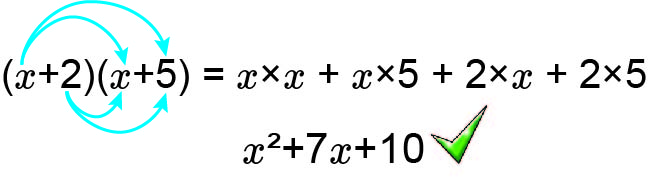
Put the factors in an equation and multiply out

The shock is that `(x+2)(x+5)` also gives you the roots of `x^2+7x+10=0`

Separate the brackets and put them equal to zero.

`x+2=0`

And `x+5=0`

Now solve for `x`

Therefore `x=-2` and `x=-5`

Answer:

The roots of `x^2+7x+10=0` are `x=-2` and `x=-5`

NOTE:

This example has also been used in completing the square examples and quadratic formula examples to show that the roots `-2` and `-5` can be found using any of these methods.