Standard form divide
To divide in standard form all you need to remember is that
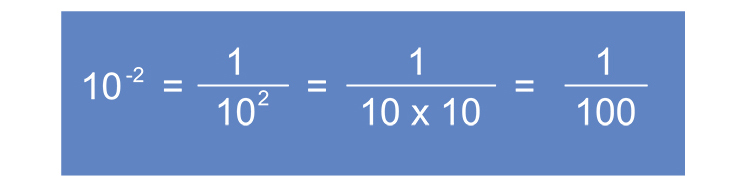
NOTE:
See indices Mammoth memory for further explanation
But the basis of divide in standard form is first look for a simple comparable that you know with indices.
i.e. try simple numbers you know first
Example 1
Work out the following giving your answer in standard form
`44800div6.4times10^9`
Method 1
Actually carry out the division
`44800div6.4times10^9`
is the same as
`44800div6.4times10times10times10times10times10times10times10times10times10`
which is
`44800div6,400,000,000`
which is
`(448cancel0cancel0)/(6,400,000,0cancel0cancel0)`
`448/(64,000,000)`
`=0.000007`
and to put this in standard form
remember move decimal right and `-1` to the power
Answer: is `=7times10^-6`
Method 2
An alternative way to calculate this is to say what is a simpler calculation, what is
`10^2div10^3`
`=(cancel10timescancel10)/(10timescancel10timescancel10)=1/10`
`=10^-1`
Therefore
`44800div6.4times10^9`
is the same as
`4.48times10^4div6.4times10^9`
`(4.48times10^4)/(6.4times10^9)`
`4.48/6.4times10^4/10^9`
`0.7times10^-5`
and in standard form this is
remember move decimal right and `-1` to the power
Answer: is `7times10^-6`
Example 2
Work out the following giving your answer in standard form
`(1.4times10^12)div(3.2times10^4)`
Method 1
Actually carry out the division
`1.4times10^12=1.4times10times10times10times10times10times10`
`times10times10times10times10times10times10`
`=1,400,000,000,000`
and
`3.2times10^4=3.2times10times10times10times10`
`=32,000`
So the calculation becomes
`(1,400,000,000,cancel(000))/(32,cancel(000))`
`=(1,400,000,000)/32`
`=43,750,000`
and to put this in standard form
remember move decimal place left and `+1` to the power
Answer is `=4.375times10^7`
Method 2
An alternative way to calculate this is to say what is a simpler calculation, what is
`10^2div10^3`
`=(cancel10timescancel10)/(10timescancel10timescancel10)=1/10=10^-1`
Therefore:
`(1.4times10^12)div(3.2times10^4)`
is the same as
`(1.4times10^(cancel(\ 12)8))/(3.2timescancel10^cancel(\ 4))`
`(1.4times10^8)/3.2`
`=0.4375times10^8`
remember move decimal place to right and `-1` to the power
and to put this in standard form this becomes
`4.375times10^7`
Example 3
Work out the following giving your answer in standard form
`(3.8times10^8)div(1.9times10^-3)`
Method 1
Actually carry out the division
`(3.8times10^8)div(1.9times10^-3)`
is the same as
`3.8times10times10times10times10times10times10times10times10div1.9/(10times10times10)`
which is
`380,000,000div0.0019`
which is
`(380,000,000)/0.0019`
`=200,000,000,000`
and to put this in standard form
remember to move decimal place left and `+1` to the power
Answer: is `2times10^11`
Method 2
An alternative is to find a similar calculation that you know. In this case
`10^2div10^-2`
`=1000div0.1`
`=1000/0.1=10,000`
or similarly
`10^2div10^-2`
is
`10^2div1/10^2`
`=10^2/(1/10^2)`
`=10^2times10^2`
`=10^4`
`=10,000`
Now to the actual calculation
`(3.8times10^8)div(1.9times10^-3)`
would be
`(3.8times10^8)div(1.9/10^3)`
`=(3.8times10^8)/(1.9/10^3)`
`=(3.8times10^8times10^3)/1.9`
`=(3.8times10^11)/1.9`
`=2times10^11`
which is already in standard form so the answer is `=2times10^11`




