Opposites divided by adjacent and the world of Tan

NOTE:

Only look at this if you want to know where cosine comes from.

Mathematicians built a world of right-angled triangles where the hypotenuse was always 1m long.

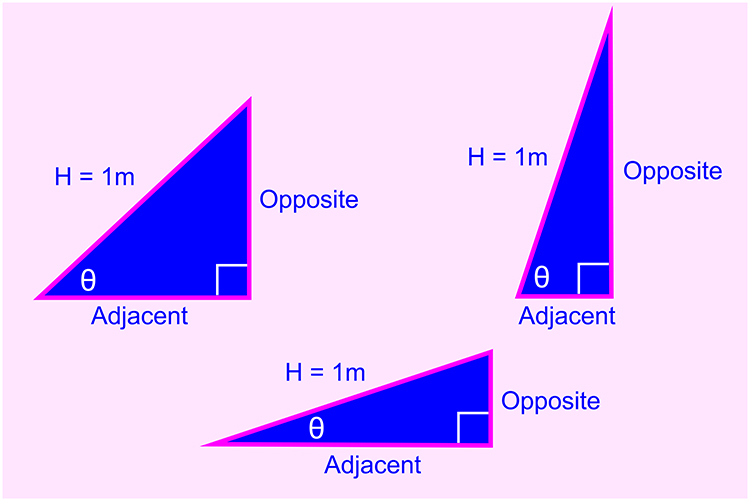
The mathematicians lifted a 1 metre stick up in one degree intervals and measured how far the end lifted off the floor

The mathematicians lifted a 1metre stick up in one degree intervals and measured how far the end lifted off the floor, and the adjacent length along the floor.

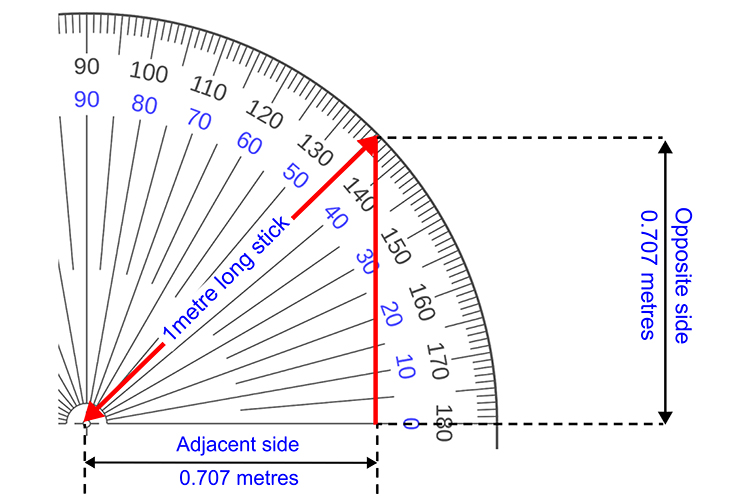
Fore each degree they measured the opposite side which changed slowly

And for each degree they measured the length of both the opposite and the adjacent side of the triangle and plotted it on a graph. (The red triangle above shows the stick at 45 degrees. The adjacent side is 0.707 metres along the floor.)

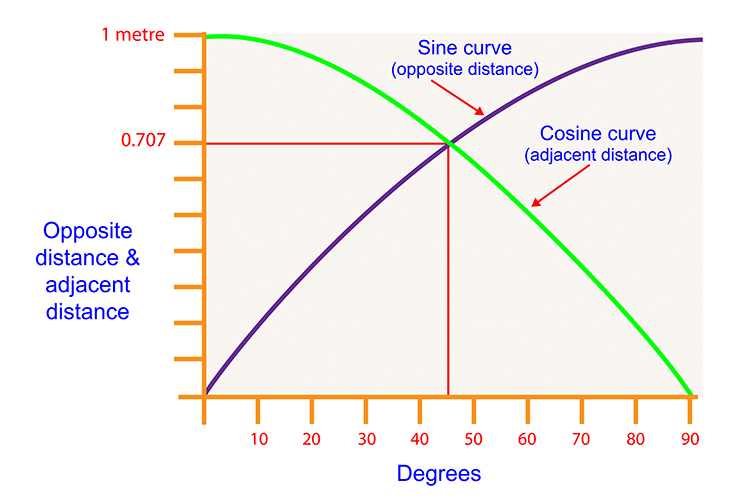
Both measurements were plotted on a graph this graph was called the TAN graph

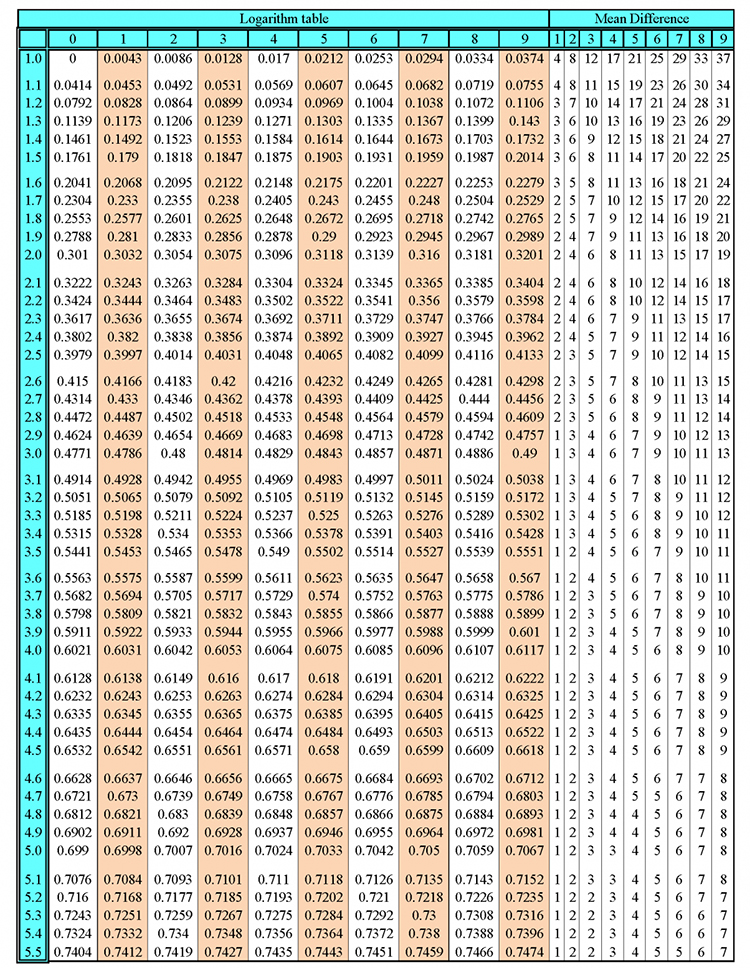
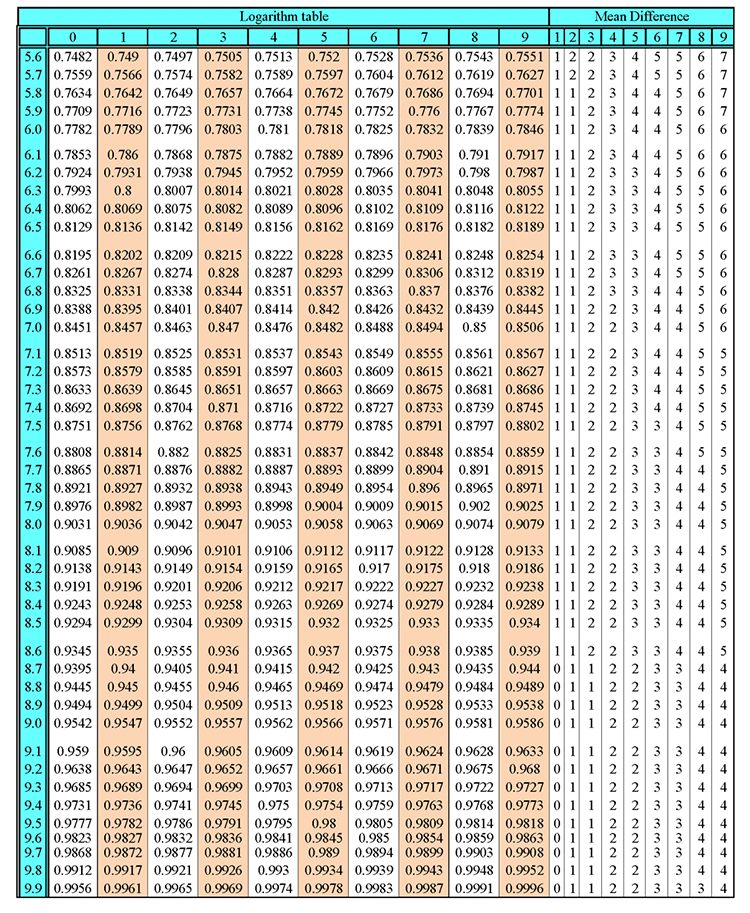
They then divided the opposite distance by the adjacent distance and they called that the table/chart of tan (angle). It reads as follows:

Angle	Opposite distance (or sine)	Adjacent distance (or cosine)	$(Opposite\ dist\ance\ (or sin))/(Adjacent\ dist\ance\ (or cos))$	= tan
$0^@$	$0 \ metres$	$1 \ metre$	$0/1$	$=0$
$1^@$	$0.01745 \ metres$	$0.99985 \ metres$	$0.01745/0.99985$	$=0.01746$
$2^@$	$0.03490 \ metres$	$0.99939 \ metres$	$0.03490/0.99939$	$=0.03492$
$3^@$	$0.05234 \ metres$	$0.99863 \ metres$	$0.05234/0.99863$	$=0.05241$
$4^@$	$0.06976 \ metres$	$0.99756 \ metres$	$0.06976/0.99756$	$=0.06993$
$5^@$	$0.08716 \ metres$	$0.99619 \ metres$	$0.08716/0.99619$	$=0.08749$
$6^@$	$0.10453 \ metres$	$0.99452 \ metres$	$0.10453/0.99452$	$=0.10510$
$7^@$	$0.12187 \ metres$	$0.99255 \ metres$	$0.12187/0.99255$	$=0.12278$
$8^@$	$0.13917 \ metres$	$0.99027 \ metres$	$0.13917/0.99027$	$=0.14054$
$9^@$	$0.15643 \ metres$	$0.98769 \ metres$	$0.15643/0.98769$	$=0.15838$
$10^@$	$0.17365 \ metres$	$0.98481 \ metres$	$0.17365/0.98163$	$=0.17633$
$11^@$	$0.19081 \ metres$	$0.98163 \ metres$	$0.19081/0.98163$	$=0.19438$
$12^@$	$0.20791 \ metres$	$0.97815 \ metres$	$0.20791/0.97815$	$=0.21256$
$13^@$	$0.22495 \ metres$	$0.97437 \ metres$	$0.22495/0.97437$	$=0.23087$
$14^@$	$0.24192 \ metres$	$0.97030 \ metres$	$0.24192/0.97030$	$=0.24933$
$15^@$	$0.25882 \ metres$	$0.96593 \ metres$	$0.25882/0.96593$	$=0.26795$
$16^@$	$0.27564 \ metres$	$0.96126 \ metres$	$0.27564/0.96126$	$=0.28675$
$17^@$	$0.29237 \ metres$	$0.95630 \ metres$	$0.29237/0.95630$	$=0.30573$
$18^@$	$0.30902 \ metres$	$0.95106 \ metres$	$0.30902/0.95106$	$=0.32492$
$19^@$	$0.32557 \ metres$	$0.94552 \ metres$	$0.32557/0.94552$	$=0.34433$
$20^@$	$0.34202 \ metres$	$0.93969 \ metres$	$0.34202/0.93969$	$=0.36397$
$21^@$	$0.35837 \ metres$	$0.93358 \ metres$	$0.35837/0.93358$	$=0.38386$
$22^@$	$0.37461 \ metres$	$0.92718 \ metres$	$0.37461/0.92718$	$=0.40403$
$23^@$	$0.39073 \ metres$	$0.92050 \ metres$	$0.39073/0.92050$	$=0.42447$
$24^@$	$0.40674 \ metres$	$0.91355 \ metres$	$0.40674/0.91355$	$=0.44523$
$25^@$	$0.42262 \ metres$	$0.90631 \ metres$	$0.42262/0.90631$	$=0.46631$
$26^@$	$0.43837 \ metres$	$0.89879 \ metres$	$0.43837/0.89879$	$=0.48773$
$27^@$	$0.45399 \ metres$	$0.89101 \ metres$	$0.45399/0.89101$	$=0.50952$
$28^@$	$0.46947 \ metres$	$0.88295 \ metres$	$0.46947/0.88295$	$=0.53171$
$29^@$	$0.48481 \ metres$	$0.87462 \ metres$	$0.48481/0.87462$	$=0.55431$
$30^@$	$0.5 \ metres$	$0.86603 \ metres$	$0.5/0.86603$	$=0.57735$
$31^@$	$0.51504 \ metres$	$0.85717 \ metres$	$0.51504/0.85717$	$=0.60086$
$32^@$	$0.52992 \ metres$	$0.84805 \ metres$	$0.54464/0.84805$	$=0.62487$
$33^@$	$0.54464 \ metres$	$0.83867 \ metres$	$0.54464/0.83867$	$=0.64941$
$34^@$	$0.55919 \ metres$	$0.82904 \ metres$	$0.55919/0.82904$	$=0.67451$
$35^@$	$0.57358 \ metres$	$0.81915 \ metres$	$0.57358/0.81915$	$=0.70021$
$36^@$	$0.58779 \ metres$	$0.80901 \ metres$	$0.58779/0.80901$	$=0.72654$
$37^@$	$0.60182 \ metres$	$0.79864 \ metres$	$0.60182/0.79864$	$=0.75355$
$38^@$	$0.61566 \ metres$	$0.78801 \ metres$	$0.61566/0.78801$	$=0.78128$
$39^@$	$0.62932 \ metres$	$0.77715 \ metres$	$0.62932/0.77715$	$=0.80978$
$40^@$	$0.64279 \ metres$	$0.76604 \ metres$	$0.64279/0.76604$	$=0.83910$
$41^@$	$0.65606 \ metres$	$0.75471 \ metres$	$0.65606/0.75471$	$=0.86928$
$42^@$	$0.66913 \ metres$	$0.74314 \ metres$	$0.66913/0.74314$	$=0.90040$
$43^@$	$0.68200 \ metres$	$0.73135 \ metres$	$0.68200/0.73135$	$=0.93251$
$44^@$	$0.69466 \ metres$	$0.71934 \ metres$	$0.69466/0.71934$	$=0.96569$
$45^@$	$0.70711 \ metres$	$0.70711 \ metres$	$0.70711/0.70711$	$=1$
$46^@$	$0.71934 \ metres$	$0.69466 \ metres$	$0.71934/0.69466$	$=1.03553$
$47^@$	$0.73135 \ metres$	$0.68200 \ metres$	$0.73135/0.68200$	$=1.07237$
$48^@$	$0.74314 \ metres$	$0.66913 \ metres$	$0.74314/0.66913$	$=1.11061$
$49^@$	$0.75471 \ metres$	$0.65606 \ metres$	$0.75471/0.65606$	$=1.15037$
$50^@$	$0.76604 \ metres$	$0.64279 \ metres$	$0.76604/0.64279$	$=1.19175$
$51^@$	$0.77715 \ metres$	$0.62932 \ metres$	$0.77715/0.62932$	$=1.23490$
$52^@$	$0.78801 \ metres$	$0.61566 \ metres$	$0.78801/0.61566$	$=1.27994$
$53^@$	$0.79864 \ metres$	$0.60182 \ metres$	$0.79864/0.60182$	$=1.32704$
$54^@$	$0.80901 \ metres$	$0.58779 \ metres$	$0.80901/0.58779$	$=1.37638$
$55^@$	$0.81915 \ metres$	$0.57358 \ metres$	$0.8195/0.57358$	$=1.42815$
$56^@$	$0.82904 \ metres$	$0.55919 \ metres$	$0.82904/0.55919$	$=1.48256$
$57^@$	$0.83867 \ metres$	$0.54464 \ metres$	$0.83867/0.54464$	$=1.53986$
$58^@$	$0.84805 \ metres$	$0.52992 \ metres$	$0.84805/0.52992$	$=1.60033$
$59^@$	$0.85717 \ metres$	$0.51504 \ metres$	$0.85717/0.51504$	$=1.66428$
$60^@$	$0.86603 \ metres$	$0.5 \ metres$	$0.86603/0.5$	$=1.73205$
$61^@$	$0.87462 \ metres$	$0.48481 \ metres$	$0.087462/0.48481$	$=1.80405$
$62^@$	$0.88295 \ metres$	$0.46947 \ metres$	$0.88295/0.46947$	$=1.88073$
$63^@$	$0.89101 \ metres$	$0.45399 \ metres$	$0.89101/0.45399$	$=1.96261$
$64^@$	$0.89879 \ metres$	$0.43837 \ metres$	$0.89879/0.43837$	$=2.05030$
$65^@$	$0.90631 \ metres$	$0.42262 \ metres$	$0.90631/0.42262$	$=2.14450$
$66^@$	$0.91355 \ metres$	$0.40674 \ metres$	$0.91355/0.40674$	$=2.24604$
$67^@$	$0.92050 \ metres$	$0.39073 \ metres$	$0.92050/0.39073$	$=2.35585$
$68^@$	$0.92718 \ metres$	$0.37461 \ metres$	$0.92718/0.37461$	$=2.47509$
$69^@$	$0.93358 \ metres$	$0.35837 \ metres$	$0.93358/0.35837$	$=2.60509$
$70^@$	$0.93969 \ metres$	$0.34202 \ metres$	$0.93969/0.34202$	$=2.74747$
$71^@$	$0.94552 \ metres$	$0.32557 \ metres$	$0.94552/0.32557$	$=2.90421$
$72^@$	$0.95106 \ metres$	$0.30902 \ metres$	$0.95106/0.30902$	$=3.07768$
$73^@$	$0.95630 \ metres$	$0.29237 \ metres$	$0.95630/0.29237$	$=3.27085$
$74^@$	$0.96126 \ metres$	$0.27564 \ metres$	$0.96126/0.27564$	$=3.48741$
$75^@$	$0.96593 \ metres$	$0.25882 \ metres$	$0.96593/0.25882$	$=3.73205$
$76^@$	$0.97030 \ metres$	$0.24192 \ metres$	$0.97030/0.24192$	$=4.01078$
$77^@$	$0.97437 \ metres$	$0.22495 \ metres$	$0.97437/0.22495$	$=4.33148$
$78^@$	$0.97815 \ metres$	$0.20791 \ metres$	$0.97815/0.20791$	$=4.70463$
$79^@$	$0.98163 \ metres$	$0.19081 \ metres$	$0.98163/0.19081$	$=5.14455$
$80^@$	$0.98481 \ metres$	$0.17365 \ metres$	$0.98481/0.17365$	$=5.67128$
$81^@$	$0.98769 \ metres$	$0.15643 \ metres$	$0.98769/0.15643$	$=6.31375$
$82^@$	$0.99027 \ metres$	$0.13917 \ metres$	$0.99027/0.13917$	$=7.11537$
$83^@$	$0.99255 \ metres$	$0.12187 \ metres$	$0.99255/0.12187$	$=8.14435$
$84^@$	$0.99452 \ metres$	$0.10453 \ metres$	$0.99452/0.10453$	$=9.51436$
$85^@$	$0.99619 \ metres$	$0.08716 \ metres$	$0.99619/0.08716$	$=11.43005$
$86^@$	$0.99756 \ metres$	$0.06976 \ metres$	$0.99756/0.06976$	$=14.30067$
$87^@$	$0.99863 \ metres$	$0.05234 \ metres$	$0.99863/0.05234$	$=19.08114$
$88^@$	$0.99939 \ metres$	$0.03490 \ metres$	$0.99939/0.03490$	$=28.63625$
$89^@$	$0.99985 \ metres$	$0.01745 \ metres$	$0.99985/0.01745$	$=57.28996$
$90^@$	$1 \ metre$	$0 \ metres$	undefined	undefined

Example 1

If the adjacent of a right angle triangle is 2 metres long and the opposite side is 1 metre long, what is the angle $theta$ ?

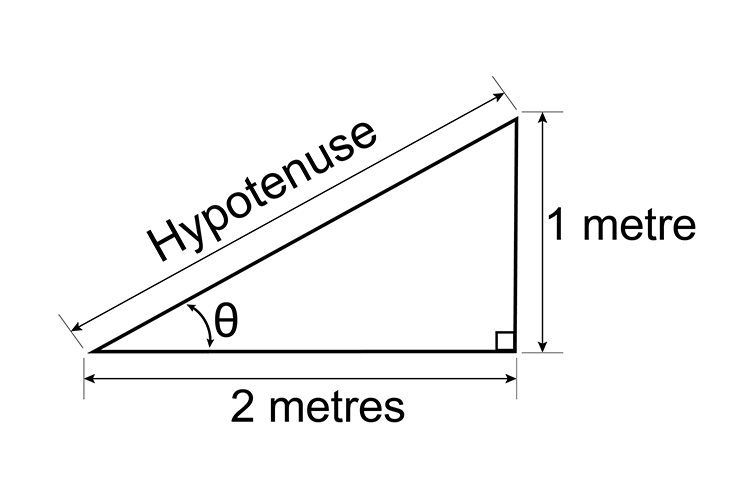
Measure the angle if the adjacent is 2 meters and the opposite side is 1 meter

Here we don’t know the hypotenuse, but we do know the length of the adjacent and opposite sides.

Simply divide the opposite by the adjacent length to calculate the unknown length.

i.e. $1/2=0.5$

Look up on the table/chart of tan (angle) for 0.5 metres above.

Angle	$(Opposite\ dist\ance\ (sin))/(Adjacent\ dist\ance\ (cos))$		= tan
Angle			= tan
?		0.5

The nearest = 27°

But on a calculator if you put in 0.5 and press inverse tan (tan^-1), this gives you 26.56°, which is more accurate.