Sine examples
Example 1
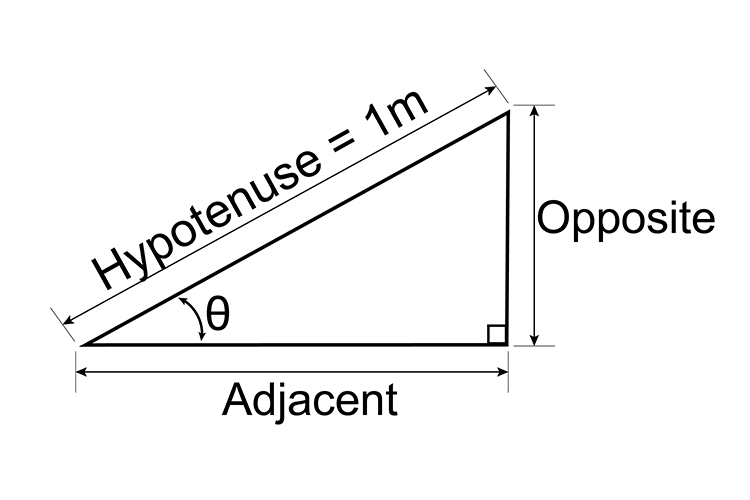
If the hypotenuse is 1 metre long and `theta=35^@`, how long is the opposite side?
Look up on the table/chart of sine (angle) for `35^@`or look up sine `35^@` on a calculator.
|
Angle |
Opposite distance (or sine) |
|
|
`35^@` |
`0.5736 metres` |
Answer:
Hypotenuse = 1 metre,
`theta=35^@`,
Therefore, Opposite = 0.5736 metres.
Example 2
If the hypotenuse is 1 metre long and `theta=45^@`, how long is the opposite side?
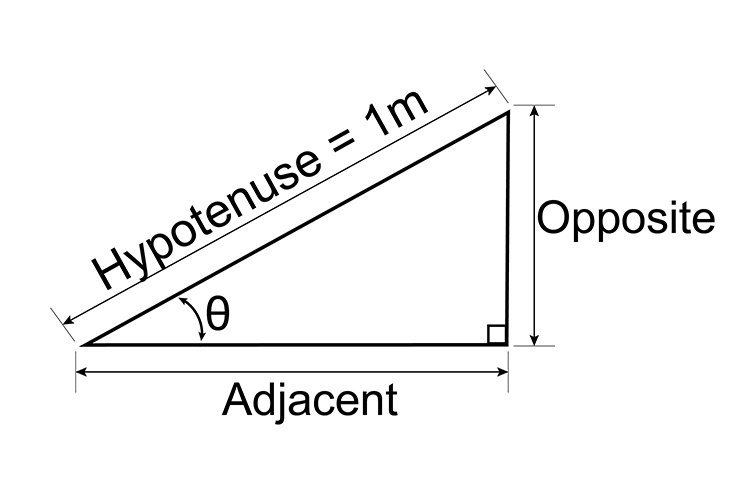
Look up on the table/chart of sine (angle) for `45^@` or look up sine `45^@` on a calculator.
|
Angle |
Opposite distance (or sine) |
|
|
`45^@` |
`0.7071 metres` |
Answer:
Hypotenuse = 1 metre,
`theta=45^@`,
Therefore, Opposite = 0.7071 metres.
Example 3
If the hypotenuse is 1 metre long, and the opposite side is 0.8 metres long, what is the angle `theta` ?

Look up on the table/chart of sine (angle) for 0.8 metres and find the angle.
|
Angle |
Opposite distance (or sine) |
|
|
? |
`0.8 metres` |
The nearest = 54° = 0.809 metres.
But on a calculator if you put in 0.8 and press inverse sin (sin-1), this gives you 53.13° (which is more accurate).
Example 4
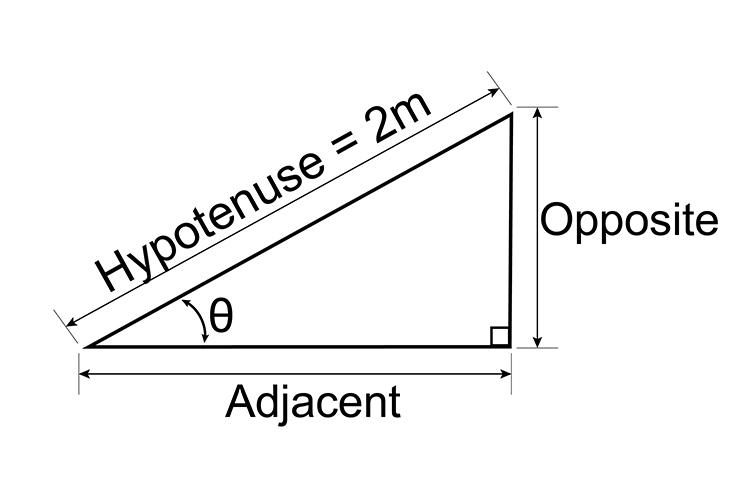
If the hypotenuse is 2 metres long and `theta=45^@`, how long is the opposite side?
Look up on the table/chart of sine (angle) for `45^@` or look up sine `45^@` on a calculator.
|
Angle |
Opposite distance (or sine) |
|
|
`45^@` |
`0.7071 metres` |
But 0.7071 is for a 1m hypotenuse.
For a hypotenuse of 2m, the opposite would be twice as long.
Therefore `0.7071times2=1.4142`
Answer:
Hypotenuse = 2 metres,
`theta=45^@`,
Therefore opposite = 1.4142 metres.




