The sine curve and cosine curve
You really don’t need to know this but again it could provide background help to some.
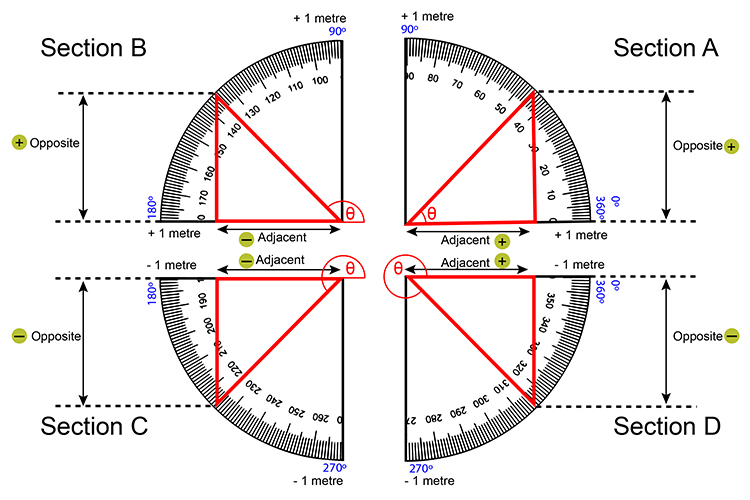
Following on from using a 1m stick to find the relationship between adjacent and cosine and the opposite and sine, the mathematicians took this 1m long hypotenuse triangle and continued to move the hypotenuse around in a circle, still taking measurements of the opposite lengths (sine) and the adjacent (cosine).
Pictorially this is what happened.
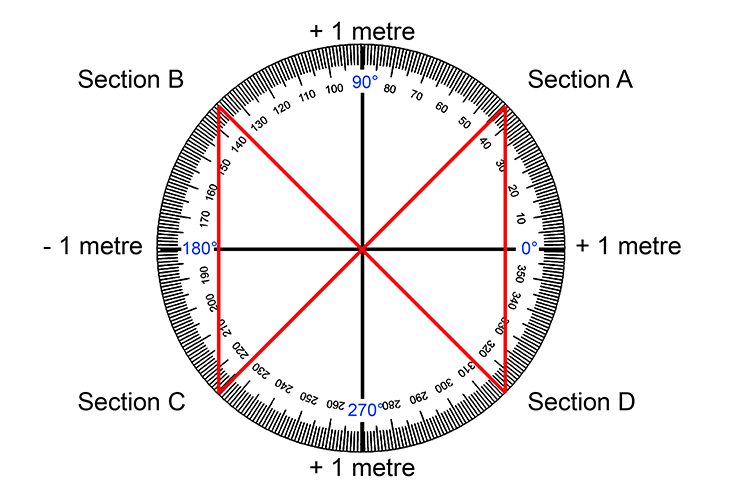
The red triangles just show the position of the 1 metre stick at 45°, 135°, 225° and 315°.