Practical examples of trigonometry

Example 1

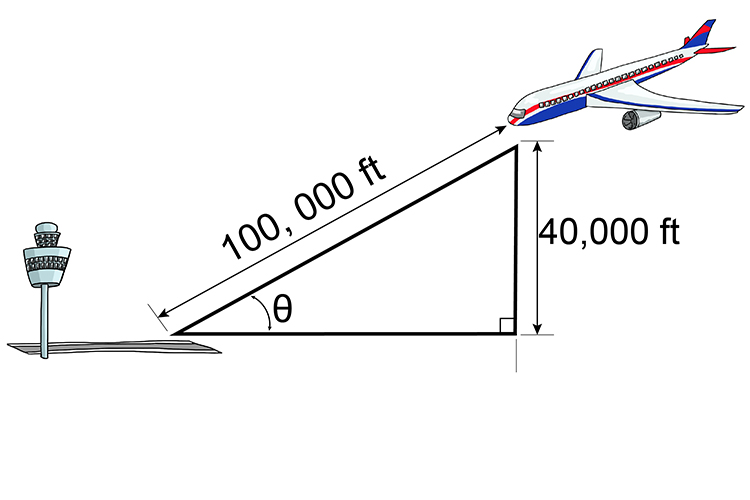
An air traffic controller is told by a pilot that she wants to land. She is currently at 40,000ft and wants to know what angle of descent to take. The air traffic controller can see on the radar that her plane is 100,000ft away from the runway.

NOTE:

The radar only measures directly to the plane and back, therefore the 100,000ft is the hypotenuse.

Measure the decent of a landing aircraft using trigonometry

Start by writing down the name of the great trigger-happy Indian war chief.

SOH CAH TOA

Work out which part of the triangle is which:

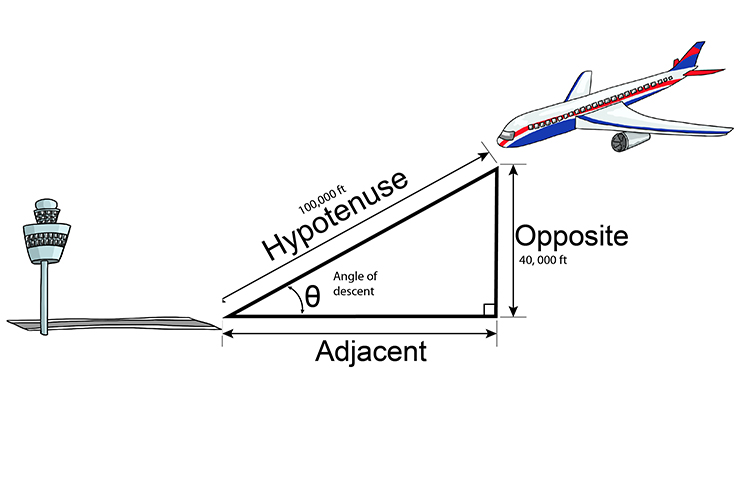
Example 1 work out which part of the triangle is which using sin cos tan

Looking at the diagram, we need `theta` (the angle of descent) and we know the lengths of the hypotenuse and the opposite. The only formula with hypotenuse, `theta` and opposite in it is:

`sin\ theta= (O)/(H)`

Or `sin\ theta= (Opposite)/(Hypoten\use)`

`sin\ theta= (40,000)/(100,000)`

`sin\ theta= 0.4`

Put 0.4 in your calculator and then press inverse sin or (sin^-1). This gives = 23.6

Answer:

The pilot must descend at an angle of 23.6°

Example 2

A home owner is worried that a particular tree could fall onto her house. The house is 80 feet away, but she is not sure how tall the tree is. She asks the schoolkid next door to work it out for her.

Work out the height of the tree using its shadow

The kid measured the shadow length from the tree. She also had a large protractor and measured the angle as 50°.

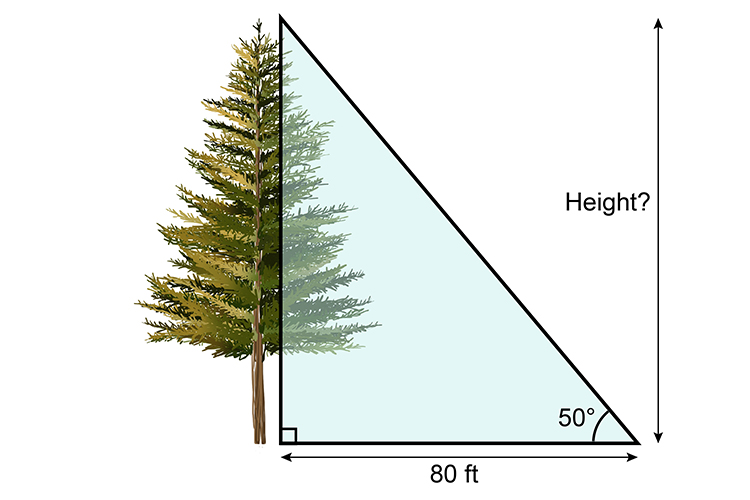
Work out the angle of the hypotenuse and adjacent sides of the triangle in this case it is 50 degrees

Then she did the following calculation:

She started by writing down the name of the great trigger-happy Indian war chief.

SOH CAH TOA

She worked out which part of the triangle she needed:

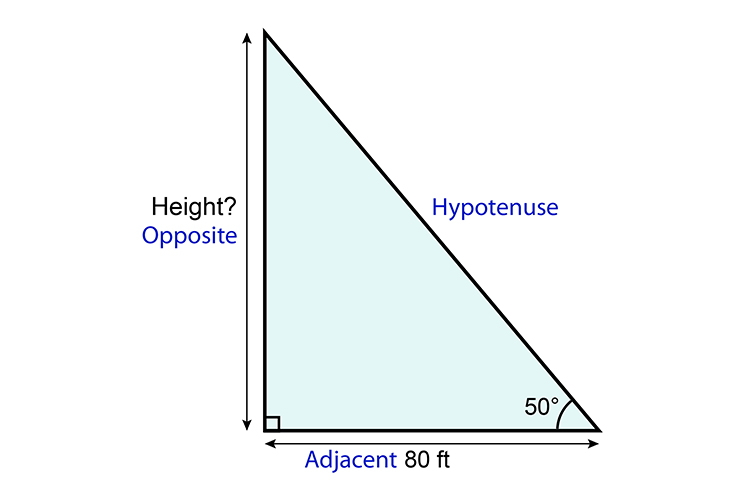
Work out which sides of the triangle you need to complete the task

She needed opposite and adjacent.

So she chooses `tan\ theta= (O)/(A)`

Or `tan\ theta= (Opposite)/(Adjacent)`

`tan\ 50= (O)/(A)`

`tan\ 50= (Opposite\ (height))/80`

`Opposite\ (height)=tan\ 50times80`

(To find `tan\ 50` put 50 into your calculator and then press the tan button. You should get 1.1918)

`Opposite\ (height)=1.1918times80`

`Height=95.3\ feet`

Answer:

Yes, the house is in danger of being hit if the tree falls over.

Example 3

You have to build a ramp into a building, but it must be no more than a 5° angle, as required by building regulations. If the height of the door above the ground is 400mm, how long should the ramp be?

Measure how long a ramp has to be is the angle needs to stay at 5 degrees

Start by writing down the name of the great trigger-happy Indian war chief.

SOH CAH TOA

Work out which part of the triangle is which:

Choose which sides of the triangle are necessary to complete the calculation

So we choose opposite and hypotenuse.

Choose `sin\ theta= (O)/(H)`

Or `sin\ theta= (Opposite)/(Hypoten\use)`

Or `sin\ 5= (400mm)/(Hypoten\use)`

Rearrange the formula

`Hypoten\use=(400mm)/sin5`

On a calculator press 5 and then sin and you get 0.08716.

`Hypoten\use=(400mm)/0.08716`

`Hypoten\use=4589mm\ \ or\ \ 4.6m` (to the nearest 0.1m)

Answer:

The ramp has to be 4.6m long.