And/Or

You don’t need to worry about the word definitions of AND/OR if you draw a probability diagram

Example AND

What is the probability of rolling a 6 on a dice AND getting heads on the toss of a coin?

`Probability\=(Right)/(All) =(The\ \n\umber\ of\ ways\ of \ ac\hiev\i\ng\ suc\c\ess)/(T\he\ \t\otal\ n\umber\ of \ possibl\e\ outcomes`

And

Always draw a probability tree.

`Rolli\ng\ a\ 6\ on\ a\ dice,probability=1/6\ \overset{(Right)}{\underset{(All\ possibl\e)}{text}} ]`

`Probability\ of\ heads\ on\ a\ coi\n=1/2\ \overset{(Right)}{\underset{(All\ possibl\e)}{text}} ]`

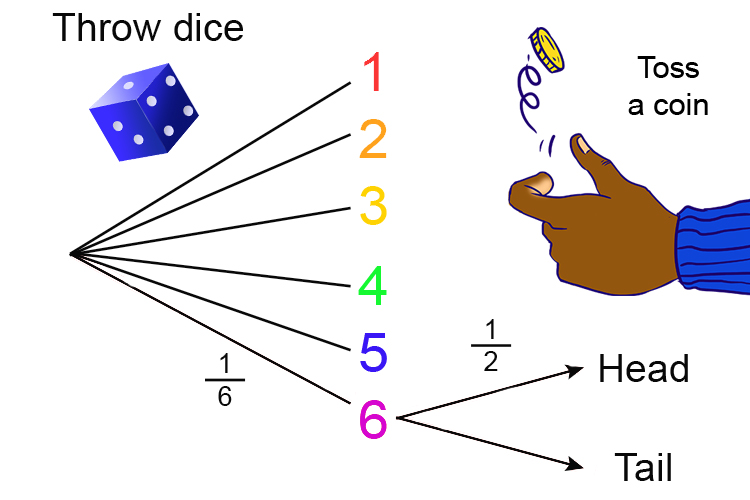
The probability of getting 6 on a dice and heads on a coin is 1 in 12

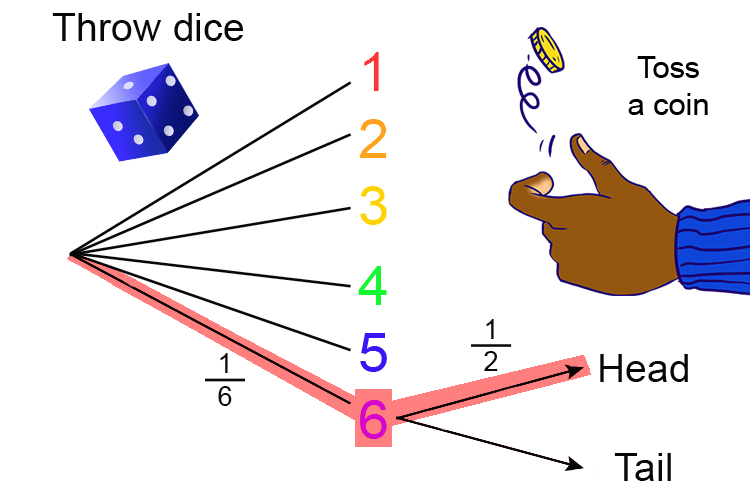
Dice probability is the same 1 in 6 and so is the coin 1 in 2, so just multiply the bigger numbers together

6 and heads = `1/6\times\1/2=1/12`

So AND = Multiply

If you draw a probability tree diagram you can see that the word 'and' in the question means that you should multiply the two probabilities.

Example Or

What is the probability of getting a 6 OR a 5 on the roll of a dice?

First remember

`Probability\=(Right)/(All) =(The\ \n\umber\ of\ ways\ of \ ac\hiev\i\ng\ suc\c\ess)/(T\he\ \t\otal\ n\umber\ of \ possibl\e\ outcomes`

And then

Always draw a probability tree.

`Rolli\ng\ a\ 6\ on\ a\ dice,probability=1/6\ \overset{(Right)}{\underset{(All\ possibilites)}{text}} ]`

`Rolli\ng\ a\ 5\ on\ a\ dice,probability=1/6\ \overset{(Right)}{\underset{(All\ possibilites)}{text}} ]`

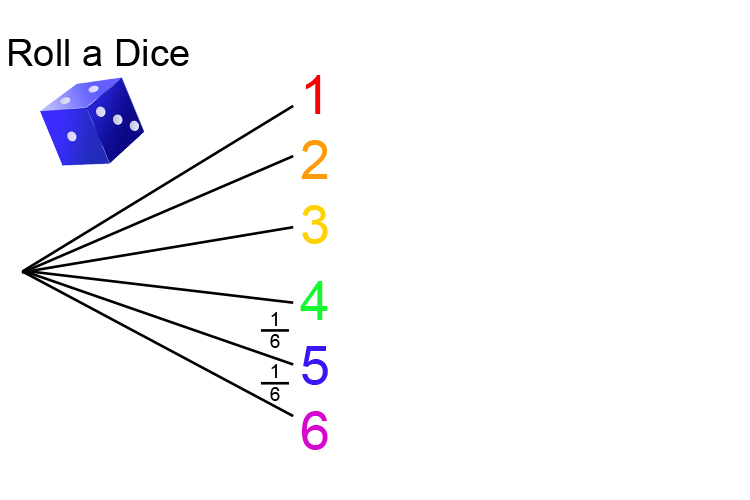
The probability of getting 5 and 6 on a dice is still 1 in 6

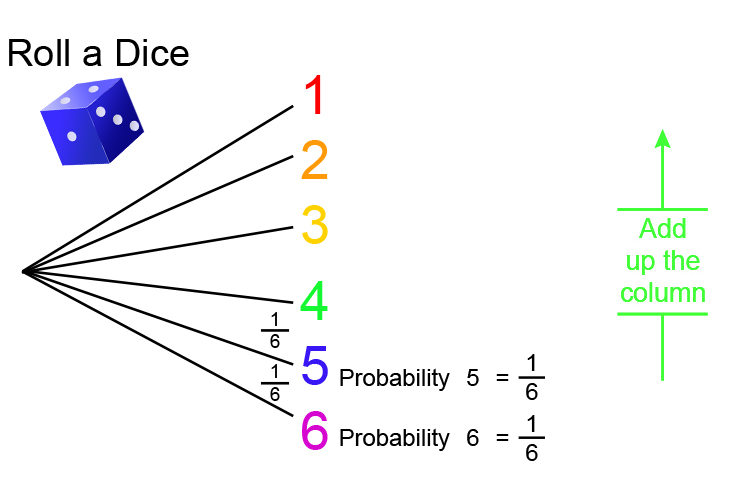
There are 2 throws so its 1 over 6 times 2 which is 1 in 3

`1/6+1/6=2/6=1/3`

So Or = Add

If you draw a probability tree diagram you can see that the word 'or' in the question means that you should add up the column.