Dice game of probability (Just for fun)

(This will never be in an exam but adds fun to maths and probability and teaches you the language and the strange nature of probability. Teachers should try this in class for fun)

Look at these unusual dice:

Look at these unusual dice, now see what's inside

We will open each up.

The first is:

What is in dice 1?

The second is:

What is in dice 2?

The third is:

What is in dice 3?

The fourth is:

What is in dice 4?

If we rank the dice as which is stronger, which is weaker by the definition:

"one die is stronger than the other die if that die has a higher probability of winning against the other die"

which means it wins more frequently.

Conversely

"One die is weaker than the other die if that die has a lower probability of winning against the other die."

Which means it loses more often.

Example 1

Which is the stronger dice?

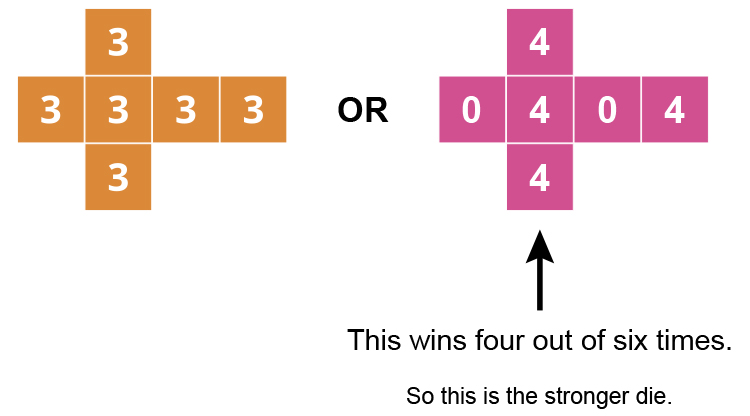
Which of these dice are stronger, the second wins its 4 out of 6 where the other is 3 out of 6

So the totem pole ranking would be:

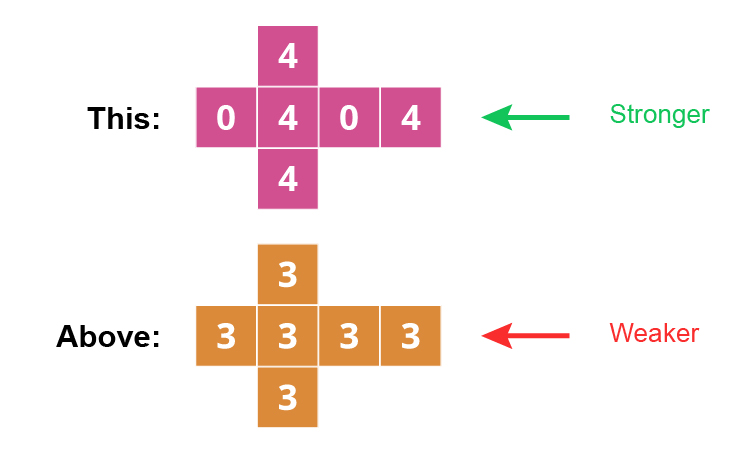
Dice 2 is stronger than dice 1

Example 2

Which is the stronger dice?

Dice 2 is stronger than dice 4

So the totem pole ranking would be:

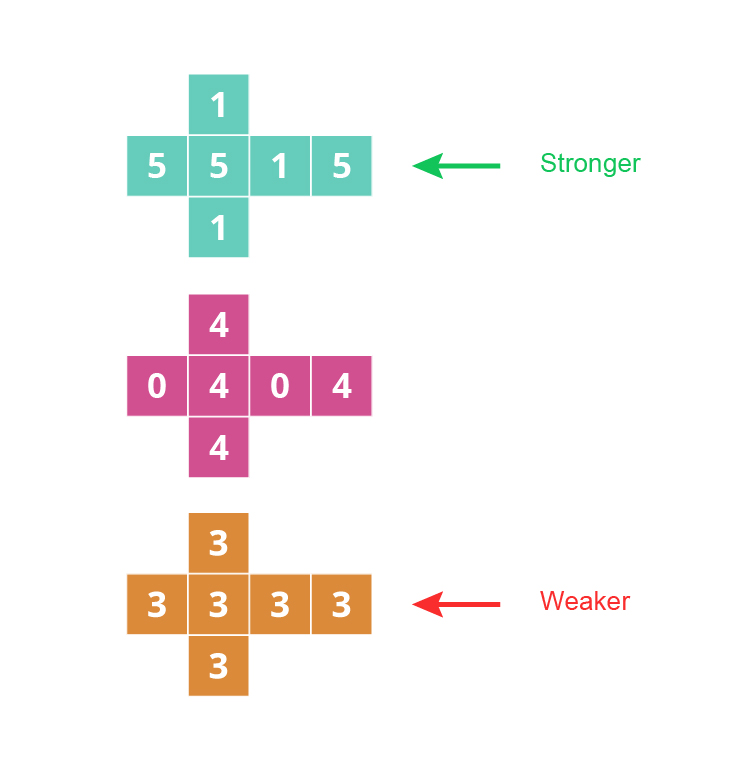
Dice 2 is stronger than 1 and 3

Example 3

Which is the stronger dice?

Which is stronger dice 3 or 5

Half the time this comes up `1` and if it did it
would lose every time against `6`, `6`, `2`, `2`, `2`, `2`

LOSE

Half the time this comes up `5` and if it did it
would lose twice against `6`, `6`, `2`, `2`, `2`, `2`

WIN

LOSE

WIN

LOSE

WIN

This loses 50% of the time `+` a bit more loss

So this is a weaker die

So the totem pole ranking would be:

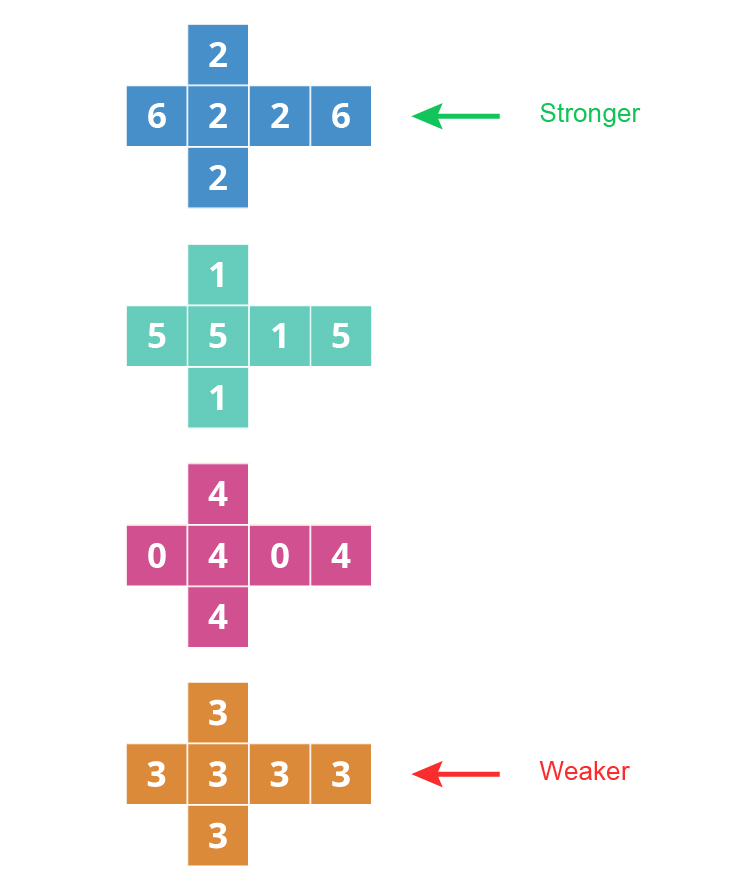
Dice 4 is the strongest in order down to 1

Example 4

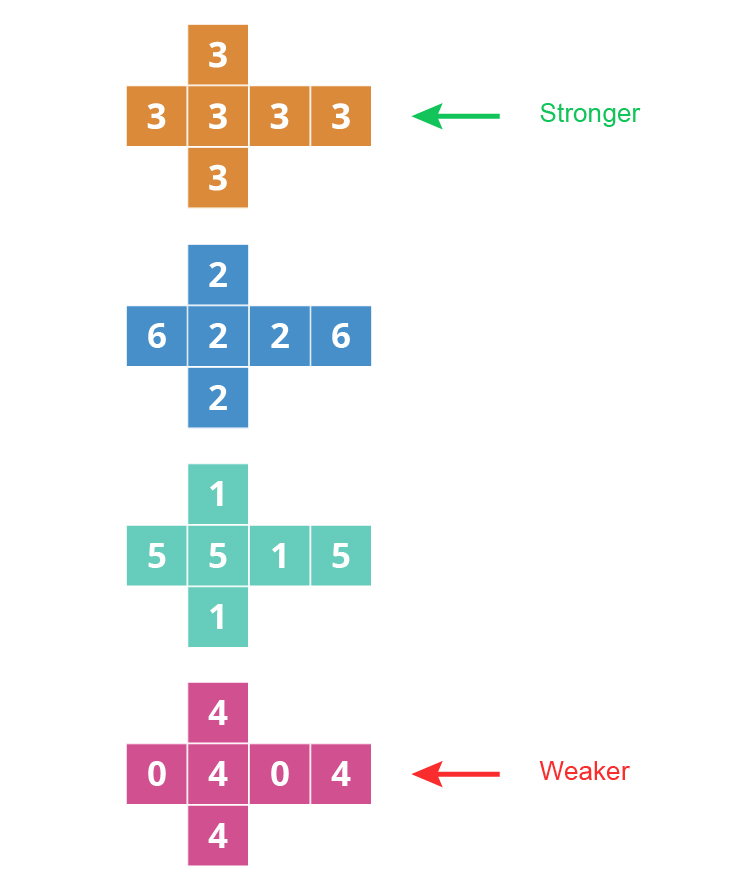
Now lets compare the two ends. Which is stronger?

Which is stronger 1 or 4

You would think this would be the `6`, `2`, `2`, `2`, `2`, `6` because of the above rankings but

`3`, `3`, `3`, `3`, `3`, `3` wins four out of six times. So this is the stronger die.

So the new totem pole ranking would be:

Dice 4 is the stronger than the rest

Example 5

If we do this again and compare the two ends we are comparing:

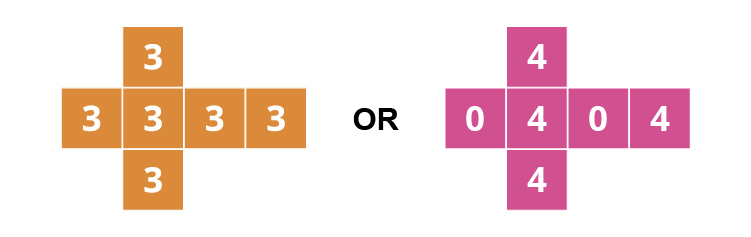
Compare dice 1 and 2

and we already know the answer (see example 1)

AND SO THE CYCLE CONTINUES

NOTES ABOUT THIS EXAMPLE

This cycle is called a non-transitive cycle in probabilistic comparisons.

This is important for people to know because if you compare `3` drugs:

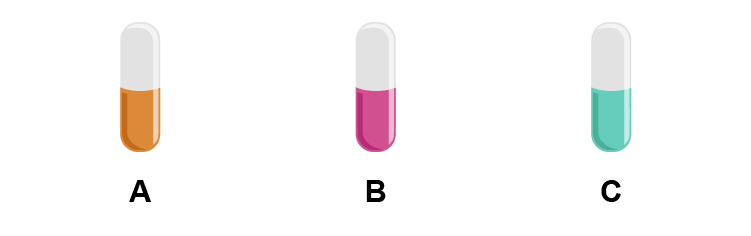
This cycle is called the non-transitive cycle

If A cures more people than B in one sample and B cures more people than C, you can not necessarily conclude that A is better than C. It might be true but not necessarily.