Independent Probability

Independent probability – one event DOES NOT affect the outcome of the other.

Independent probability event does not effect the outcome of the other

This woman is not dependent on anyone else to survive, she will never catch influenza (influence).

Independent probability - NOT Influenced

Example 1

A bag contains 6 marbles, four red and two yellow. A marble is taken from the bag, its colour written down then it is returned to the bag. A marble is again taken from the bag, and its colour written down.

1. What is the probability of getting two red marbles?

2. And what is the probability of getting a red and a yellow marble?

Start by drawing a probability tree:

In this example red has a 4 in 6 chance and yellow has a 2 in 6 chance of coming out

This can be redrawn as a probability tree

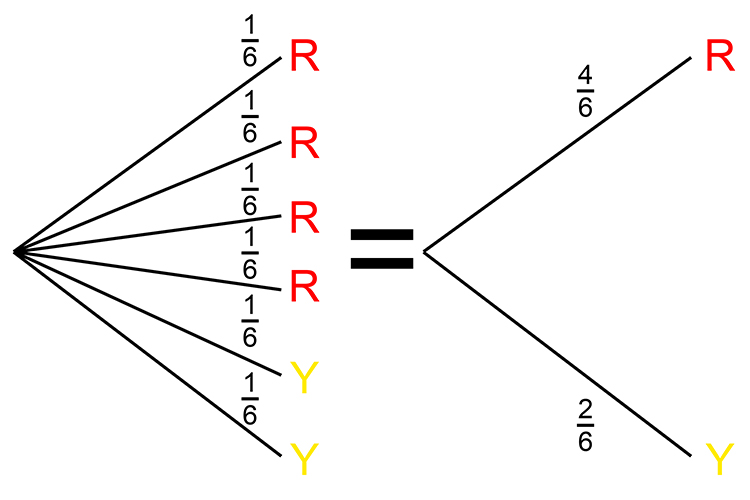
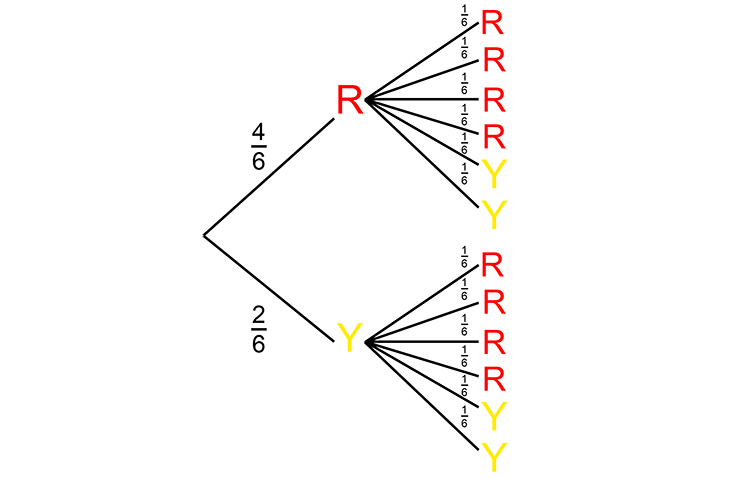
This can be redrawn as:

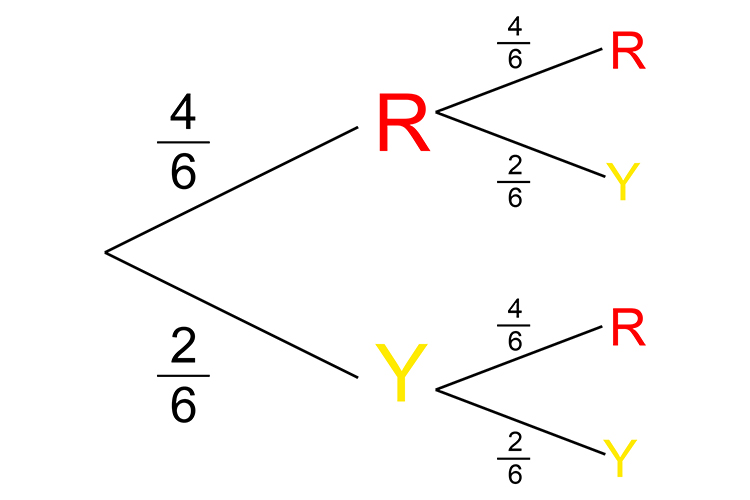
Another redraw

This is the probability tree for this example.

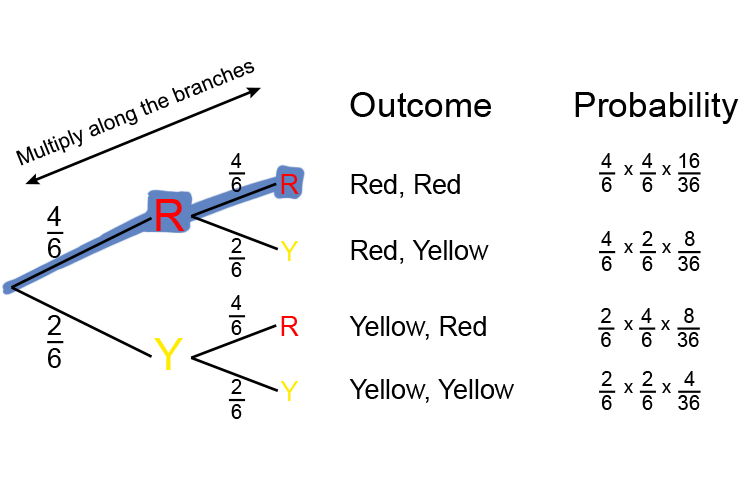
Probability of this example

Add these up to check they equal 1 $16/36+8/36+8/36+4/36=(16+8+8+4)/36=36/36=1$

I. Therefore from the diagram above the probability of getting two red marbles is:

Red, Red = $16/36=8/18=4/9$

Probability of two reds is 4 in 9 or = 0.44 And if 1 = 100% then 0.44 = 44% chance.

II. What is the probability of getting a red and a yellow marble?

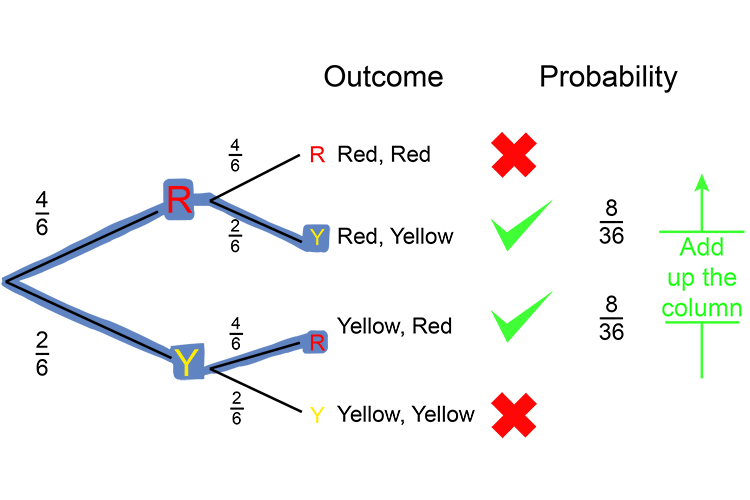
The probability of getting red and yellow marbles is 4 in 9

Add

$8/36+8/36=(8+8)/36=16/36=8/18=4/9$

The probability of getting a red and a yellow marble is 4 in 9 or = 0.44.

And if 1 = 100% then 0.44 = 44% chance.