Dependent Probability

Dependent probability – one event influences the outcome of the other (sometimes called conditional probability).

The baby is dependent on the mother. If the mum has influenza then the baby will get it too.

 Dependent probability - Influences 

Example 1

A bag contains 6 marbles, 4 red, and 2 yellow. A marble is taken from the bag and its colour is written down. The marble is not replaced, and another marble is taken out. What is the probability of getting two red marbles? And what is the probability of getting a red and a yellow marble?

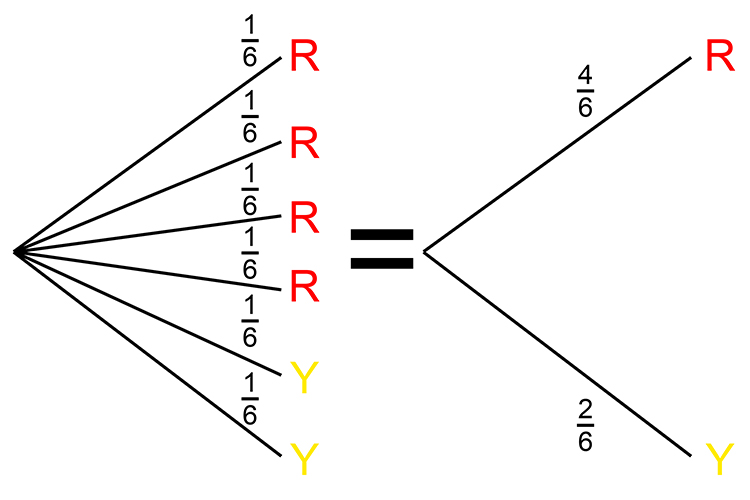
Start by drawing a probability tree:

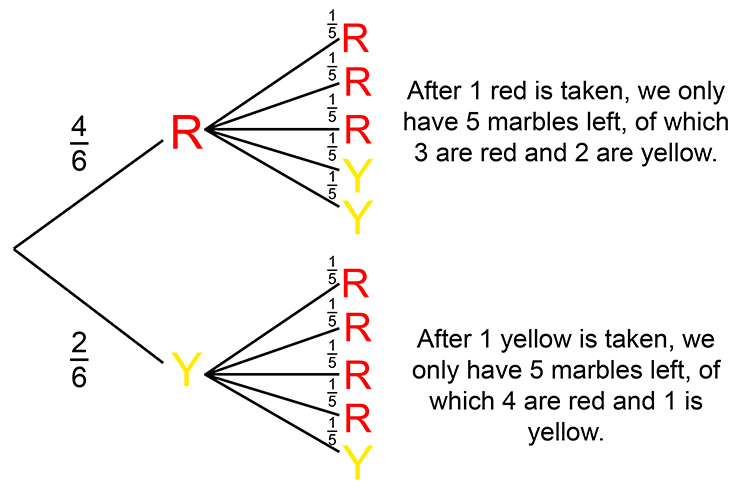
This can be redrawn as:

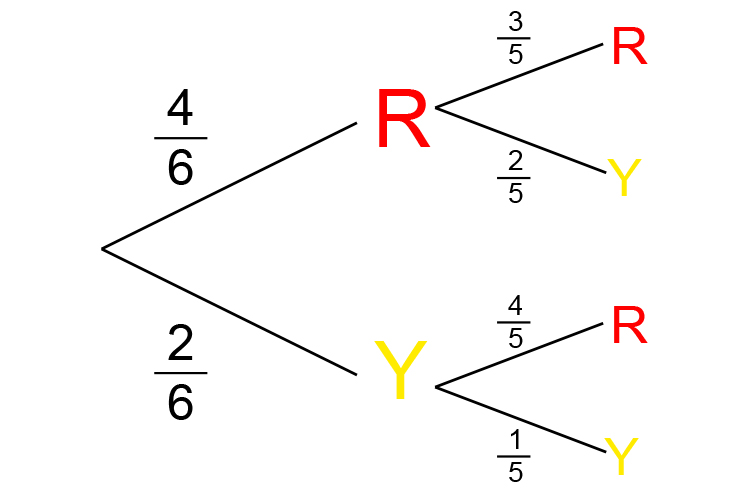
This is the probability tree for this example.

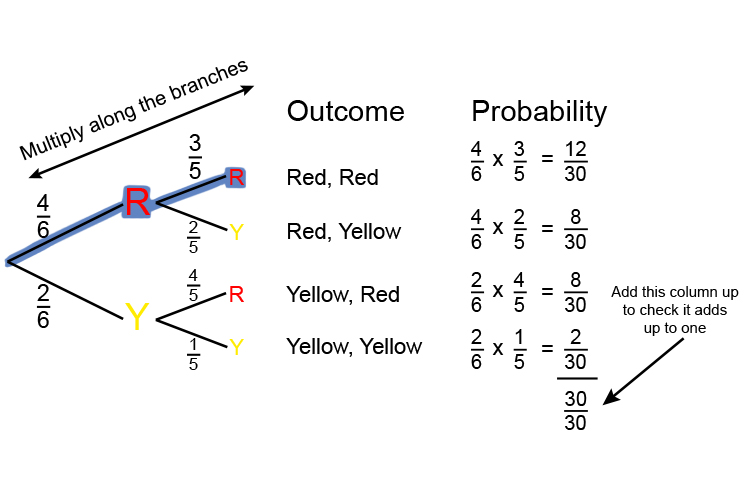
Therefore from the diagram above the probability of getting 2 red marbles is:

Red, Red = `12/30=6/15`

Probability of 2 reds is 6 in 15 or = 0.4 And if 1 = 100%   then 0.4 = 40% chance.

What is the probability of getting a red and a yellow marble (in any combination)?

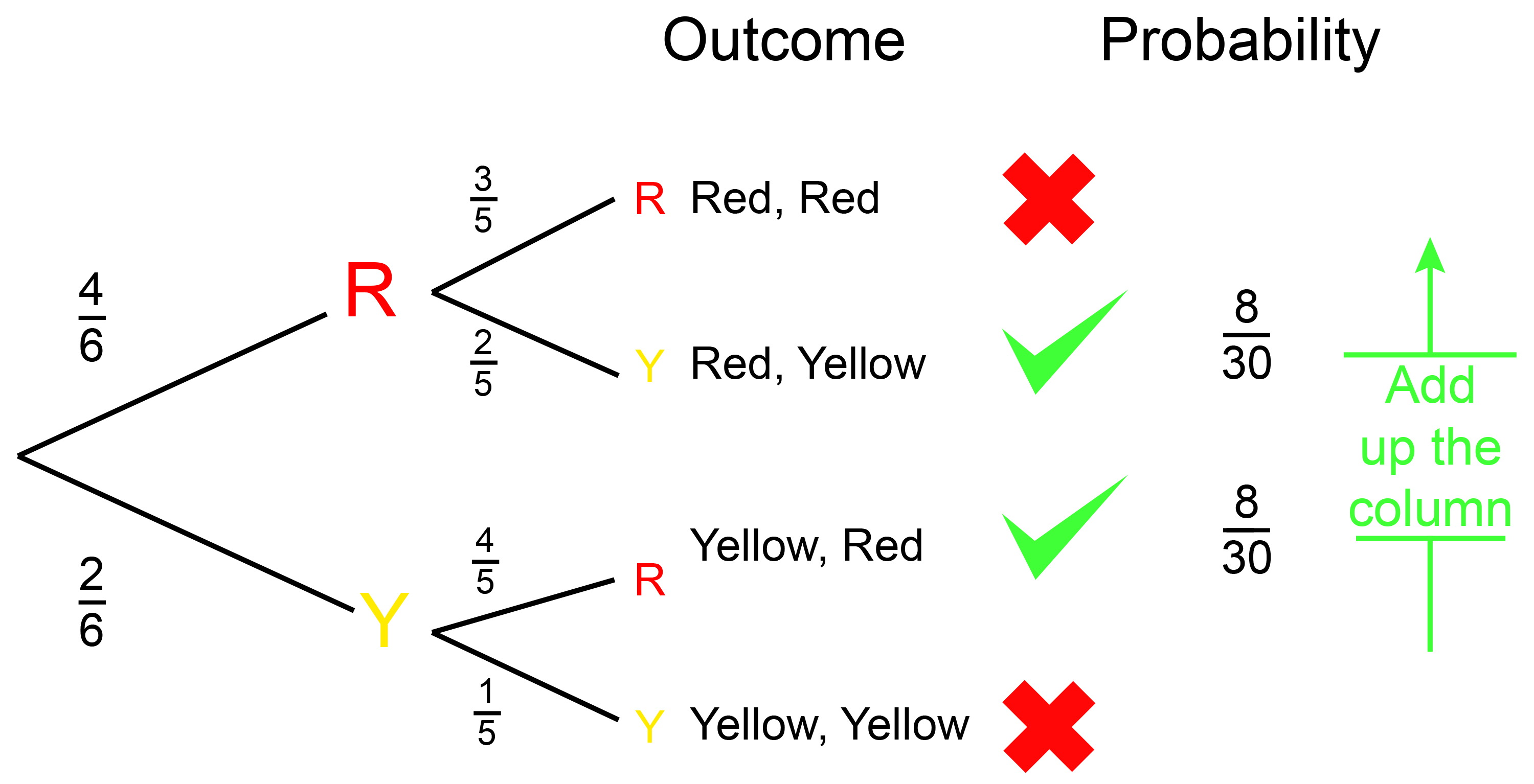
Add

`8/30+8/30=(8+8)/30=16/30=8/15`

The probability of a red and a yellow = 8 in 15 or = 0.53   And if 1 = 100%   then 0.53 = 53% chance.

Example 2

What is the probability of choosing 2 red cards from a deck of cards?

`Remember\ probability\ =(Number \ of\ RIGHT\ answers)/(Number\ of\ ALL\ possibl\e\ answers)`

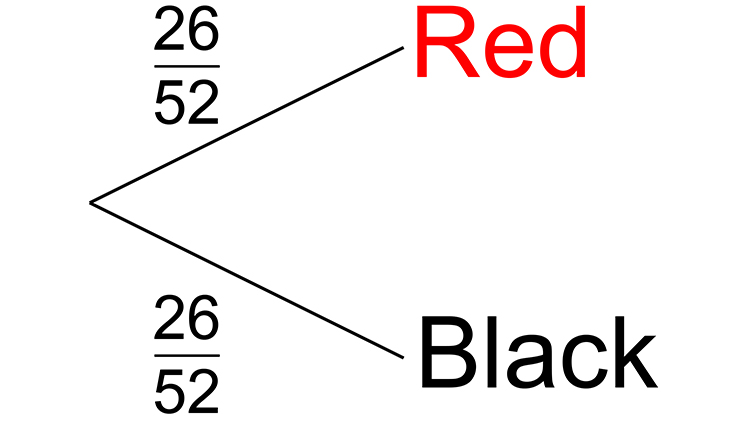
With 52 cards the chance of picking a red = `26/52`.

Start by drawing a probability tree:

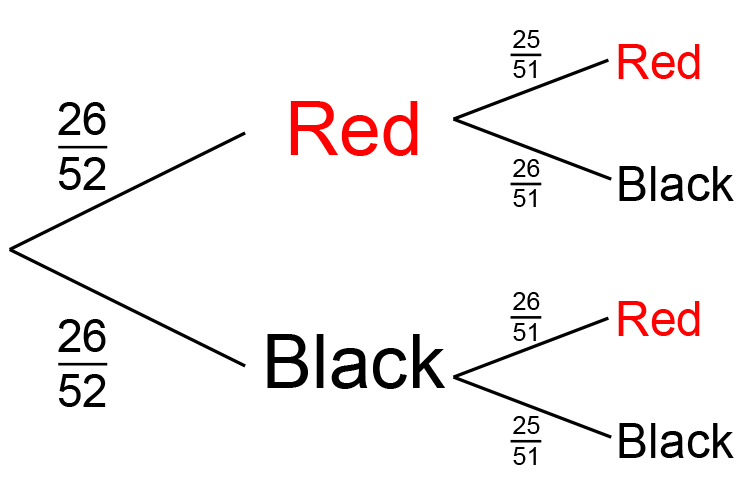
But now there are only 51 cards left to choose from if one red has already been taken.

The probability of another red = `25/51`.

Draw the probability tree now:

Multiply along the branches

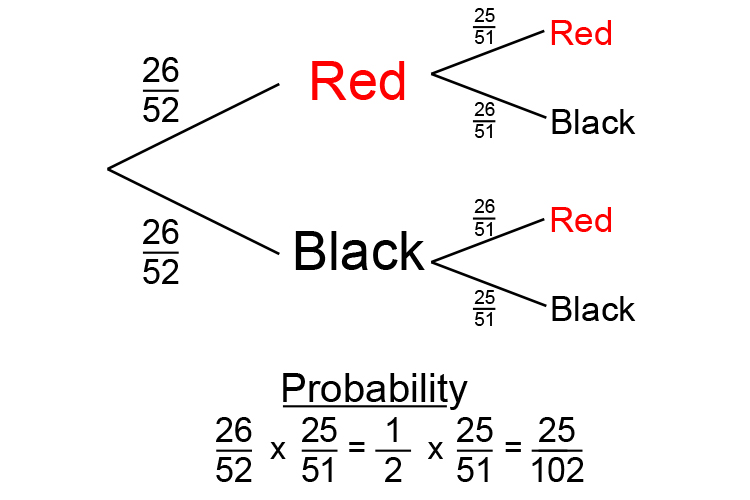
Answer: The probability of choosing two red cards from a deck of cards = 25 in 102 or 0.245.

And if 1 = 100%   then 0.245 = 24.5% chance.