How to remember the standard deviation

The standard deviation formula is:

Standard deviation `=sigma=sqrt((Sigma(x-bar x)^2)/(n-1))`

1. Find the mean (of all the numbers) `= barx`

2. Subtract the mean (from each number) `= x-barx`

3. Square the result (of each of the above) `= (x-barx)^2`

4. Add the results up (Add) `=sum(x-barx)^2`

5. Divide (the result) by the number of data values minus one `=(sum(x-barx)^2)/(n-1)`

6. Take the square root of the result `=sqrt((sum(x-barx)^2)/(n-1))`

The following story should help you remember all of the above.

Standard deviation `=sigma`

and these mean ones are taken out of the class `=x-barx`

`Each\ \n\u\m\b\er - mean`

they are all put in the school square `=s\q\u\a\r\e`

`(Each\ \n\u\m\b\er - mean)^2`

then there is a roll call to add up the deviants `=ADD`

`sum(Each\ \n\u\m\b\er - mean)^2`

then they have to run over ninety miles `=\ \/n`

`(sum(Each\ \n\u\m\b\er - mean)^2)/n`

there is always one that doesn't make it back `=-1`

`(sum(Each\ \n\u\m\b\er - mean)^2)/(n-1)`

This roots out any problems

`sqrt((sum(Each\ \n\u\m\b\er - mean)^2)/(n-1))`

So

Standard deviation `=sigma=sqrt((sum(x-barx)^2)/(n-1))`

In more detail and with pictures you would remember this as follows:

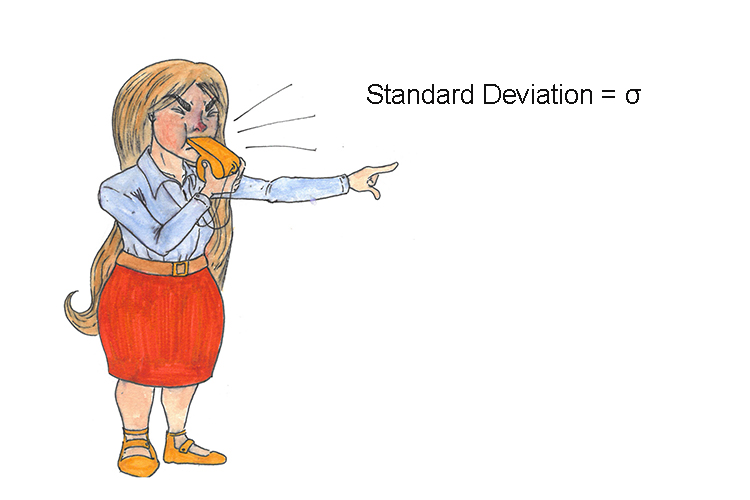
Mnemonic to help you remember the standard deviation symbol

To set the standards any deviants have a whistle blown at them.

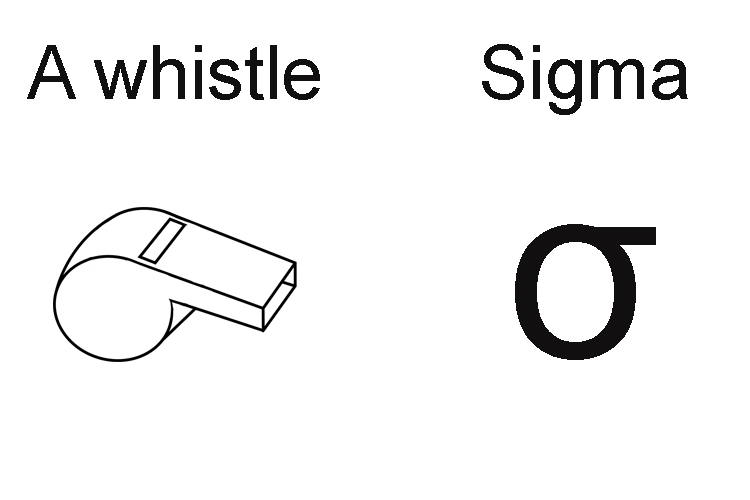
The sigma symbol looks like a whistle

A whistle and sigma look very alike.

Subtract the mean.

Then square each result.

Mnemonic to remember that you first need to subtract the mean

All these mean ones are then marched into the school square.

Add all the results.

Memory aid to help you remember to add the result

There is a roll call to add up all the deviants.

NOTE:

If you just learnt up to this point this would help you enormously with how to work out what the equation means.

Remember N

The deviants are made to run over (÷) ninety (n) miles.

Remember -1 so n-1

There is always one that doesn’t make it back (-1).

Square root the result.

Square root the result which will give you the answer

This roots out any problems (√).