Stratified sampling

A method of sampling a population where you

Divide into subcategories
Then samples taken from EVERY subcategory

1. Stratify (categorise) the population. “Strata” means “layer” and helps you remember that stratified means in layers or categories.

Stratified is dividing population into sub categories

The cats (categories) were all in stratified layers like a rock.

2. Sample every category

Sample from EVERY category

EACH cat had to be taken out to be saved.

For each category a sample is taken.

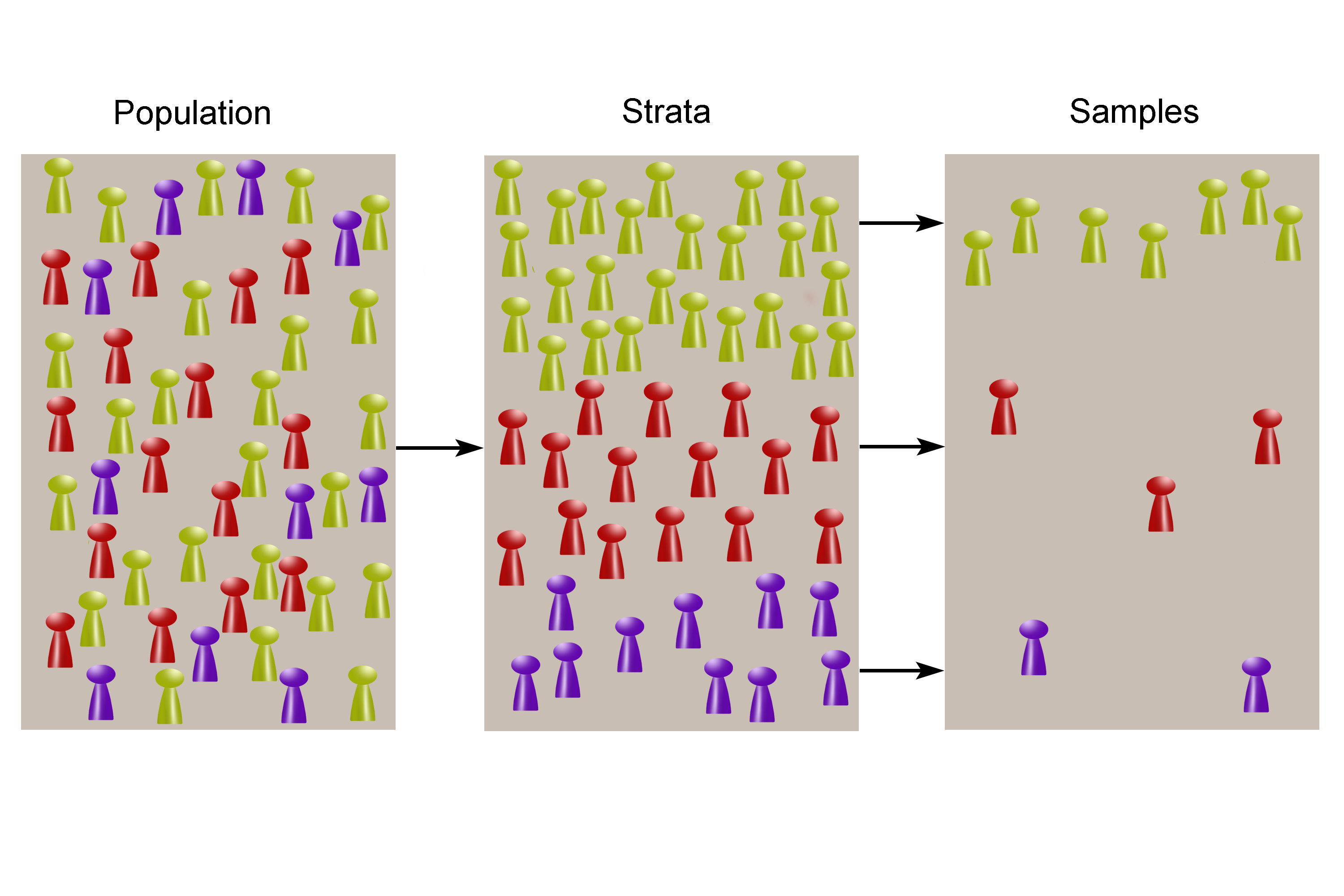
Ordering population by strata then sampling from every group created

A sample is taken from EACH category but in proportion to the size of each category.

Example 1

A school has 650 students. Each student studies one of Greek or Spanish or German or French. The table shows the number of students who study each of these languages.

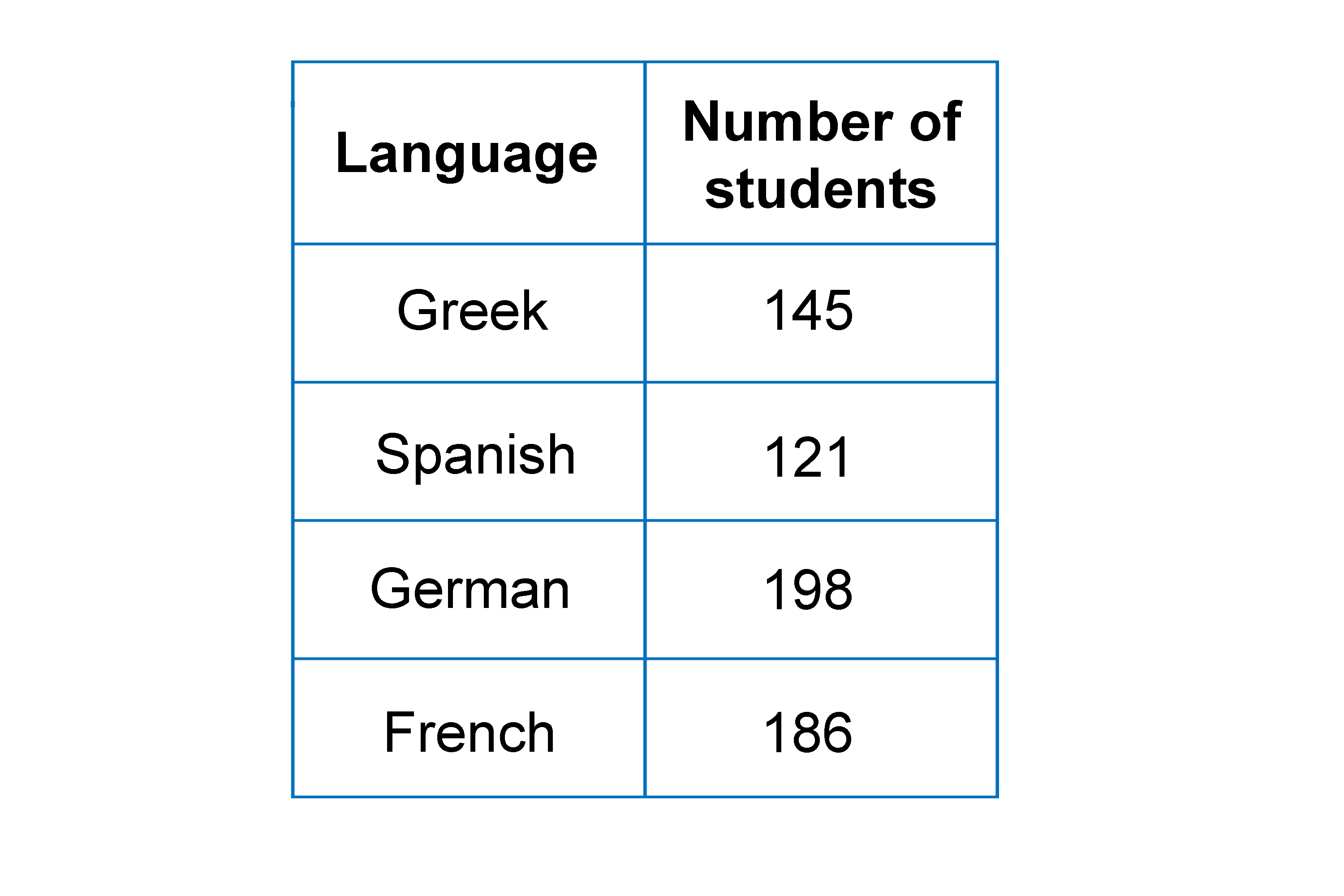
Inspect these samplings of students in this example

An inspector wants to look at the work of a stratified sample of 70 of these students.
Find the number of students studying each of these languages that should be in the sample.

Answer:

Greek:

If `650=100%`

`145=x%`

(see our section on percentages)

`650/145=100/x`

Therefore `x=(100times145)/650`

`x=22.3%`

And then

If `70=100%`

`x=22.3%`

`70/x=100/22.3`

Therefore `x=(70times22.3)/100`

`x=15.61`

The nearest whole number = 16

Spanish:

If `650=100%`

`121=x%`

(see our section on percentages)

`650/121=100/x`

Therefore `x=(100times121)/650`

`x=18.6%`

And then

If `70=100%`

`x=18.6%`

`70/x=100/18.6`

Therefore `x=(70times18.6)/100`

`x=13.02`

The nearest whole number = 13

German:

If `650=100%`

`198=x%`

(see our section on percentages)

`650/198=100/x`

Therefore `x=(100times198)/650`

`x=30.5%`

And then

If `70=100%`

`x=30.5%`

`70/x=100/30.5`

Therefore `x=(70times30.5)/100`

`x=21.35`

The nearest whole number = 21

French:

If `650=100%`

`186=x%`

(see our section on percentages)

`650/186=100/x`

Therefore `x=(100times186)/650`

`x=28.6%`

And then

If `70=100%`

`x=28.6%`

`70/x=100/28.6`

Therefore `x=(70times28.6)/100`

`x=20.02`

The nearest whole number = 20

Answer:

Greek sample size = 16

Spanish sample size = 13

German sample size = 21

French sample size = 20

Example 2

A school has the following number of pupils in each year group:

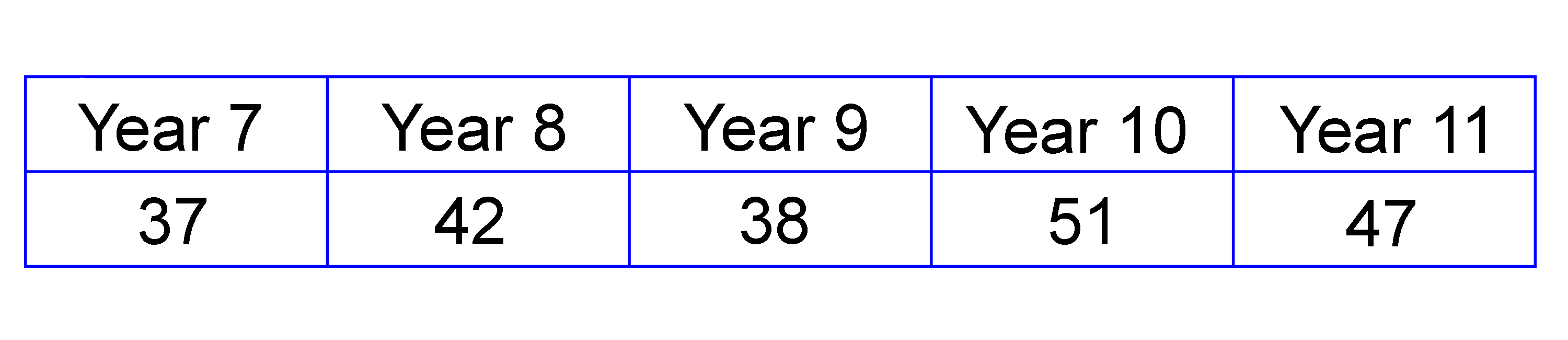
Stratified sampling example 2

The school wants to find out what after-school classes and activities pupils would like, so conducts a stratified sample survey of 50 pupils. How many pupils from each year should the school survey?

Answer:

Stage 1

First work out how many pupils are in the school

Stratified sampling example 2 step 1

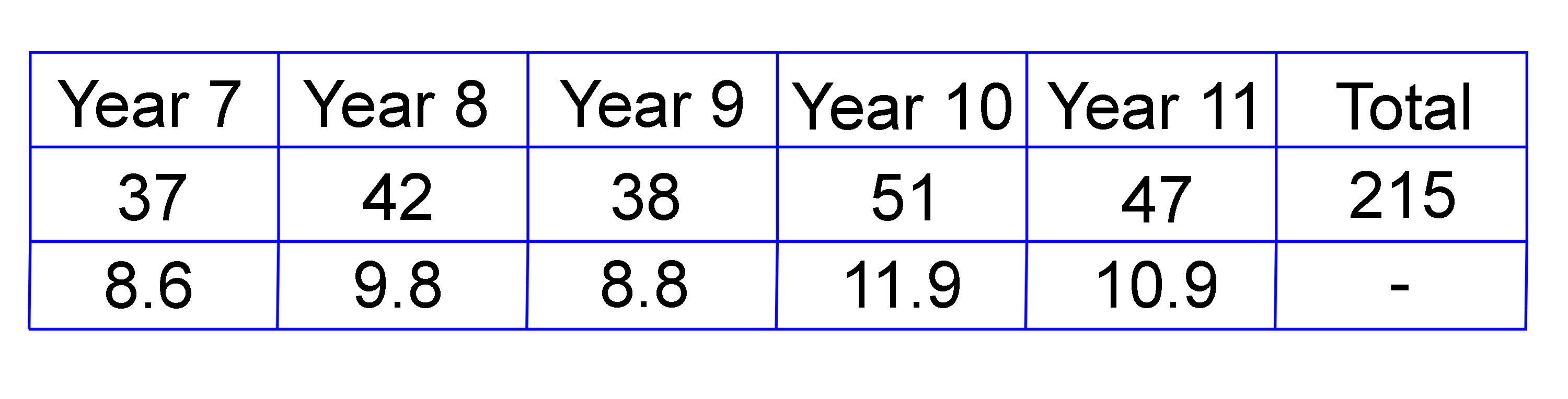
`37+42+38+51+47=215`

Stage 2

Work out what percentage of 215, 50 pupils represents:

`215=100%`

`50=x%`

(see our section on percentages)

`215/50=100/x`

Therefore `x=(100times50)/215`

`x=23.26%`

Stage 3

For each year work out 23.25% of the pupils.

Stratified sampling example 2 step 2

Year 7

23.26% of 37 would be:

`37=100%`

`x=23.26%`

(see our section on percentages)

`37/x=100/23.26`

Therefore `x=(37xx23.26)/100`

`x=8.6`

Repeat this process for each other year group:

Year 8 = 9.8

Year 9 = 8.8

Year 10 = 11.9

Year 11 = 10.9

Stratified sampling example 2 step 3

Stage 4

Round off the sample size to the nearest whole number for each strata and check what they total.

NOTE:

You will see the total once all the rounded sample sizes are added together: `9+10+9+12+11=51` is larger than the sample size of 50.

In this case what you have to do is reduce one of the sample sizes by 1 so that the sum of each strata sample matches the total sample size that was taken.

The most appropriate strata to reduce in this example would be the year 7 strata as it’s the lowest, although you would not lose marks if you were to choose another strata to reduce.

Answer:

Year 7 sample size = 8

Year 8 sample size = 10

Year 9 sample size = 9

Year 10 sample size = 12

Year 11 sample size = 11