Different refractive indices

The refractive index is a ratio but it actually means that:

Refractive index $(n)$ is the extent to which light is refracted (changes direction) when it enters a medium.

Also note that $n$ is a constant for a particular medium.

Some examples are:

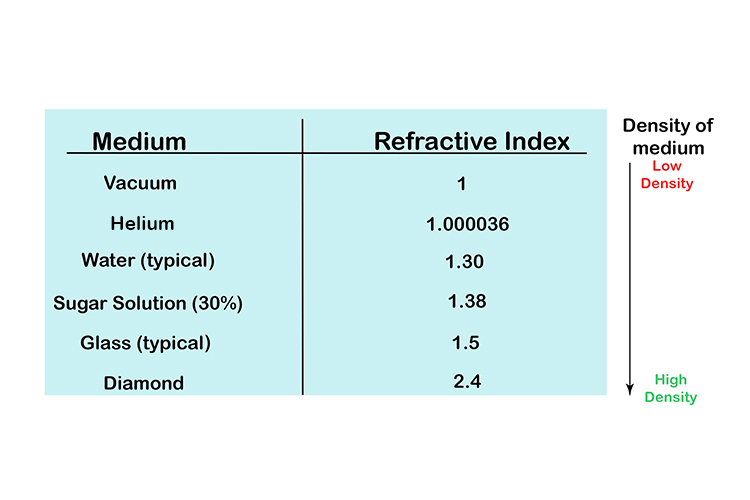
$Refractive index table.$

NOTE:	Low refractive index is low-density medium
	High refractive index is a high-density medium

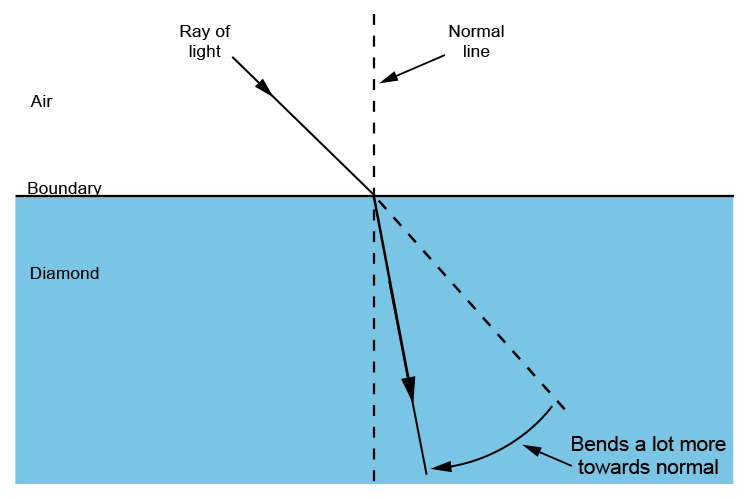
So a high-refractive index $(n)$ bends a lot more towards the normal line and a low refractive index $(n)$ bends very little towards the normal line.

HIGH N° $n$ = Much bend (HIGH bend) towards normal line
LOW N° $n$ = Little bend (LOW bend) towards the normal line

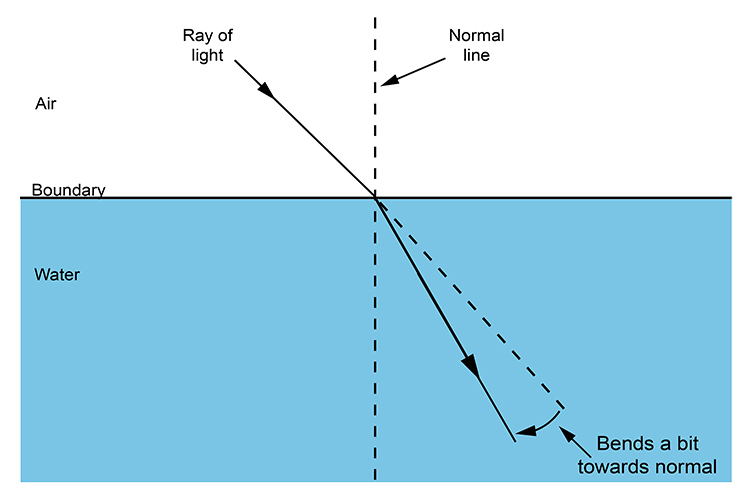
Refraction of air to water $n=1.3$

$Refraction of light travelling from air to water.$

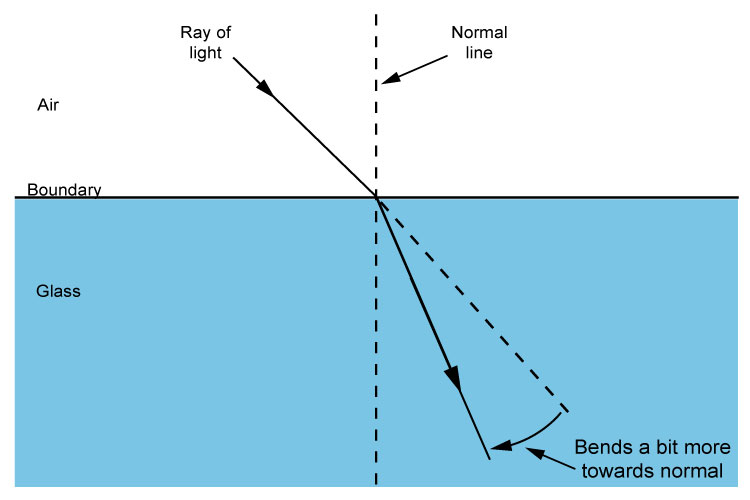
Refraction of air to glass $n=1.5$

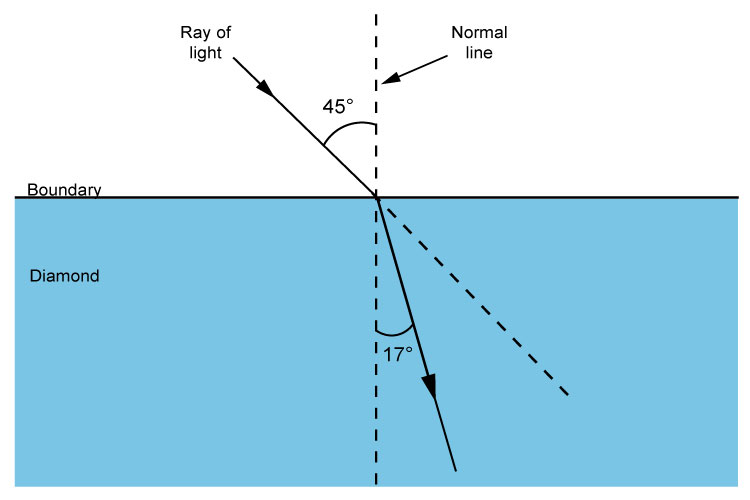
$Refraction of a ray of light as it travels from air into glass.$

Refraction of air to diamond $n=2.4$

$Refraction of a ray of light as it travels from air into diamond.$

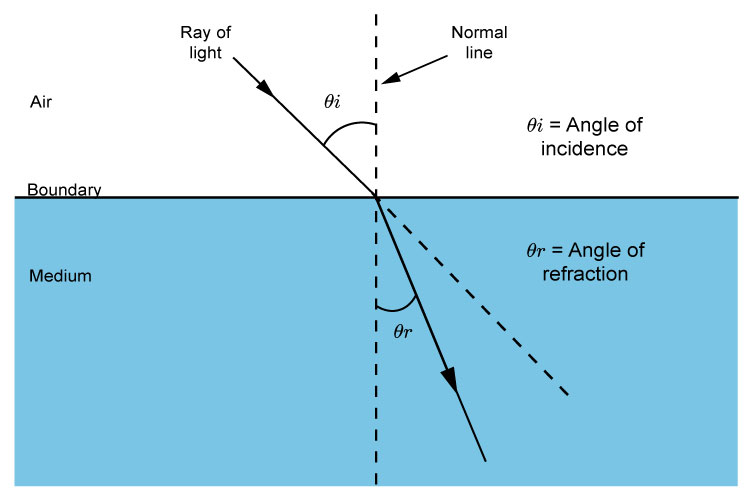
We can then use this information to find any angle of refraction when we know the value $n$ (refractive index) and angle of incidence $(theta\i)$ for any light ray travelling from air to a thicker medium.

$n=(sin\theta\i)/(sin\theta\r)$

$Angle of incidence and angle of refraction of a ray of light.$

Refraction of air to water

$n=1.3$ and $theta\i=45^circ$

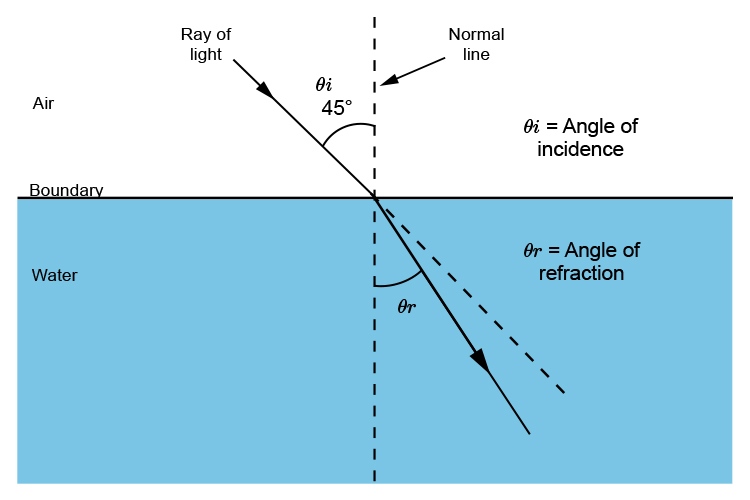
$Angle of incidence and angle of refraction of a ray of light travelling from air into water.$

$n=(sin\theta\i)/(sin\theta\r)$

$1.3=(sin45)/(sin\theta\r)$

Divide both sides by 1.3 and multiply both sides by $sin\theta\r$ to get $sin\theta\r$ on its own.

$sin\theta\r=(sin45)/1.3$

$sin\theta\r=0.7071/1.3=0.5439$

$\theta\r=sin^(-1)\0.5439$

$\theta\r=32.95^circ~~33^circ$

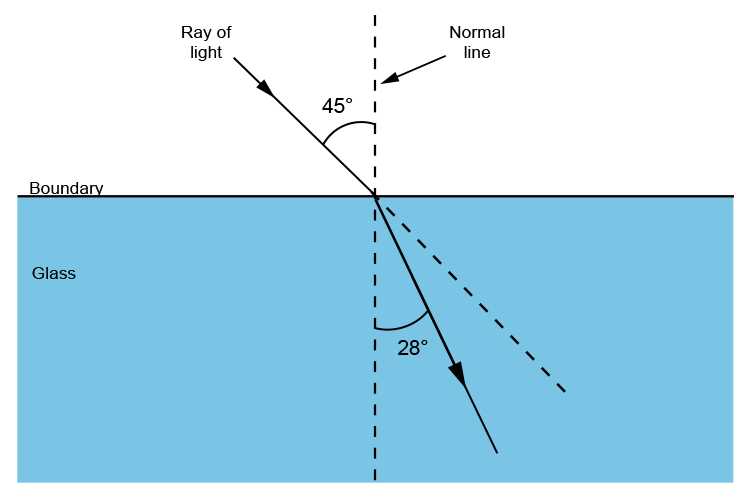
Refraction of air to glass

$n=1.5$ and $theta\i=45^circ$

$n=(sin\theta\i)/(sin\theta\r)$

$1.5=(sin45)/(sin\theta\r)$

Divide both sides by 1.5 and multiply both sides by $sin\theta\r$ to get:

$sin\theta\r=(sin45)/1.5$

$sin\theta\r=0.7071/1.5=0.4714$

$\theta\r=sin^(-1)\0.4714$

$\theta\r=28.12^circ~~28^circ$

Refraction of air to diamond

$n=2.4$ and $theta\i=45^circ$

$n=(sin\theta\i)/(sin\theta\r)$

$2.4=(sin45)/(sin\theta\r)$

Divide both sides by 2.4 and multiply both sides by $sin\theta\r$ to get:

$sin\theta\r=(sin45)/2.4$

$sin\theta\r=0.7071/2.4=0.295$

$\theta\r=sin^(-1)\0.295$

$\theta\r=17.16^circ~~17^circ$

Summary

When light shines at 45° towards a surface the angle from the normal line to the refracted ray is:

Water	=	33°
Glass	=	28°
Diamond	=	17°

Water 33°

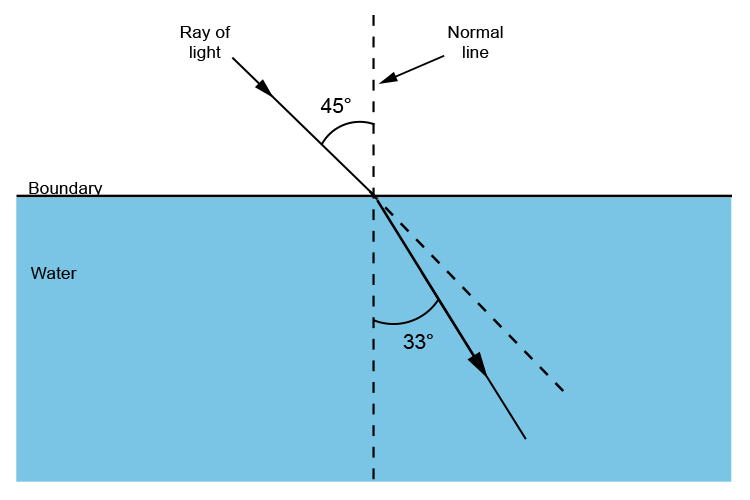
$Angle between normal line and refracted ray travelling into water.$

Glass 28°

$Angle between normal line and refracted ray travelling into glass.$

Diamond 17°

$Angle between normal line and refracted ray travelling into diamond.$