Snell's law in use
Snell's law can be simplified in use because in most text books the medium going in is air.
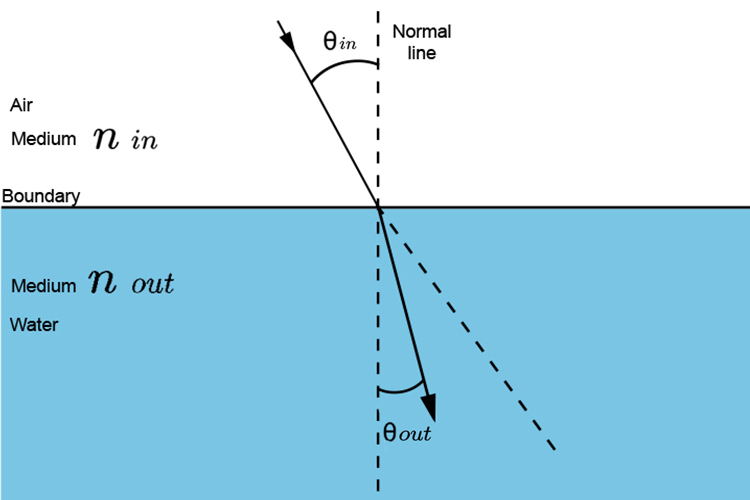
NOTE: how `theta` relates to the angle going in against the normal line is different to the angle coming out against the normal line.
We have learnt that Snell's law is
`(sin\ \i\n\ \theta)/(sin\ \out\ \theta)=(n\ \(out))/(n\ \(i\n))`
But the refractive index `n` of air for all practical purposes is one (1).
(In fact a vacuum is 1 and air is 1.0002926)
So most text books show Snell's law as being
`(sin\ \i\n\ \theta)/(sin\ \out\ \theta)=n\ \(out)`
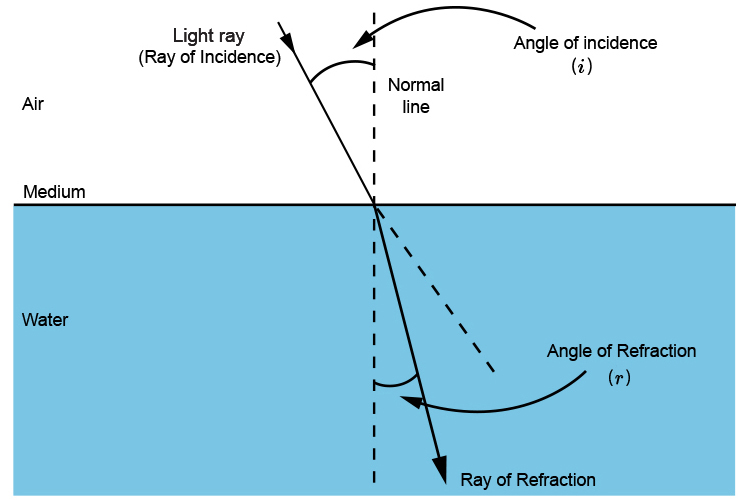
Angle of the incident = Angle of incidence `(i)`
Angle refracted = Angle of refraction `(r)`
Snell's law becomes:
`(sin\theta\i)/(sin\theta\r)=(n\ \m\e\d\i\u\m\ \w\a\t\e\r)/(n\ \m\e\d\i\u\m\ \a\i\r)`
Which becomes
`(sin\theta\i)/(sin\theta\r)=n/1`
Which becomes
`(sin\theta\i)/(sin\theta\r)=n` (refractive index of medium)
Summary
Most text books show Snell's law as
`n=(sin\ \i)/(sin\ \r)`




