Working out the critical angle

The critical angle (where $theta\ \o\u\t=90^circ$ ) can be worked out for different media using the following process.

Use

$sin\ \i\n\theta=1/(n(i\n))$

because

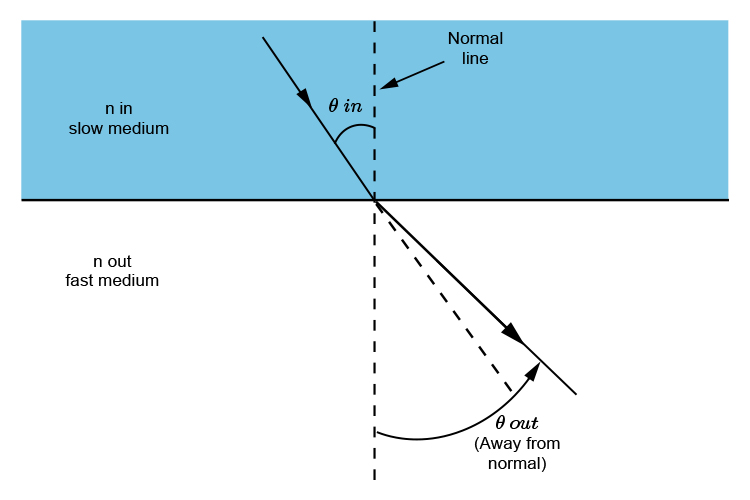
The angle of a ray of light travelling from a slow medium into a fast medium.

Remember FAST SOFA (slow in fast out away from the normal line)

and remember

$(sin\ \i\n\theta)/(sin\ \o\u\t\theta)=(n\ \(o\u\t))/(n\ \(i\n))$

but because $theta\ \o\u\t$ is at $90^circ$ $(sin90=1)$ and $n\ \o\u\t$ is 1 (for air) . . .

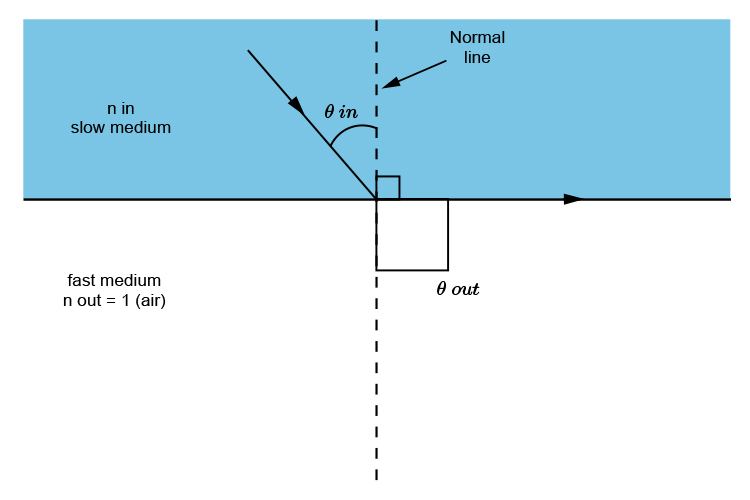
Critical angle of a ray of light travelling from a slow to a fast medium.

. . . the formula becomes

$(sin\ \i\n\theta)/1=1/(n\ \(i\n))$

and simplified

$sin\ \i\n\theta=1/(n\ \(i\n))$

Water to air

(water $n=1.3$ )

$sin\ \i\n\theta=1/1.3=0.769$

$theta=sin^-1\0.769$

$theta=50.26~~50^circ$

(Glass $n=1.5$ )

$sin\ \i\n\theta=1/1.5=0.66dot 6$

$theta=sin^-1\0.66dot 6$

$theta=41.81~~42^circ$

(Diamond $n=2.417$ )

$sin\ \i\n\theta=1/2.417=0.4137$

$theta=sin^-1\0.4137$

$theta=24.44~~24^circ$

The critical angle for