Completing the square – getting rid of the square (difficult)

When it isn’t obvious how to get rid of the square

Complete the following square:

Remember the above picture

NOTE:

1. The coefficient (or number) in front of the `x`  must be a 1
2. The next square must be ½ of the next term
3. Multiply out into all of the boxes

This method uses a visual model to solve a quadratic equation

For example:

`x^2+2x-8=0`

Quick sketch

Visually `x^2`  can look like an area of a table:

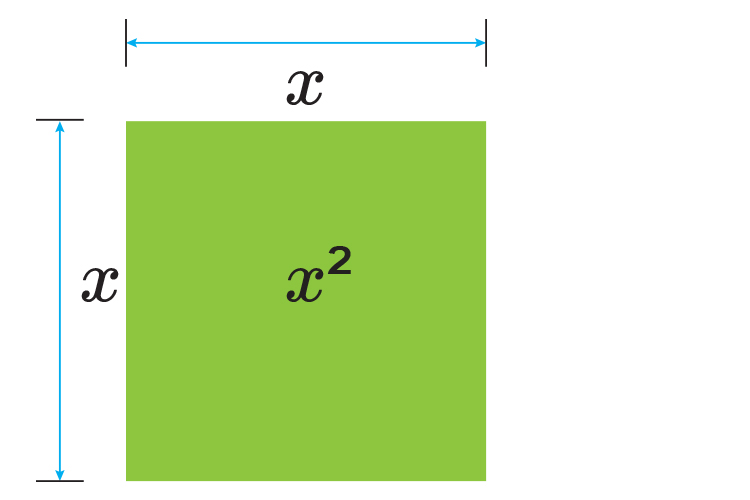
The `2x`  can be represented by:

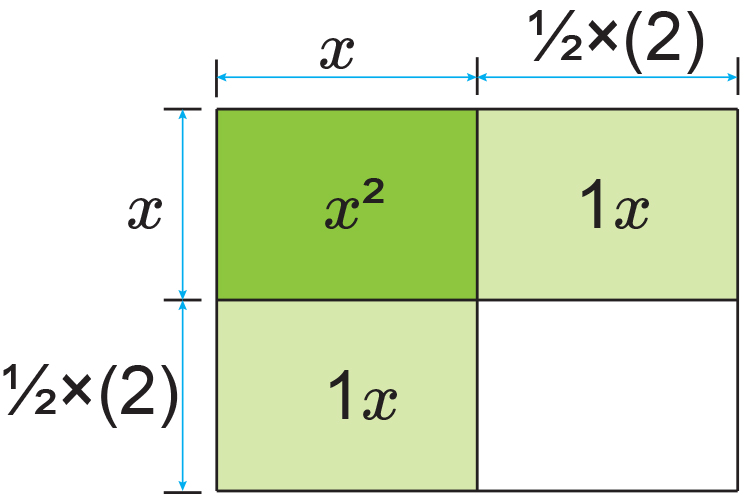
And this will therefore complete the last square as:

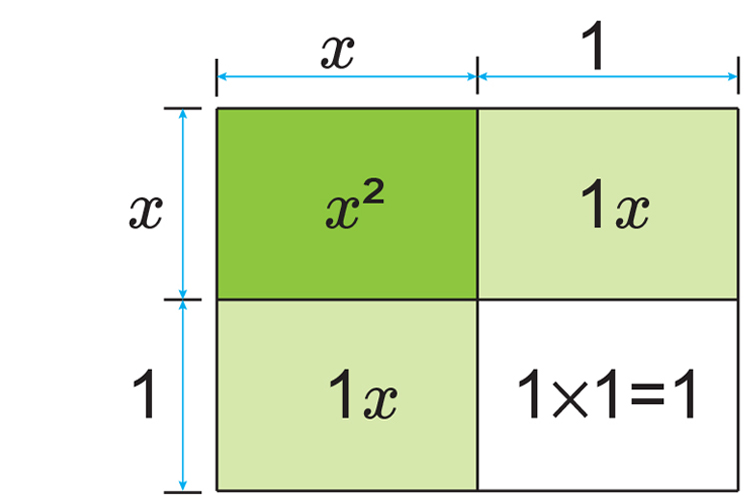
NOTE:

This is the same as `(x+1)^2`

At the moment if you add each area together you get:

`x^2+1x+1x+1times1`

`=x^2+2x+1`

Originally we had  `x^2+2x-8=0`

We now have         `x^2+2x+1=0`

Always plot this on a number line

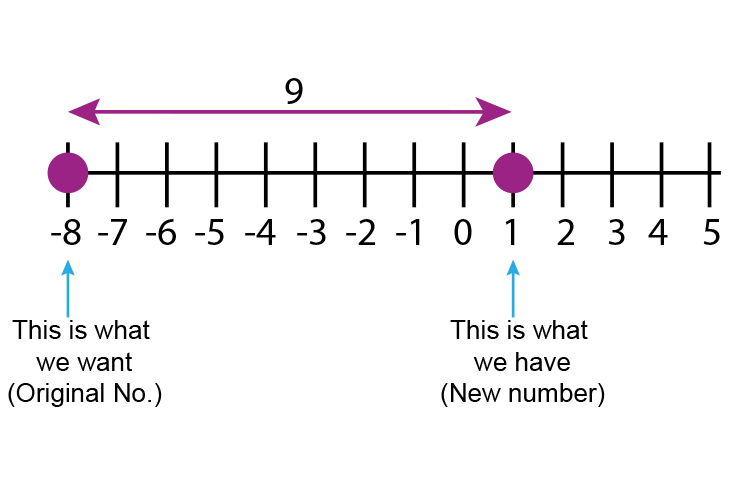
The number line will help you remember

Original number `-`  New number

`-8-1=-9`  (we need to `-9` )

So `x^2+2x-8=0`

Is the same as `(x+1)^2-9=0`

Which can now be solved

`(x+1)^2-9=0`

`(x+1)^2=9`

`x+1=+-sqrt9`

(Don't forget the root of anything can be `+`  or `-`)

`x+1=+-3`

`x=-1+-3`

`x=-1+3\ \ \ or\ \ \ x=-1-3`

`x=2\ \ \ or\ \ \ x=-4`

Now check

`x^2+2x-8=0`

If `x=2`            `2^2+2times2-8=0`  Which is correct

If `x=-4`     `(-4)^2+2times(-4)-8=0`

                           `16-8-8=0`  Which is correct

(If they don't add up to zero you can be assured that it is wrong)

Answer:

The roots of `x^2+2x-8=0`  are `x=2`  and `x=-4`