Completing the square - example 4

Complete the square $x^2+7x+10=0$

Quick sketch

Remember

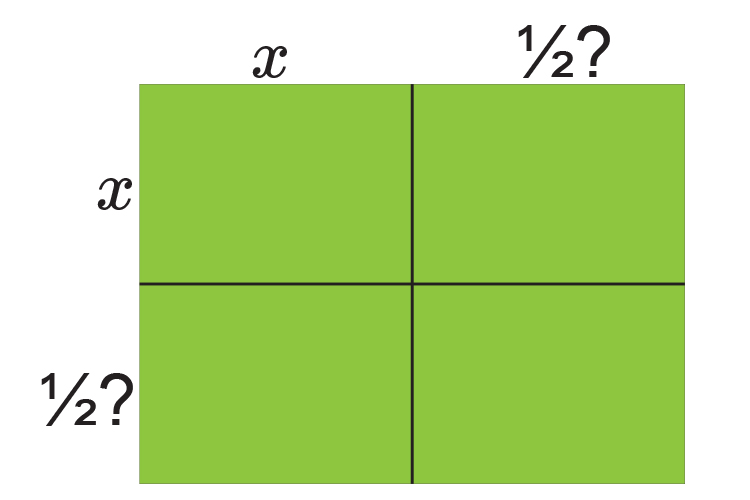
Complete the square and split the square into quarters using x square

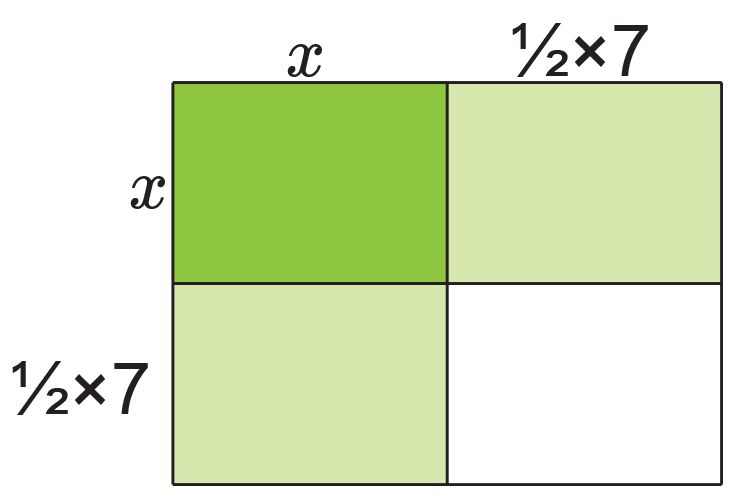
Fill the square in with the next term

Fill in

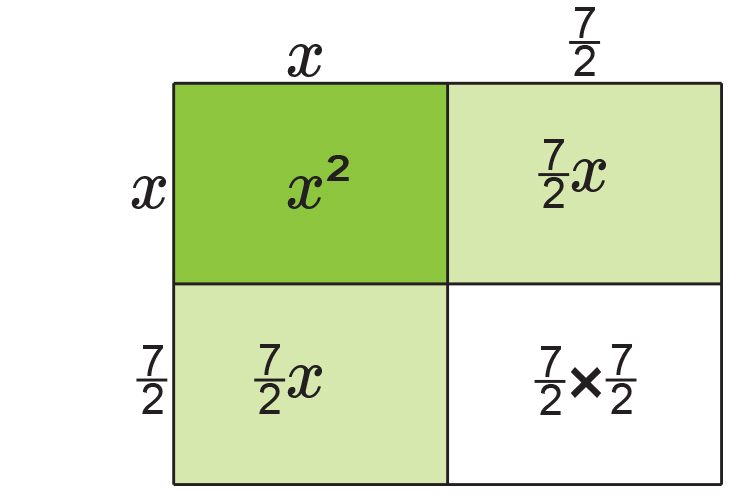
Fill in the table multiplying the y axis by the x axis

NOTE:

This is the same as $(x+7/2)^2$

If you add up each area you get:

$x^2+7/2x+7/2x+7/2times7/2$

$x^2+7x+49/4$

$x^2+7x+12\1/4$

Always plot this on a number line

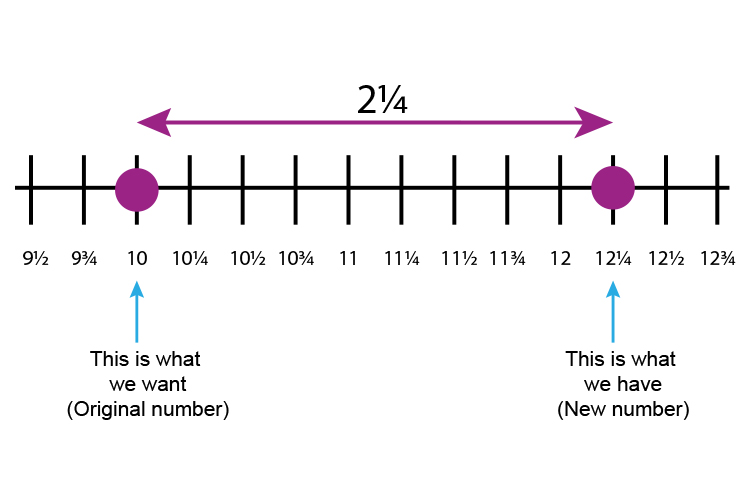
Use the number line to work out the difference between the original number and the new number

The number line will help you remember

Original number $-$ New number

$10-12\1/4=-2\1/4$

So $x^2+7x+10=0$

Is the same as

$(x+7/2)^2-2\1/4=0$

$(x+7/2)^2=2\1/4$

$x+7/2=+-sqrt(2\1/4)$

$x=-7/2+-sqrt(2\1/4)$

Using a calculator

$x=-3.5+-1.5$

$x=-3.5+1.5$ and $-3.5-1.5$

$x=-2$ and $-5$

Now check

$x^2+7x+10=0$

If $x=-2$ $(-2)^2+7times(-2)+10=0$

$+4-14+10=0$ Which is correct

If $x=-5$ $(-5)^2+7times(-5)+10=0$

$25-35+10=0$ Which is correct

Answer:

The roots of $x^2+7x+10=0$ are $x=-2$ and $x=-5$

NOTE:

This example has also been used in factorising quadratics (easy) and quadratic formula examples to show that the roots $-2$ and $-5$ can be found using any of these methods.