Fun with simultaneous equations
Example 1
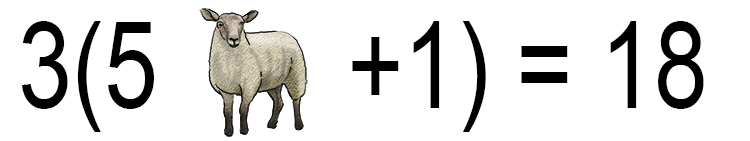
What is a sheep worth?
The way to tackle this question is to substitute the sheep for a letter. So the equation above becomes:
`3(5x+1)=18`
Multiply the `3` into the brackets:
`3times5x+3times1=18`
`15x+3=18`
Subtract `3` from both sides to help get `x` on its own:
`15x+cancel(3)-cancel(3)=18-3`
`15x=15`
Divide both sides by `15` to get `x` on its own:
`(cancel(15)x)/cancel(15)=15/15`
`x=15/15`
`x=1`
Answer: The sheep is worth 1.
Example 2
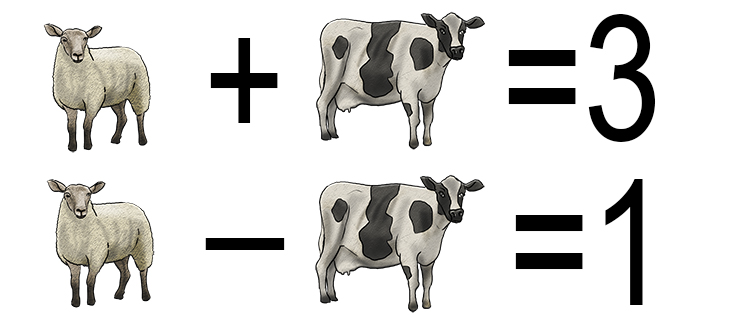
What is a sheep worth and what is a cow worth?
The way to tackle this question is to substitute both the sheep and the cow with letters. So the equations become:
`s+c=3` ...equation 1
`s-c=1` ...equation 2
Take the first equation and subtract `s` from both sides to get `c` on its own:
`s-s+c=3-s`
`c=3-s`
Now substitute `c` into equation 2:
`s-(3-s)=1`
There is a 1 behind the minus sign but mathematicians usually hide it, but in this case we will put it back:
`s-1(3-s)=1`
Multiply the `-1` into the brackets:
`s-3+s=1`
Add the two `s`'s:
`-3+2s=1`
Add `3` to both sides to help get `s` on its own:
`-cancel(3)+cancel(3)+2s=1+3`
`2s=4`
Divide both sides by `2` to get `s` on its own:
`(cancel(2)s)/cancel(2)=4/2`
`s=4/2`
`s=2`
Now we know that `s=2` we can plug that back into equation 1 or 2 to get the value of `c`.
Try equation 1:
`s+c=3`
`2+c=3`
Take 2 from both sides to get `c` on its own:
`cancel(2)-cancel(2)+c=3-2`
`c=1`
Answer: The sheep is worth 2 and the cow is worth 1.
Example 3
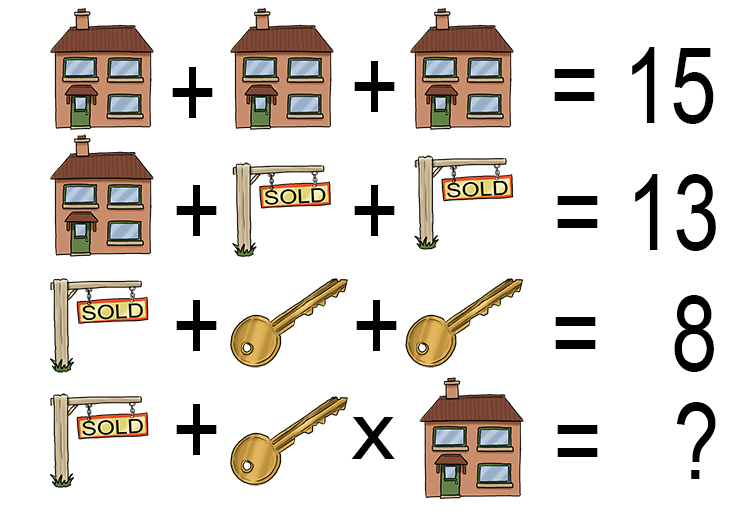
What is the value of the question mark?
The way we tackle this question is to substitute each symbol for a letter i.e. sign = `s`, house = `h`, key = `k`.
`h+h+h=15` ...equation 1
`h+s+s=13` ...equation 2
`s+k+k=8` ...equation 3
`s+ktimesh=?` ...equation 4
Immediately we can see that that equation 1 is the easiest to tackle:
`h+h+h=15`
Add the `h`'s together and we get:
`3h=15`
Divide both sides by `3` to get `h` on its own:
`(cancel(3)h)/cancel(3)=15/3`
`h=15/3`
`h=5`
Substitute `h=5` into equation 2 and we get:
`h+s+s=13`
`5+s+s=13`
`5+2s=13`
Minus `5` from both sides to help get `s` on its own:
`cancel(5)-cancel(5)+2s=13-5`
`2s=8`
Divide both sides by `2` to get s on its own:
`(cancel(2)s)/cancel(2)=8/2`
`s=8/2`
`s=4`
Substitute `s=4` into equation 3 and we get:
`s+k+k=8`
`4+k+k=8`
`4+2k=8`
Minus `4` from both sides to help get `k` on its own:
`cancel(4)-cancel(4)+2k=8-4`
`2k=4`
Divide both sides by `2` to get `k` on its own:
`(cancel(2)k)/cancel(2)=4/2`
`k=4/2`
`k=2`
Substitute values of `h=5`, `s=4` and `k=2` into equation 4 and we get:
`s+ktimesh=?`
`4+2times5=?`
`4+10=?`
`?=14`
Answer: The value of the question mark is `14`.
Example 4
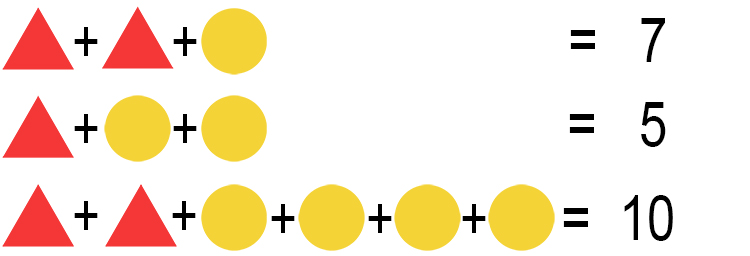
Find the value of a triangle and a circle.
The way to tackle this problem is to substitute each symbols for a letter i.e. triangle`=x` and circle`= y`.
`x+x+y=7` ...equation 1
`x+y+y=5` ...equation 2
`x+x+y+y+y+y=10` ...equation 3
Which then becomes:
`2x+y=7` ... equation 1
`x+2y=5` ...equation 2
`2x+4y=10` ...equation 3
We can see that equations 1 and 3 both have a `2x` in them.
Tackling equation 1:
`2x+y=7`
Take `y` from either side to get `2x` on its own:
`2x+cancel(y)-cancel(y)=7-y`
`2x=7-y`
Substitute this into equation 3:
`2x+4y=10`
`7-y+4y=10`
`7+3y=10`
Take `7` from both sides to help get `y` on its own:
`cancel(7)-cancel(7)+3y=10-7`
`3y=3`
Divide both sides by `3` to get `y` on its own:
`(cancel(3)y)/cancel(3)=3/3`
`y=3/3`
`y=1`
Substitute `y=1` into equation 1 and we get:
`2x+y=7`
`2x+1=7`
Take `1` from both sides to help get `x` on its own:
`2x+cancel(1)-cancel(1)=7-1`
`2x=6`
Divide both sides by `2` to get `x` on its own:
`(cancel(2)x)/cancel(2)=6/2`
Answer:
So `y=1` and `x=3`.
or circle`=1` and triangle `=3`.
Note: We didn't even need to use equation 2.




