Graphical simultaneous equations

We know

Simultaneous equations `=` two equations with two unknowns

and

Graphical = Draw the lines on the graph.

The only additional item you need to know is:

The meeting place of the equations is the solution

When they meet they find the solution.

(The point where the two lines intersect on a graph is the solution).

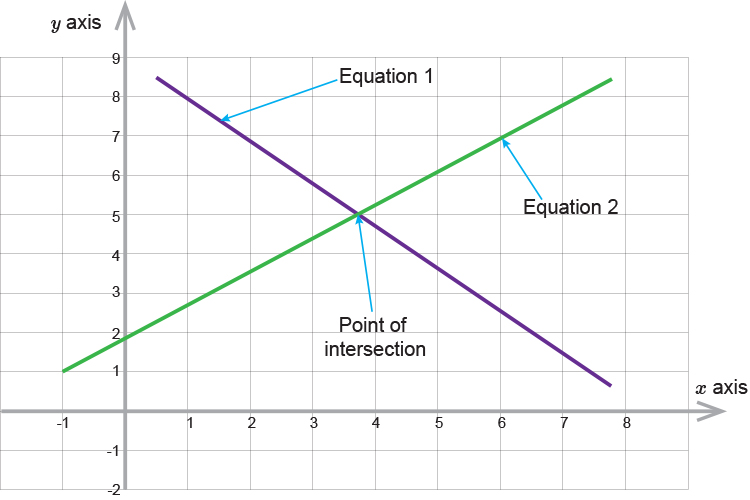
Both equations plotted on a graph, the meeting place is the solution

If you find where `x` and `y` intersect on a graph that is the solution.

NOTE:

To continue you must understand our section on formula for a straight line.

That is:

Always make `y` the subject of the formula
Formula of a straight line is `y=mx+c`
Plot `x` and `y` for given values of `x`

Example 1

Plot the graphs of the following equations and find their solution by finding the point of intersection.

`2x+3y=6`

`4x-6y=-4`

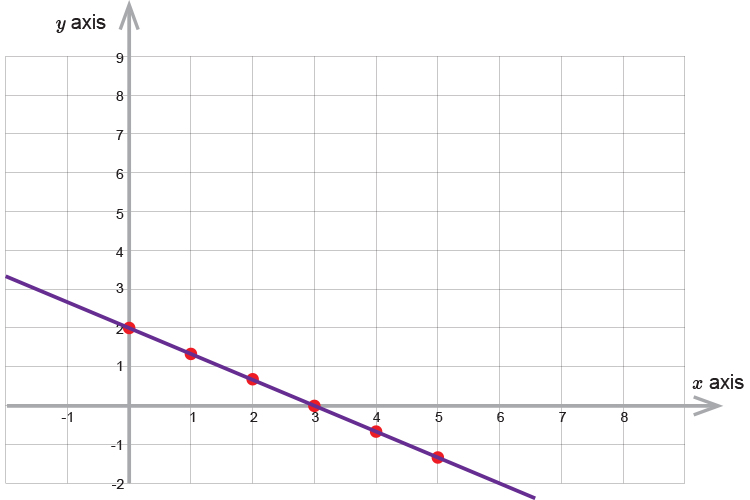
So first plot the graph of the following equation:

`2x+3y=6`

Subtract `2x` from both sides to get `y` on its own.

`2x-2x+3y=6-2x`

`3y=6-2x`

Divide both sides by 3 to get `y` on its own.

`y=6/3-(2x)/3`

`y=2-2/3x`

Lets plot some points on the graph

If `x=5`	then	`y=2-2/3(5)`	`=-1.33`
`x=4`	then	`y=2-2/3(4)`	`=-0.66`
`x=3`	then	`y=2-2/3(3)`	`=0`
`x=2`	then	`y=2-2/3(2)`	`=0.67`
`x=1`	then	`y=2-2/3(1)`	`=1.33`
`x=0`	then	`y=2-2/3(0)`	`=2`

First plot the first equation on the graph following the x and y axis

Now lets add to the graph the equation:

`4x-6y=-4`

Subtract `4x` from both sides to get `y` on its own.

`-4x+4x-6y=-4-4x`

`-6y=-4-4x`

Divide both sides by `-6` to get `y` on its own.

`y=(-4)/(-6)-(4x)/-6`

`y=2/3+(2x)/3`

Lets plot some points on the graph

If `x=5`	then	`y=2/3+(2times5)/3`	`=2/3+10/3=12/3`	`=4`
`x=4`	then	`y=2/3+(2times4)/3`	`=2/3+8/3=10/3`	`=3\1/3`
`x=3`	then	`y=2/3+(2times3)/3`	`=2/3+6/3=8/3`	`=2\2/3`
`x=2`	then	`y=2/3+(2times2)/3`	`=2/3+4/3=6/3`	`=2`
`x=1`	then	`y=2/3+(2times1)/3`	`=2/3+2/3=4/3`	`=1\1/3`
`x=0`	then	`y=2/3+(2times0)/3`		`=2/3`

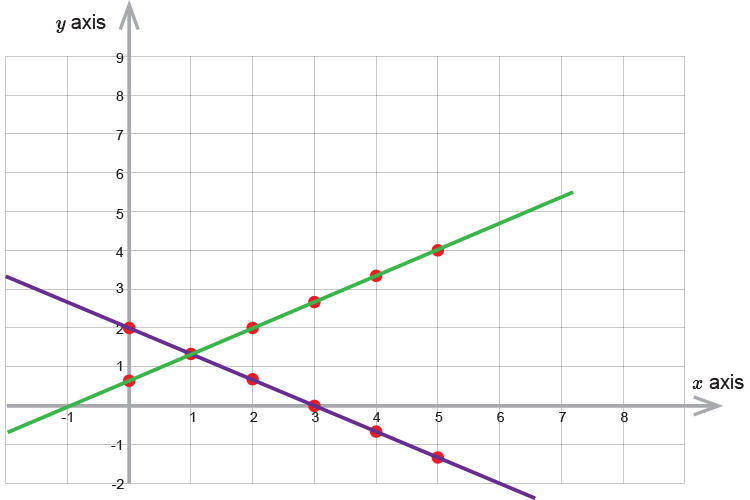
Then plot the second equation

We can see from the graph that the two lines intersect (and therefore the solution) at:

`x=1` `y=1\1/3`

Example 2

Plot the graphs of the following equations and find their solution by finding the point of intersection.

`y=x+3`

`x+y=7`

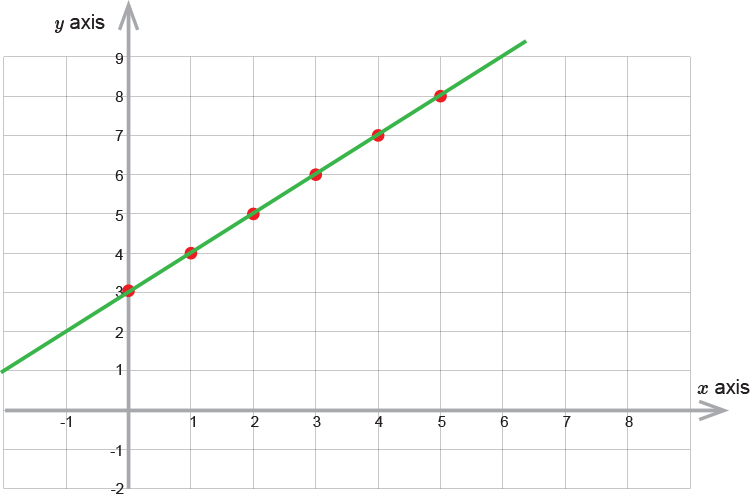
So first plot the following equation on a graph.

`y=x+3`

Lets put some points on the graph

If `x=5`	then	`y=5+3`	`=8`
`x=4`	then	`y=4+3`	`=7`
`x=3`	then	`y=3+3`	`=6`
`x=2`	then	`y=2+3`	`=5`
`x=1`	then	`y=1+3`	`=4`
`x=0`	then	`y=0+3`	`=3`

Plot the first equation example 2

Now lets add to the graph the equation:

`x+y=7`

Subtract `x` from both sides to get `y` on its own

`x-x+y=7-x`

`y=7-x`

Lets plot some points on the graph

If `x=5`	then	`y=7-5`	`=2`
`x=4`	then	`y=7-4`	`=3`
`x=3`	then	`y=7-3`	`=4`
`x=2`	then	`y=7-2`	`=5`
`x=1`	then	`y=7-1`	`=6`
`x=0`	then	`y=7-0`	`=7`

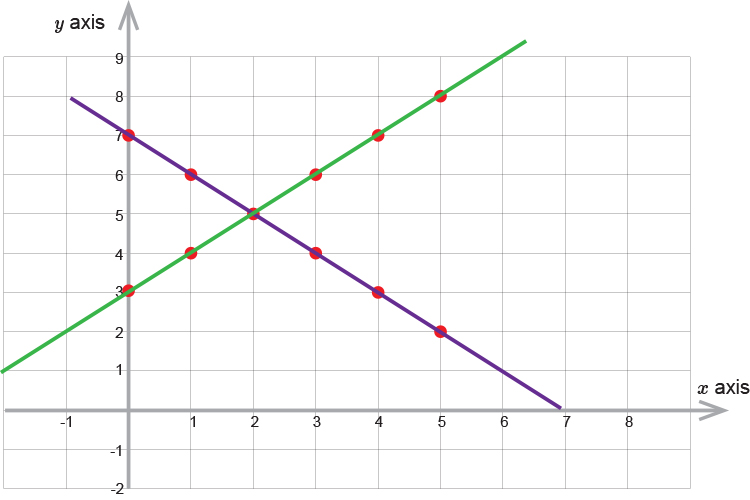
Plot the second equation and find where both intersect example 2

We can see from the graph that the two line intersect (and therefore the solution) at:

`x=2` `y=5`

Example 3

Plot the graphs of the following equations and find their solution by finding the point of intersection.

`2x+2y=6`

`4x-6y=12`

So first plot the graph of the following equation.

`2x+2y=6`

Subtract `2x` from both sides to get `y` on its own

`2x-2x+2y=6-2x`

`2y=6-2x`

Divide both sides by 2 to get `y` on its own

`(2y)/2=6/2-(2x)/2`

`y=3-x`

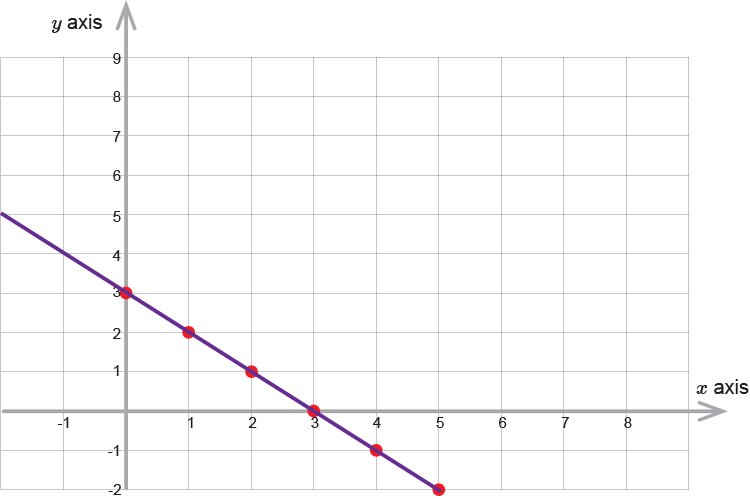
Lets put some points on the graph

If `x=5`	then	`y=3-5`	`=-2`
`x=4`	then	`y=3-4`	`=-1`
`x=3`	then	`y=3-3`	`=0`
`x=2`	then	`y=3-2`	`=1`
`x=1`	then	`y=3-1`	`=2`
`x=0`	then	`y=3-0`	`=3`

Plot the first equation example 3

Now lets add to the graph the equation:

`4x-6y=12`

Subtract `4x` from both sides to get `y` on its own

`4x-4x-6y=12-4x`

`-6y=12-4x`

Divide both sides by `-6` to get `y` on its own.

`(-6y)/(-6)=12/-6-(4x)/-6`

`y=-2+2/3x`

Lets plot some points on the graph

If	`x=5`	then	`y=-2+2/3times5`	`=-2+10/3=-2+3\1/3`	`=1\1/3`

	`x=4`	then	`y=-2+2/3times4`	`=-2+8/3=-2+2\2/3`	`=2/3`

	`x=3`	then	`y=-2+2/3times3`	`=-2+6/3=-2+2`	`=0`

	`x=2`	then	`y=-2+2/3times2`	`=-2+4/3=-2+1\1/3`	`=-2/3`

	`x=1`	then	`y=-2+2/3times1`	`=-2+2/3=-2+2/3`	`=-1\1/3`

	`x=0`	then	`y=-2+2/3times0`		`=-2`

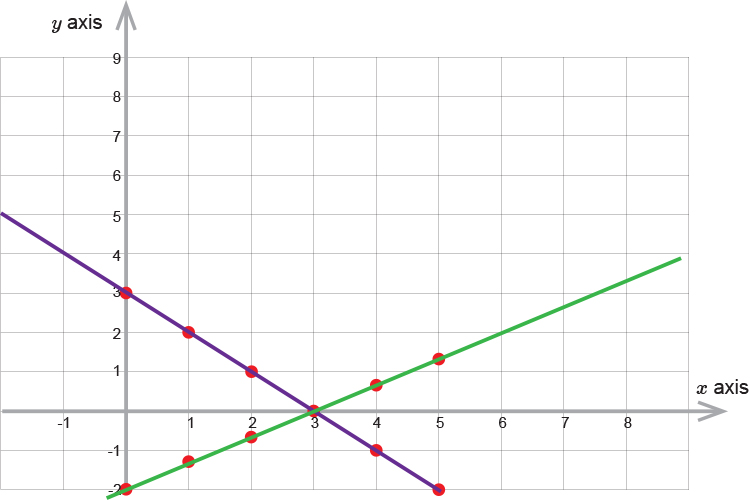
Plot the second equation and find where both intersect to find the solution example 3

We can see from the graph that the two line intersect (and therefore the solution) at:

`x=3` `y=0`