Simultaneous equations - the substitution method
To solve two equations with two unknowns. Substitute the `y` in one equation into the `y` of the other.
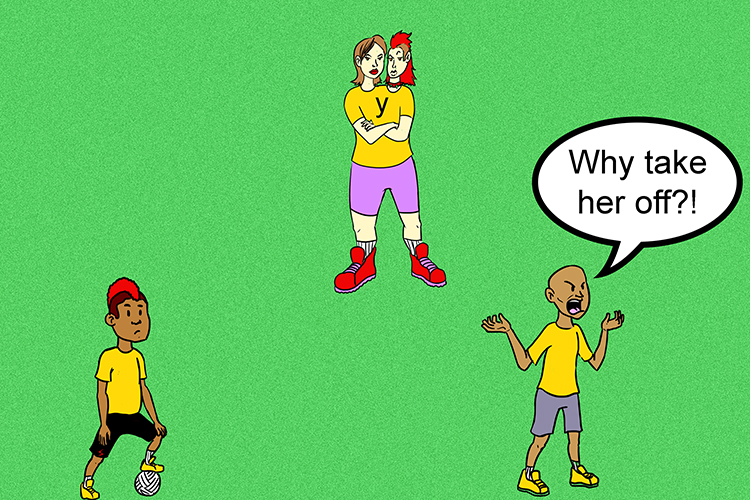
Substitute the `y`
Example 1
Solve `x+y=24` ..................... equation 1
`2x-y=-6` ................ equation 2
Take the first equation
`x+y=24` ...................... equation 1
Subtract `x` from both sides to get `y` on its own.
`-x+x+y=24-x`
`y=24-x`
Now substitute this into equation 2:
`2x-y=-6`
`2x-1times(24-x)=-6`
`2x-24+x=-6`
`3x-24=-6`
Add 24 to both sides to get `x` on its own.
`3x-24+24=-6+24`
`3x=18`
Divide both sides by 3 to get `x` on its own
`(3x)/3=18/3`
`x=6`
Now that `x=6` we can plug this into either equation 1 or 2 to get the value of `y`
Try `x+y=24`
`6+y=24`
Subtract 6 from both sides to get the value of `y`
`-6+6+y=24-6`
`y=18`
Answer:
Solution is `x=6` `y=18`
Example 2
Solve `2x+3y=6` ...................... equation 1
`4x-6y=-4` ................ equation 2
NOTE:
This is the same question as simultaneous equation graphical.
Take the first equation
`2x+3y=6` ...................... equation 1
Subtract `2x` from both sides to get `y` on its own.
`2x-2x+3y=6-2x`
`3y=6-2x`
Divide both sides by 3 to get `y` on its own.
`y=6/3-(2x)/3`
`y=2-2/3x`
Now substitute this into equation 2:
`4x-6y=-4`
`4x-6(2-2/3x)=-4`
`4x-6times2-6times(-2/3)x=-4`
`4x-12+12/3x=-4`
`4x-12+4x=-4`
`8x-12=-4`
Add 12 to both sides to get `x` on its own.
`12+8x-12=-4+12`
`8x=8`
Divide both sides by 8 to get `x` on its own
`x=8/8`
`x=1`
Now that `x=1` we can plug this into either original equation 1 or 2 to get the value of `y`
Try `4x-6y=-4`
`4times1-6y=-4`
`4-6y=-4`
Subtract `4` from both sides to get the value of `y`
`4-4-6y=-4-4`
`-6y=-8`
Divide both sides by `-6` to get the value of `y`
`(-6y)/-6=(-8)/-6`
`y=8/6`
`y=4/3`
`y=1\1/3`
Answer:
Solution is `x=1` `y=1\1/3`
Example 3
Solve `y=x+3` ............... equation 1
`x+y=7` ................ equation 2
NOTE:
This is the same question as simultaneous equation graphical.
Take the first equation
`y=x+3` ................ equation 1
and substitute it into equation 2.
`x+y=7`
`x+(x+3)=7`
`2x+3=7`
Subtract `3` from both sides to get `y` on its own.
`-3+2x+3=7-3`
`2x=7-3`
`2x=4`
Divide both sides by 2 to get `x` on its own.
`(2x)/2=4/2`
`x=4/2`
`x=2`
Now that `x=2` we can plug this into either equation 1 or 2 to get the value of `y`
Try `x+y=7`
`2+y=7`
Subtract `2` from both sides to get a value of `y`
`2-2+y=7-2`
`y=7-2`
`y=5`
Answer:
Solution is `x=2` `y=5`
Example 4
Solve `2x+2y=6` .................. equation 1
`4x-6y=12` ................ equation 2
NOTE:
This is the same question as simultaneous equation graphical.
Take the first equation
`2x+2y=6` .................. equation 1
Subtract `2x` from both sides to get `y` on its own
`-2x+2x+2y=6-2x`
`2y=6-2x`
Divide both sides by 2 to get `y` on its own.
`(2y)/2=6/2-(2x)/2`
`y=3-x`
Now substitute this into equation 2
`4x-6y=12`
`4x-6(3-x)=12`
`4x-6times3-(6)times(-x)=12`
`4x-6times3-(-6x)=12`
`4x-18+6x=12`
`10x-18=12`
Add 18 to both sides to get `x` on its own.
`10x-18+18=12+18`
`10x=12+18`
`10x=30`
Divide both sides by 10 to get `x` on its own.
`(10x)/10=30/10`
`x=30/10`
`x=3`
Now that `x=3` we can plug this into either original equation 1 or 2 to get the value of `y`
Try `4x-6y=12`
`4times(3)-6y=12`
`12-6y=12`
Subtract `12` from both sides to get a value of `y`
`12-12-6y=12-12`
`-6y=12-12`
`-6y=0`
Divide both sides by `-6` to get `y` on its own.
`(-6y)/-6=0/-6`
`y=0/-6`
`y=0`
Answer:
Solution is `x=3` `y=0`




