turning point of a parabola (method 1)

In an exam you might be asked to find the turning point of a parabola.

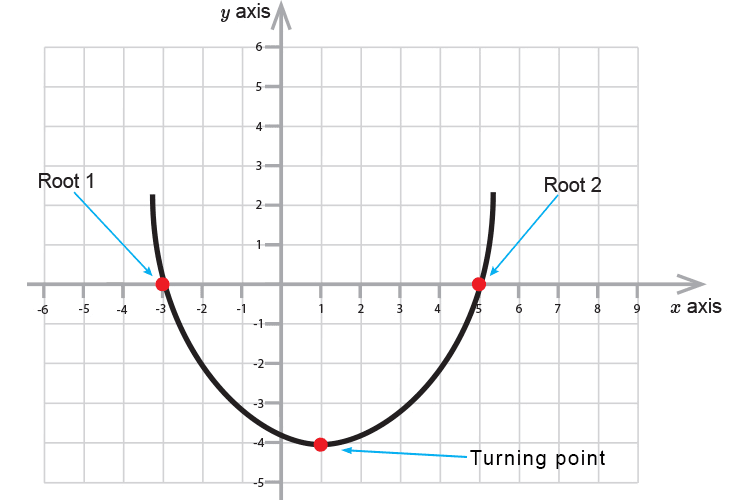
The turning point of a parabola is half way between the roots. So one way to find the turning point is to first find the roots. 

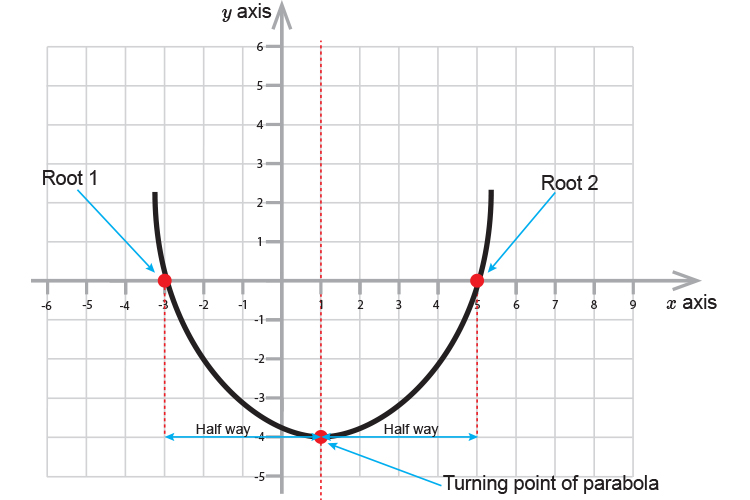
In the last few pages we at Mammoth Memory have given you four ways to find the roots i.e.

1. Draw the graph and see where the parabola passes the X axis.
2. Complete the square.
3. Use the quadratic formula equation.
4. Factorise the quadratic.

Once you have found the roots you can divide the distance apart on the X axis by half and this will give you the coordinate of `x` on the turning point. 

Now put that value of `x` back into the quadratic and you will be able to find the coordinate of `y` on the turning point.

Let's give you an example where we find the roots by drawing the graph and visually seeing where the roots pass the X axis at `y=0`.

Let's find the roots of:

`x^2-6x+8=y`

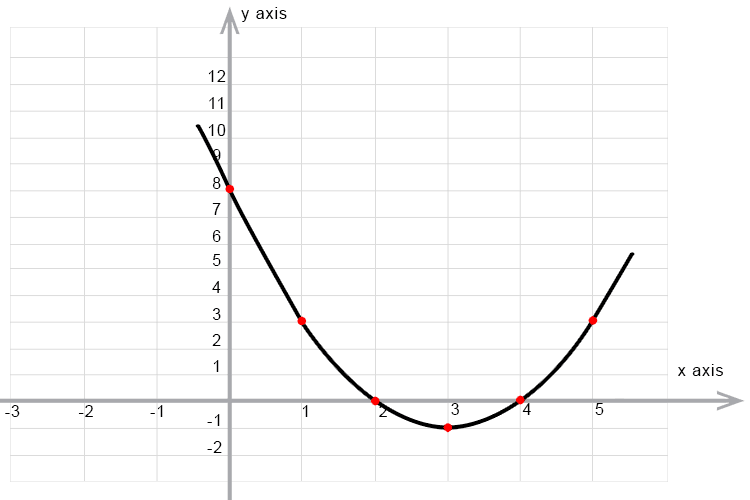
Let's complete a quick sketch:

`x=5`   `y=5^2-6`x`5+8=25-30+8=3`

`x=4`   `y=4^2-6`x`4+8=16-24+8=0`

`x=3`   `y=3^2-6`x`3+8=9-18+8=-1`

`x=2`   `y=2^2-6`x`2+8=4-12+8=0`

`x=1`   `y=1^2-6`x`1+8=1-6+8=3`

`x=0`   `y=0^2-6`x`0+8=0-0+8=8`

The turning point is half way between the roots.

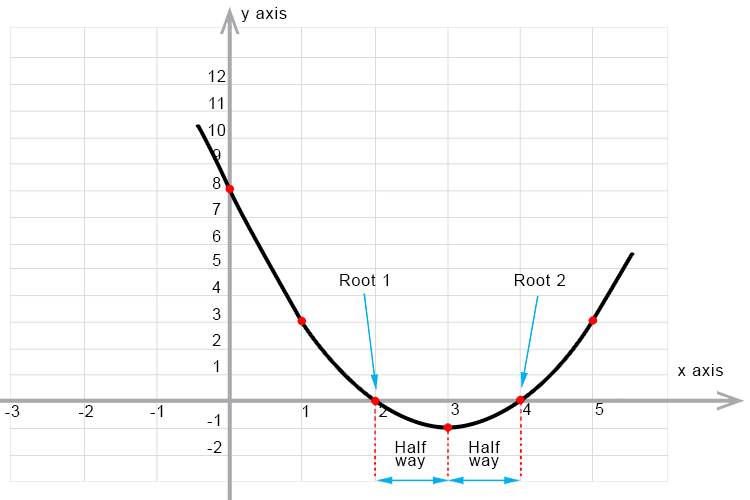
We can see that half way between these roots is `x=3`

Now put the value of `x=3` back into the quadratic equation

`x^2-6x+8=y`

`3^2-6`x`3+8=y`

`9-18+8=y`

`y=-1`

The turning point occurs at:

`x=3` and `y=-1`

or (3,-1)